Системы счисления. Задание: автомат

Бит чётности – это дополнительный контрольный бит,
который добавляется к двоичному коду так,
чтобы количество единиц в полученном двоичном коде стало чётным.
Если в исходном коде было чётное количество единиц, дописывается 0;
если нечётное – дописывается 1.

ТИП-1

ТИП №1
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 31.
В ответе это число запишите в десятичной системе счисления.

Алгоритм решения.
Перевести число в Р=2
это число R → 3110 = 111112
Отсекаем два последних разряда. → 111 → это число N ( его обрабатывать бессмысленно), поэтому
к этому числу прибавляем 1. → 1000 → это тоже число N, которое мы будем обрабатывать по алгоритму.
Проверяем по алгоритму.
1000 → 10001
10001 → 100010 =34 → это число R оно больше 31,
Получили это число обработкой числа N=1000 (п.4a) и проверили по алгоритму
Ответ: 10002 = 810

Задача №1.
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если нечётное.
3) К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 103.
В ответе это число запишите в десятичной системе.

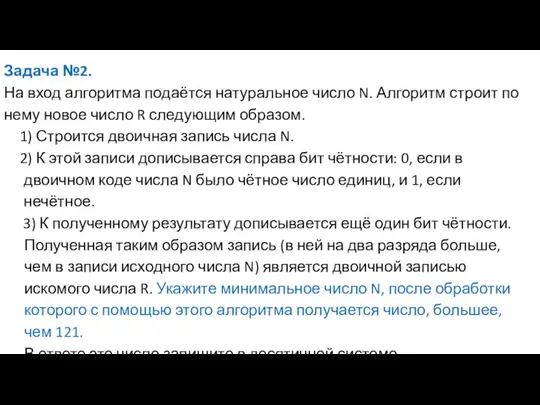
Задача №2.
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если нечётное.
3) К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 121.
В ответе это число запишите в десятичной системе.

ТИП-2

ТИП №2
На вход алгоритма подаётся натуральное число N.
Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа).
Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, большее, чем 116, которое может быть получено в результате работы этого алгоритма.
В ответе это число запишите в десятичной системе.

Алгоритм решения.
Перевести число в Р=2
11610 = 11101002 → это число R
Отсекаем два последних разряда. → 11101 → это число N, при обработке которого по алгоритму мы получим 116, т.е. R, а нам надо число большее, чем 116.
К этому числу прибавляем 1. → 11110 → это число N, которое мы будем проверять, даст ли оно при обработке по алгоритму число R >116
Проверяем по алгоритму.
11110 → 111100
б) 111100 → 1111000 → это число R, которое получилось в результате обработки по алгоритму, и оно >116.
Ответ: 11110002 = 12010

ЕЩЁ одно объяснение той же задачи

Операция над числом выполняется два раза, значит к числу N добавляется два разряда.
Определим, что может быть окончанием числа R, то есть разберем два последних разряда.
Если изначально сумма разрядов число нечётное.
— например 10101, то сначала оно будет преобразовано
а) в 101011 (добавили 1), т.к. сумма разрядов равна 3;
б) затем в 1010110 (добавили 0), т.к. сумма разрядов равна 4.
Если сумма разрядов число чётное.
— например 10001, то сначала оно будет преобразовано
а) в 110000 (добавили 0), т.к. сумма разрядов равна 2;
б) затем в 1100000 (добавили 0), т.к. сумма разрядов не изменилась.

Теперь рассмотрим число 116. 11610 = 11101002
При этом 11011002 — это число R,
а исходное число N на два разряда меньше, то есть 111012.
Если мы выполним алгоритм для этого числа N (111012), то у нас получится, 11101002 это само число 116.
Поэтому берем N на единицу больше, то есть 111102.
Проверяем.
— 11110 — сумма разрядов чётная, добавляем 0 в конец → 111100
б)— 111100— сумма разрядов четная, добавляем 0 в конец → 1111000
То есть наименьшее число R > 116 — это 1111000 в двоичной или
120 в десятичной.
Ответ:R= 120

Задача №3.
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если нечётное.
3) К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, большее 96, которое может быть получено в результате работы этого алгоритма.
В ответе это число запишите в десятичной системе.

Задача №4.
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если нечётное.
3) К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, большее 130, которое может быть получено в результате работы этого алгоритма.
В ответе это число запишите в десятичной системе.

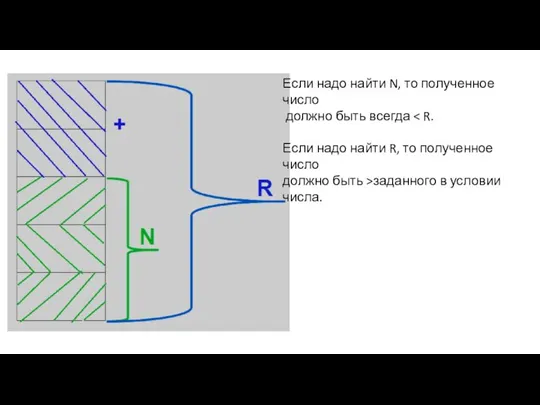
Если надо найти N, то полученное число
должно быть всегда < R.
Если надо найти R, то полученное число
должно быть >заданного в условии числа.

ТИП-3

Автомат обрабатывает натуральное число N по следующему алгоритму:
1. Строится двоичная запись числа N.
2. Складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления полученной суммы на 2.
3. Предыдущий пункт повторяется для записи с добавленной цифрой.
4. Результат переводится в десятичную систему и выводится на экран.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
1. Двоичная запись числа N: 1101.
2. Сумма цифр двоичной записи 3, остаток от деления на 2 равен 1, новая запись 11011.
3. Сумма цифр полученной записи 4, остаток от деления на 2 равен 0, новая запись 110110.
4. На экран выводится число 54.
Сколько различных чисел, принадлежащих отрезку [20; 50], могут появиться на экране в результате работы автомата?

Решение.
отрезок [20; 50]
Переведём 20 и 50 в Р=2
2010=101002; 5010= 1100102 красным обозначены добавленные биты,
т.е. 1012- это младшее число, которое по алгоритму даст число,
входящее в этот отрезок,
а 11002 - это старшее число, которое по алгоритму даст число,
входящее в этот отрезок.
В десятичной системе счисления это числа 5 и 12, т.е. 5 ≤ х ≤12
X=12-5+1=8
Ответ: 8 чисел

№1 Автомат обрабатывает натуральное число N по следующему алгоритму:
1. Строится двоичная запись числа N.
2. Складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления полученной суммы на 2.
3. Предыдущий пункт повторяется для записи с добавленной цифрой.
4. Результат переводится в десятичную систему и выводится на экран.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
1. Двоичная запись числа N: 1101.
2. Сумма цифр двоичной записи 3, остаток от деления на 2 равен 1, новая запись 11011.
3. Сумма цифр полученной записи 4, остаток от деления на 2 равен 0, новая запись 110110.
4. На экран выводится число 54.
Сколько различных чисел, принадлежащих отрезку [90; 160], могут появиться на экране в результате работы автомата?
Самостоятельно

№2. Автомат обрабатывает натуральное число N по следующему алгоритму:
1. Строится двоичная запись числа N.
2. Складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления полученной суммы на 2.
3. Предыдущий пункт повторяется для записи с добавленной цифрой.
4. Результат переводится в десятичную систему и выводится на экран.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
1. Двоичная запись числа N: 1101.
2. Сумма цифр двоичной записи 3, остаток от деления на 2 равен 1, новая запись 11011.
3. Сумма цифр полученной записи 4, остаток от деления на 2 равен 0, новая запись 110110.
4. На экран выводится число 54.
Сколько различных чисел, меньших 50, могут появиться на экране в результате работы автомата?

ОТВЕТЫ
№1- 19
№2 - 12

ДРУГИЕ ВАРИАНТЫ ЗАДАНИЯ

Автомат обрабатывает натуральное число N (0 ≤ N ≤ 255) по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3) Полученное число переводится в десятичную запись.
4) Из нового числа вычитается исходное, полученная разность выводится на экран.
Пример.
Дано число N = 13. Алгоритм работает следующим образом:
1) Восьмибитная двоичная запись числа N: 00001101.
2) Все цифры заменяются на противоположные, новая запись 11110010.
3) Десятичное значение полученного числа 242.
4) На экран выводится число 242 – 13 = 229.
Какое число нужно ввести в автомат, чтобы в результате получилось 113?

Решение.
Речь идет об однобайтовом представлении, которое применяется только для положительных целых чисел , т.е. в этом формате отсутствует знаковый разряд и
отрицательные числа.
Когда мы выполняем инверсию в 8 разрядах
(заменяем все 0 на 1 и наоборот), мы фактически вычитаем исходное число из числа 255.

Т.е. инверсия двоичной восьмибитной записи числа в сумме с исходным числом дает 11111111, то есть 255.
(В исходном примере(13+242=255) ⇒ 000011012 + 111100102 = 111111112.)
Следовательно, если исходное число равно N , то инвертированное число равно 255 − N. Затем автомат осуществляет вычитание, вычисляя 255 − 2N.
Поэтому, чтобы найти число, которое нужно ввести в автомат для получения 113,
нужно решить уравнение 255 − 2N = 113. ⇒ N=71.
Ответ: 71

Автомат обрабатывает натуральное число N по следующему алгоритму::
1) Строится двоичная запись числа N.
2) Запись «переворачивается», то есть читается справа налево. Если при этом появляются ведущие нули, они отбрасываются.
3) Полученное число переводится в десятичную запись и выводится на экран.
Какое наибольшее число, не превышающее 100, после обработки автоматом даёт результат 9?
Решение.
Переводим 9 и 100 в Р=2 ⇒ 9=10012; 100= 11001002
Число д.б. наибольшим, но меньше 11001002
Переворачиваем число 9 ⇒ 10012
Тогда исходное число должно начинаться на 10012 и далее пойдут нули, которые отброшены при перевороте числа, т.е. 100100002,
но 100100002=14410 > 100. Делим на 2, т.е. убираем один 0.
Это число 10010002=7210
Ответ : 72

Автомат обрабатывает натуральное число N по следующему алгоритму:
1) Строится двоичная запись числа N.
2) Из записи удаляются все нули.
3) Полученное число переводится в десятичную запись и выводится на экран.
Сколько разных значений будет показано на экране автомата при последовательном вводе всех натуральных чисел от 10 до 2500?

Ответ: 11
Решение: посмотрим, что происходит при удалении нулей. Возьмём число 10: 10102 => 11. Ясно, что после удаления нулей мы можем получать только числа, которые в двоичной записи содержат только единицы. Попробуем узнать, какое максимальное количество единиц мы можем получить.
2500 > 2048 = 211 . 211 выглядит как 1000000000002 (единица и 11 нулей), предыдущее число 2047 выглядит как 111111111112 (11 единиц).
12 единиц – это число 212-1 = 4096 – 1 = 4095, его получить мы не можем, т.е. 11 единиц наш максимум.
Если мы начнём с правого края заменять единицы на нули, то получим:
111111111112
111111111102
111111111002
...
100000000002
11 разных чисел. Эти же 11 чисел можно получить и из других исходных чисел (например, одну единицу можно получить из числа 100000000002
и из числа 100002), но в любом случае количество различных чисел, которые будут выведены в результате на экран, равно 11.

Автомат обрабатывает натуральное число N (0≤N≤255) по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Удаляется последняя цифра двоичной записи.
3) Запись «переворачивается», то есть читается справа налево.
4) Полученное число переводится в десятичную запись и выводится на экран.
Какое наибольшее число, меньшее 100, не изменится после обработки автоматом?

Ответ: 90
Решение: посмотрим, что происходит с числом во время работы автомата. Предположим, исходное число в двоичной системе счисления выглядело как
abcdefgh2
После удаления последней цифры оно превратилось в abcdefg2.
После переворота оно превратилось в gfedcba2. Если оно равно исходному,
то получаем:
abcdefgh2
0gfedcba2
Т.е. а соответствует 0. Тогда число выглядит как 0bcddcb02
Попробуем найти это число.
Если b = 1, то к числу нужно будет прибавить 64 + 2 = 66.
Если c = 1, то к числу нужно будет прибавить 32 + 4 = 36
Если d = 1, то к числу нужно будет прибавить 16 + 8 = 24.
Попробуем набрать максимальную сумму, которая меньше 100. Это 66 + 24 = 90, 010110102. Это и есть ответ.

Автомат обрабатывает натуральное число N по следующему алгоритму:
1. Строится двоичная запись числа N без ведущих нулей.
2. Если в полученной записи единиц больше, чем нулей, то справа приписывается единица. Если нулей больше или нулей и единиц поровну, справа приписывается ноль.
3. Полученное число переводится в десятичную запись и выводится на экран.
Какое наименьшее число, превышающее 36, может получиться в результате работы автомата?

Ответ: 39
Решение: подбором.
Возьмём число 36. В двоичной СС оно выглядит как 1001012. Это – результат работы алгоритма, т.е.
1001002, где 10010 – число, которое было подано на вход алгоритму, 0 – что дописал алгоритм. По условию нам нужно найти число, большее 36. Начнём перебирать числа:
1001012 (37) – не подходит, т.к. на конце должен стоять 0, не 1.
1001102 (38) – не подходит, т.к. на конце должна стоять 1, не 0.
1001112 (39) – подходит.

Автомат обрабатывает натуральное число N по следующему алгоритму.
1. Строится двоичная запись числа N.
2. Удаляются первая слева единица и все следующие непосредственно за
ней нули. Если после этого в числе не остаётся цифр, результат этого
действия считается равным нулю.
3. Полученное число переводится в десятичную запись.
4. Новое число вычитается из исходного, полученная разность выводится на экран.
Пример. Дано число N = 11. Алгоритм работает следующим образом.
1. Двоичная запись числа N: 1011.
2. Удаляется первая единица и следующий за ней ноль: 11.
3. Десятичное значение полученного числа 3.
4. На экран выводится число 11 – 3 = 8.
Сколько разных значений будет показано на экране автомата при последовательном вводе всех натуральных чисел от 500 до 5000?

Ответ: 5
Решение: посмотрим, что происходим с числом при работе автомата.
500 = 1111101002.
Удаляем ведущую 1 и считаем разность:
1111101002 - 0111101002 = 1000000002 (единица и 8 нулей)
Понятно, что в результате работы алгоритма мы всегда будем получать единицу и далее нули. 1000000002 число, которое можно получить, максимальное получается после обработки числа 5000:
10011100010002 -> 10000000000002 (единица и 12 нулей).
Все числа:
единица и 8 нулей, единица и 9 нулей, единица и 10 нулей, единица и 11 нулей, единица и 12 нулей.
Всего 5 различных чисел.

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3) Полученное число переводится в десятичную запись.
4) Из нового числа вычитается исходное, полученная разность выводится на экран.
Какое число нужно ввести в автомат, чтобы в результате получилось 45?
Самостоятельно

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3) Полученное число переводится в десятичную запись.
4) Из нового числа вычитается исходное, полученная разность выводится на экран.
Какое число нужно ввести в автомат, чтобы в результате получилось «–21»?

Автомат обрабатывает натуральное число N по следующему алгоритму:
1) Строится двоичная запись числа N.
2) Запись «переворачивается», то есть читается справа налево. Если при этом появляются ведущие нули, они отбрасываются.
3) Полученное число переводится в десятичную запись и выводится на экран.
Какое наибольшее число, не превышающее 500, после обработки автоматом даёт результат 13?

4) Автомат обрабатывает натуральное число N по следующему алгоритму:
1) Строится двоичная запись числа N.
2) Запись «переворачивается», то есть читается справа налево. Если при этом появляются ведущие нули, они отбрасываются.
3) Полученное число переводится в десятичную запись и выводится на экран.
Какое наибольшее число, не превышающее 500, после обработки автоматом даёт результат 13?

5) Автомат обрабатывает натуральное число N (0≤N≤255) по следующему алгоритму:
1) Строится восьми битная двоичная запись числа N.
2) Удаляются средние 4 цифры.
3) Полученное число переводится в десятичную запись и выводится на экран.
Какое наименьшее число, большее 130, после обработки автоматом даёт результат 10?

6) Автомат обрабатывает натуральное число N (0≤N≤255) по следующему алгоритму:
1) Строится восьми битная двоичная запись числа N.
2) Удаляются средние 4 цифры.
3) Полученное число переводится в десятичную запись и выводится на экран.
Какое наибольшее число, меньшее 110, после обработки автоматом даёт результат 7?

7) Автомат обрабатывает натуральное число N < 256 по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Инвертируются все разряды исходного числа, кроме последней единицы и стоящих за ней нулей (0 заменяется на 1, 1 на 0).
3) Полученное число переводится в десятичную систему счисления.
Чему равен результат работы алгоритма для N = 211?

8) Автомат обрабатывает натуральное число N по следующему алгоритму:
1) Строится двоичная запись числа N.
2) Удаляются две последние цифры.
3) Полученное число переводится в десятичную запись и выводится на экран.
Сколько разных значений будет показано на экране автомата при последовательном вводе всех натуральных чисел от 20 до 600?

ОТВЕТЫ
№1- 105
№2 - 138
№3 - 352
№4 - 112
№5 - 134
№6 – 107
№7 – 45
№8 – 146

№1. Автомат обрабатывает трёхзначное натуральное число N по следующему алгоритму.
1. Из цифр, образующих десятичную запись N, строятся наибольшее и наименьшее возможные двузначные числа (числа не могут начинаться с нуля).
2. На экран выводится разность полученных двузначных чисел.
Пример. Дано число N = 351. Алгоритм работает следующим образом.
Наибольшее двузначное число из заданных цифр – 53,
наименьшее – 13.
2. На экран выводится разность 53 – 13 = 40.
Чему равно количество чисел N на отрезке [100; 200], в результате обработки которых на экране автомата появится число 30?

Решение:
Пусть исходное число записывалось как abc (a*100 + b*10 + c). Предположим, что a >= b >= c. Тогда наибольшее двузначное число, которое можно составить, выглядит как ab (a*10 + b), а вот наименьшее – либо cb (если c <> 0), либо b0 (если c = 0), либо a0 (если и b, и c равны 0). Т.к. разность равна 30, наименьшее число выглядит как cb.
(a*10 + b) - (c*10 + b) = 30
a - c = 3

Возможные варианты:
a = 9, c = 6 (6 <= b <= 9, 4 варианта)
a = 8, c = 5 (5 <= b <= 8)
a = 7, c = 4 (4 <= b <= 7)
a = 6, c = 3 (3 <= b <= 6)
a = 5, c = 2 (2 <= b <= 5)
a = 4, c = 1 (1 <= b <= 4)
a = 3, c = 0 - вариант невозможен, т.к. в таком случае cb - не двузначное число
В исходном числе a, b и c могут стоять в любом порядке.
Т.к. исходное число должно принадлежать отрезку [100; 200], подходит только последний вариант: a = 4, c = 1 (1 <= b <= 4). Первой цифрой будет 1 (т.е. с), a и b могут меняться местами. Всего 4 варианта, когда а стоит на втором месте (14*), и 4 варианта, когда а стоит на 3-м месте (1*4), но число 144 повторяется дважды, поэтому на самом деле общее количество вариантов не 4+4=8, а 7.
Ответ: 7

Самостоятельно
№1. Автомат обрабатывает трёхзначное натуральное число N по следующему алгоритму.
1. Из цифр, образующих десятичную запись N, строятся наибольшее и наименьшее возможные двузначные числа (числа не могут начинаться с нуля).
2. На экран выводится разность полученных двузначных чисел.
Пример. Дано число N = 351. Алгоритм работает следующим образом.
1. Наибольшее двузначное число из заданных цифр – 53, наименьшее – 13.
2. На экран выводится разность 53 – 13 = 40.
Чему равно количество трёхзначных чисел N, в результате обработки которых на экране автомата появится число 35?

Ответ: 4
Решение: сперва рассмотрим только числа abc, a>= b >= c. Остальные числа получим перестановкой a, b, c.
Наибольшее число будет равно ab, а вот наименьшее – либо cb (если
c <> 0), либо b0 (если c = 0), либо a0 (если и b, и c равны 0).
Разность равна 35, единственный вариант, который подходит – это bc.
(a*10 + b) – (b*10 + 0) = 35
(a-b)*10 + b = 35
b = 5, a = 8, c = 0
0 в начале числа стоять не может, поэтому получаем только следующие комбинации:
850, 805, 580, 508
Всего 4 числа.

Самостоятельно
Автомат обрабатывает трёхзначное натуральное число N по следующему алгоритму.
1. Из цифр, образующих десятичную запись N, строятся наибольшее и наименьшее возможные двузначные числа (числа не могут начинаться с нуля).
2. На экран выводится разность полученных двузначных чисел.
Пример. Дано число N = 351. Алгоритм работает следующим образом.
1. Наибольшее двузначное число из заданных цифр – 53, наименьшее – 13.
2. На экран выводится разность 53 – 13 = 40.
Чему равно наибольшее возможное трёхзначное число N, в результате обработки которого на экране автомата появится число 50?