содержательный подход

Содержание
Количество информации как мера уменьшения неопределенности знаний
Определение количества информации

Информативность сообщения
Если сведения «старые», то есть человек это уже знает, или содержание сообщения непонятно человеку, то для него это сообщение неинформативно.
Информативно то сообщение, которое содержит новые и понятные сведения.

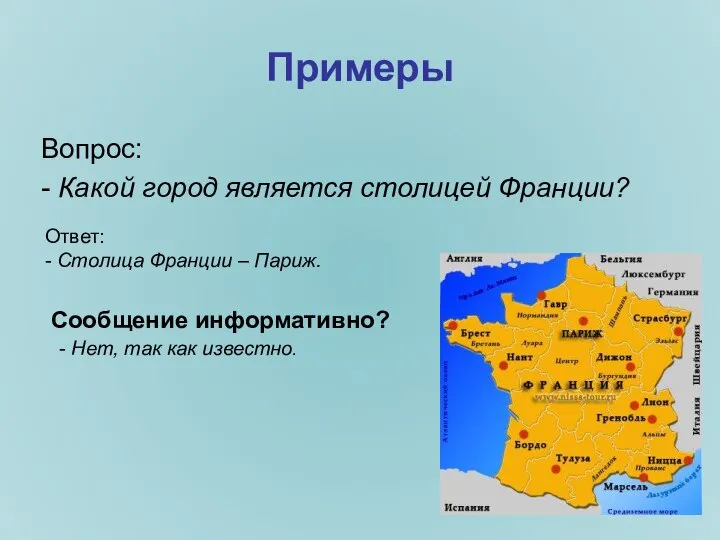
Примеры
Вопрос:
- Какой город является столицей Франции?
Ответ:
- Столица Франции – Париж.
Сообщение информативно?
- Нет, так как известно.

Примеры
Вопрос:
- Что изучает коллоидная химия?
Ответ:
- Коллоидная химия изучает дисперсионные состояния систем, обладающих высокой степенью раздробленности.
Сообщение информативно?
- Нет, так не понятно.

Примеры
Вопрос:
- Какую высоту и вес имеет Эйфелева башня?
Ответ:
- Эйфелева башня имеет
высоту 300 метров
и вес 9000 тонн.
Сообщение информативно?
- Да.

Информативность сообщения
Если сообщение неинформативно для человека, то количество информации в нем с точки зрения этого человека равно нулю.
Количество информации в информативном сообщении больше нуля.

Информация и неопределенность
Пример: вы услышали по телевизору, что завтра будет солнечная погода.
Ваше состояние изменилось: вы стали обладателем информации, а неопределенность, которая до этого существовала, исчезла.

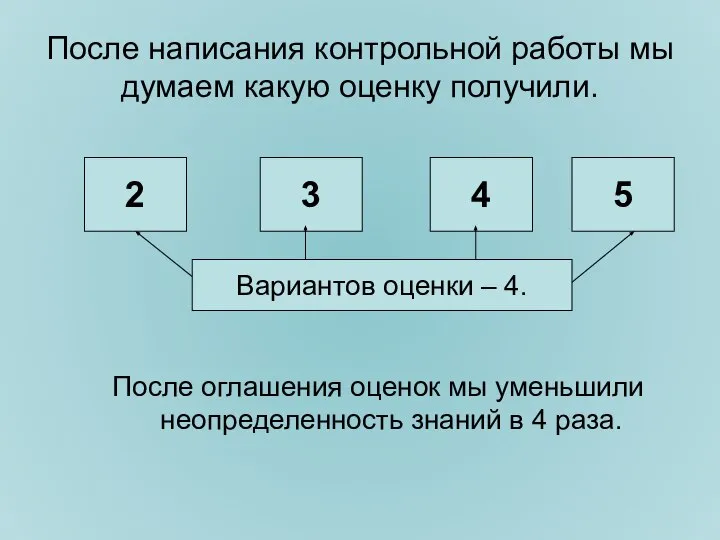
После написания контрольной работы мы думаем какую оценку получили.
После оглашения оценок мы уменьшили неопределенность знаний в 4 раза.

Бросание монет
У монеты, как известно, две стороны:
«герб» «решка»
Если бросить ее на стол, монета обязательно упадет вверх либо «гербом», либо «решкой».
Таким образом, монету, лежащую на столе, можно рассматривать как простейшую систему, которая может находиться в одном из двух возможных состояний.

Бросание кубика
Игральный кубик — это кубик, грани которого пронумерованы от 1 до 6.
Аналогично монете игральный кубик, лежащий на столе, — это система, находящаяся в одном из шести возможных состояний (по номерам граней, обращенных вверх).

Неопределенность знаний
Неопределенность знания о результате некоторого события – это число возможных вариантов результата.
Для монеты – 2, для кубика – 6, для билетов – 30 (если на столе лежало 30 билетов).
Чем больше равновозможных событий, тем больше неопределенность ситуации.

Равновероятные события
События равновероятны, если ни одно из них не имеет преимущества перед другими.
С этой точки зрения выпадение «герба» или «решки» – равновероятно.

Определение количества информации

Как же измерить количество информации?
Да также, как мы измеряем длину или массу чего-нибудь: сравнить с соответствующим эталоном.
Надо только выбрать эталон.
Например, в мультфильме
«38 попугаев» эталоном длины
служит длина шага попугая.
Каков же эталон для измерения информации?
Давайте в этом разберемся.

1 бит информации
Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.
Сообщение, уменьшающее неопределенность знаний в 2 раза, несет 1 бит информации.
Сообщение о том, что произошло одно событие из двух равновероятных, несет 1 бит информации.
Бит - binary digit (двоичный знак).

Определение информации
Если «Ваньку-Встаньку» качнуть, то сколько различных вариантов его конечного состояния получим?
- Один вариант («Ванька-Встанька» всегда встает).
То есть вероятность события равна 1 (100% выполнение).
И мы не получаем ни чего нового и неизвестного при этом, то есть информация равна 0.

Определение информации
Будем бросать монету.
Сколько вариантов выпадения может быть? – 2
Вероятность выпадения «герба» или «решки» - ½.
Количество информации – 1 бит.

Определение информации
Будем бросать 2 монеты.
Бросание 2 монет должно
принести 2 бита информации, так как количество монет увеличилось в 2 раза.
Количество различных вариантов выпадения по две монеты: 4.
Вероятность появления 1 варианта – ¼

Определение информации
Будем бросать 3 монеты.
При бросание 3 монет количество информации увеличится в 3 раза по сравнению с бросанием 1 монеты.
Количество различных вариантов выпадения по 3 монеты: 8
Вероятность выпадения 1 варианта: 1/8.

Отгадывание чисел
Допустим кто-то загадал число от 1 до 16.
Сколько чисел можно загадать? - 16.
Вероятность загадать любого числа из этого промежутка: 1/16.
Отгадывание происходит по такому сценарию:
Задается такой вопрос на который можно получить один из вариантов ответа: «да» или «нет».

Сценарий отгадывания числа
Пусть загадано число 5 (мы не знаем это).
1 вопрос (даст 1 бит информации):
- Больше 8? – Нет.
2 вопрос (даст 2 бит информации):
- Больше 4? – Да.
3 вопрос (даст 3 бит информации):
-Больше 6? – Нет.
4 вопрос (даст 4 бит информации):
-Больше 5? – Нет.
Ответ: Задуманное число 5.
Вывод:
При отгадывании задуманного числа в диапазоне от 1 до 16, достаточно 4 вопроса (получение 4 бита информации).

Определение информации
А если мы будем бросать 6-гранный кубик?
Количество вариантов выпадения одной из 6 сторон: 6.
Вероятность выпадения одной из 6 сторон: 1/6.
Сколько же будет получено
информации при выпадении
одной из 6 сторон?

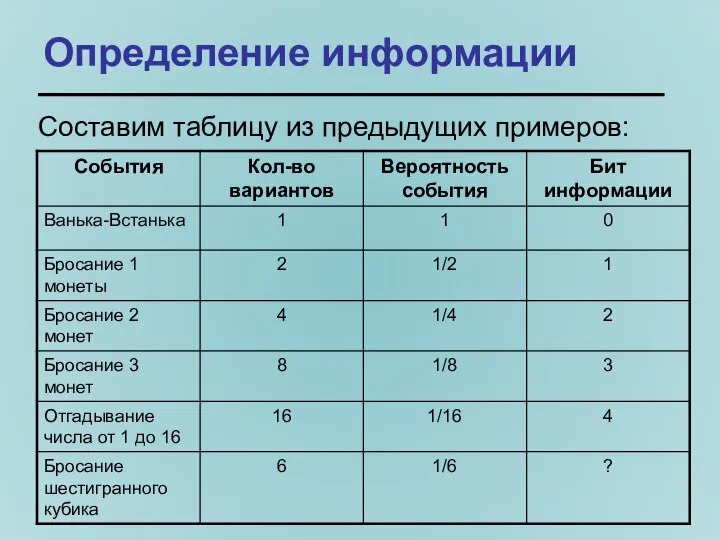
Определение информации
Составим таблицу из предыдущих примеров:

Определение информации
Если посмотреть таблицу, то можно заметить закономерность.
От частных примеров приходим к обобщенной формуле:
Если ввести обозначения:
N – число вариантов равновероятных событий (неопределенность знаний),
i – количество информации в сообщении о том, что произошло одно из N событий.
N = 2i

Определение информации
Если N = 2 (2=21),
то уравнение примет вид 2i = 21,
отсюда i = 1.
Если N = 4 (4=22),
то уравнение примет вид 2i = 22,
отсюда i = 2.
Если N = 8 (8=23),
то уравнение примет вид 2i = 23,
отсюда i = 3.
В общем случае, если N = 2k,
где k- целое число,
то уравнение примет вид 2i = 2k,
отсюда i = k.

Определение информации
Например, желая определить, сколько же бит информации несет сообщение о результате бросания шестигранного кубика, нужно решить уравнение
2i = 6.
Поскольку 22 < 6 < 23, то получаем 2 < i < 3.
Используя инженерный калькулятор, узнаем, что i=2,58496.

Задания для закрепления
Пример 1.
Сколько информации несет сообщение о том, что из колоды карт достали карту красной масти?
Решение:
1 бит, т. к. N = 2 (красных и черных карт одинаковое количество).
2i = 2

Задания для закрепления
Пример 2.
Сколько информации несет сообщение о том, что из колоды карт достали карту бубновой масти?
Решение:
2 бита, так как т. к. N = 4 (всего в колоде 4 масти, и количество карт в них одинаковое).
2i = 4

Задания для закрепления
Пример 3.
Проводятся две лотереи «4 из 32» и «5 из 64».
Сообщение о результатах, какой из лотерей
несет больше информации?

Решение:
Вытаскивание любого номера из лотерейного барабана – события равновероятные.
Поэтому в первой лотерее количество информации в сообщении об одном номере равно 5 бит (25 = 32), а во втором – 6 бит (26 = 64).
Сообщение о 4-х номерах в первой лотерее несет 5 * 4 = 20 бит.
Сообщение о 5-ти номерах второй лотереи несет 6 * 5 = 30 бит.
Следовательно, сообщение о результатах второй лотереи несет больше информации, чем первой.

Задания для закрепления
Пример 4.
В течение четверти ученик получил 100 оценок.
Сообщение о том, что он получил четверку, несет 2 бита информации.
Сколько четверок ученик получил за четверть?

Решение:
Данный результат мог быть получен путем следующих рассуждений:
2 бита информации несет сообщение об одном из четырех равновероятных событий (22 = 4).
То есть вероятность получения четверок равна ¼.
Тогда количество четверок определится как:
100 / 4 = 25.
Таким образом, в течение четверти ученик получил 25 четверок.

Единицы измерения
количества информации
1 байт = 8 битов = 23 битов
1 килобайт (Кбайт) = 210 байт = 1024 байт
1 мегабайт (Мбайт) = 210 Кбайт = 1024 Кбайт
1 гигабайт (Гбайт) = 210 Мбайт = 1024 Мбайт
1 терабайт (Тбайт) = 210 Гбайт = 1024 Гбайт

Самостоятельное решение
Задача 1.
Вы подошли к светофору, когда горел желтый свет.
После этого загорелся зеленый.
Какое количество информации вы при этом получили?
Ответ: 1бит

Самостоятельное решение
Задача 2.
Сообщение о том, что ваш друг живет на 9 этаже, несет 4 бита информации. Сколько этажей в доме?
Ответ: 16 (24 = 16).

Самостоятельное решение
Задача 3.
В корзине 8 шаров.
Все шары разного цвета.
Сколько информации несет сообщение о том, что из корзины достали красный шар?
Ответ: 3 бит (23 = 8).

Самостоятельное решение
Задача 4.
Сколько бит информации несет сообщение о том, что из колоды в 32 карты достали даму крести?
Ответ: 5 бит (2X = 32).

Самостоятельное решение
Задача 5.
в школьной библиотеке 16 стеллажей с книгами.
На каждом стеллаже 8 полок.
Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке.
Какое количество информации библиотекарь передал Пете?
Ответ: 7 бит
16*8 = 128 полок всего
2Х = 128

Самостоятельное решение
Задача 6.
При угадывании целого числа в некотором диапазоне было получено 6 бит информации.
Сколько чисел содержится в этом диапазоне?
Ответ: 64 (26 = 64).

Самостоятельное решение
Задача 7.
Сообщение о том, что Петя живет во втором подъезде, несет 3 бита информации.
Сколько подъездов в доме?
Ответ: 8 (23 = 8).

Разновероятностный подход
В 1948 г. американский инженер и математик К Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями.
Если i - количество информации,
k - количество возможных событий,
рi - вероятности отдельных событий,
то количество информации для событий с различными вероятностями можно определить по формуле:
i = - ∑ рi log2 рi,
где i принимает значения от 1 до k.

Задания для закрепления
Задача:
В коробке имеется 40 белых и 10 черных шаров. Определите количество информации.
Решение:
Всего шаров: 40+10 = 50
Вероятность вытащить белый шар:
рб =0,8
i = - ∑ рi log2 рi =-(рб * log2 рб + рч * log2 рч)
i =-(0,8 * log2 0,8 + 0,2 * log2 0,2) =….
Вероятность вытащить черный шар: рч =0,2

Самостоятельное решение
В пруду живут 8000 карасей, 2000 щук и 400000 пескарей.
Вероятнее наловить больше карасей, щук или пескарей.

Используемая литература
И. Семакин. Информатика. Базовый курс. 7 – 9 классы. – М.: Лаборатория Базовых Знаний, 2001. – 364 с.: ил.
Информатика. Задачник-практикум в 2 т./Под ред. И.Г. Семакина, Е.К. Хеннера: Том 1. – М.: Лаборатория Базовых Знаний, 2001. – 304 с.: ил.
Урок: Определение количества информации 8 класс: http://netedu.ru/node/3986
Решение задач на определение количества информации: http://uprobr.ucoz.ru/publ/informatika_i_ikt/reshenie_zadach_na_opredelenie_kolichestva_informacii/6-1-0-551
Карта Франции: http://tgekb.ru/pics500/userimages/article/frantsiya880090938francemap1.jpg
Коллоидная химия: http://www.char.ru/books/2066990_Kolloidnaya_himiya_Uchebnik_dlya_vuzov.jpg
Эйфелева башня: http://mosaica.ru/sites/default/files/news/preview/2010/02/27/888888888888888.jpg