9-1-4 (2)

Ключевые слова
таблица
таблица «объект – свойство»
таблица «объект – объект»

Представление информации
в табличной форме
Представленная в таблице информация наглядна, компактна и легко обозрима.
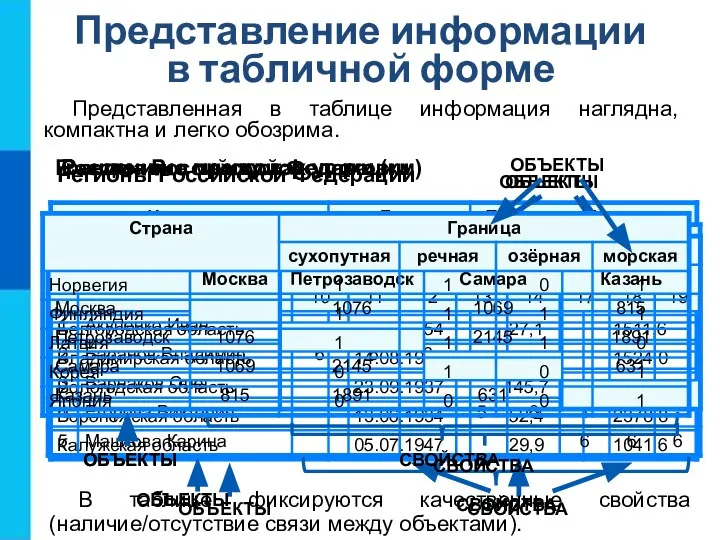
Регионы Российской Федерации
ОБЪЕКТЫ
СВОЙСТВА
Сведения о пропусках уроков
ОБЪЕКТЫ
СВОЙСТВА
ОБЪЕКТЫ
Расстояние между городами (км)
ОБЪЕКТЫ
СВОЙСТВА
ОБЪЕКТЫ
Граница Российской Федерации
В таблице фиксируются качественные свойства (наличие/отсутствие связи между объектами).
ОБЪЕКТЫ
СВОЙСТВА
ОБЪЕКТЫ

Задача о перекладывании камней
Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 3 камня, а во второй - 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16.
Кто выигрывает при безошибочной игре - игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока?
Ответ обоснуйте.

Задача о перекладывании камней
1-й ход: 1-й игрок увеличивает в три раза число камней в первой куче.
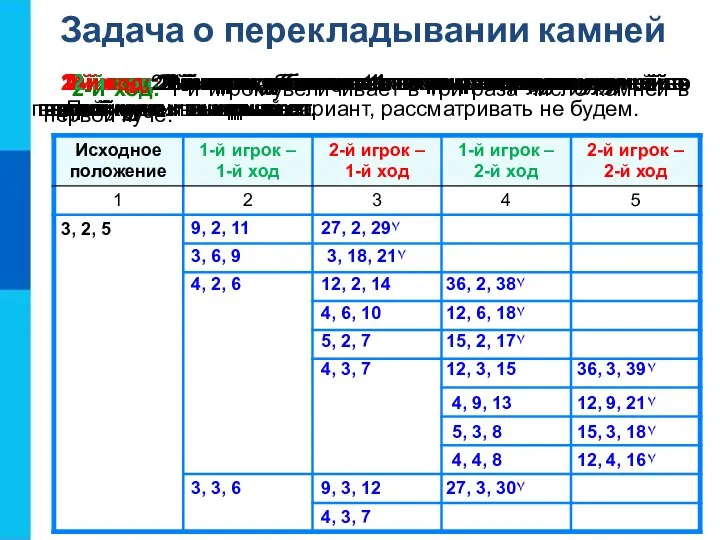
9, 2, 11
27, 2, 29٧
3, 6, 9
12, 4, 16٧
3, 18, 21٧
4, 4, 8
4, 2, 6
12, 2, 14
4, 6, 10
5, 2, 7
4, 3, 7
3, 3, 6
9, 3, 12
4, 3, 7
12, 3, 15
4, 9, 13
5, 3, 8
27, 3, 30٧
36, 2, 38٧
12, 6, 18٧
15, 2, 17٧
36, 3, 39٧
12, 9, 21٧
15, 3, 18٧
1-й ход: 2-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
1-й ход: 1-й игрок увеличивает в три раза число камней во второй куче.
1-й ход: 2-й игрок увеличивает в три раза число камней во второй куче и выигрывает.
1-й ход: 1-й игрок добавляет 1 камень в первую кучу.
1-й ход: 2-й игрок увеличивает в три раза число камней в первой куче.
2-й ход: 1-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
1-й ход: 2-й игрок увеличивает в три раза число камней во второй куче.
2-й ход: 1-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
1-й ход: 2-й игрок добавляет 1 камень в первую кучу.
2-й ход: 1-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
1-й ход: 2-й игрок добавляет 1 камень во вторую кучу.
2-й ход: 1-й игрок увеличивает в три раза число камней в первой куче.
2-й ход: 2-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
2-й ход: 1-й игрок увеличивает в три раза число камней во второй куче.
2-й ход: 2-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
2-й ход: 1-й игрок добавляет 1 камень в первую кучу.
2-й ход: 2-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
2-й ход: 1-й игрок добавляет 1 камень во вторую кучу.
2-й ход: 2-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
1-й ход: 1-й игрок добавляет 1 камень во вторую кучу.
1-й ход: 2-й игрок увеличивает в три раза число камней в первой куче.
2-й ход: 1-й игрок увеличивает в три раза число камней в первой куче и выигрывает.
1-й ход: 2-й игрок добавляет 1 камень в первую кучу.
Получили повторный вариант, рассматривать не будем.

Таблицы и графы
Таблица «Схема дорог»
Взвешенный граф
Если между парой населённых пунктов существует дорога, то в ячейку на пересечении соответствующих строки и столбца записывается число, равное её длине. Пустые клетки в таблице означают, что дорог между соответствующими населёнными пунктами нет.
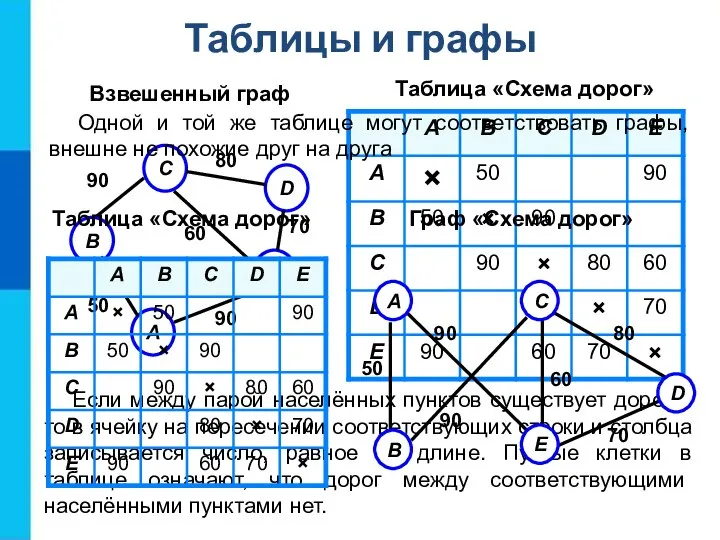
Граф «Схема дорог»
Одной и той же таблице могут соответствовать графы, внешне не похожие друг на друга
Таблица «Схема дорог»

Задача о коктейлях
Три подружки - Аня, Света и Настя - купили различные молочные коктейли в белом, голубом и зелёном стаканчиках. Ане достался не белый стаканчик, а Свете - не голубой. В белом стаканчике не банановый коктейль. В голубой стаканчик налит ванильный коктейль. Света не любит клубничный коктейль.
Требуется выяснить, какой коктейль и в каком стаканчике купила каждая из девочек.

Задача о коктейлях
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
Ответ: Аня купила ванильный коктейль в голубом стаканчике, Света - банановый коктейль в зелёном стаканчике, Настя - клубничный коктейль в белом стаканчике.
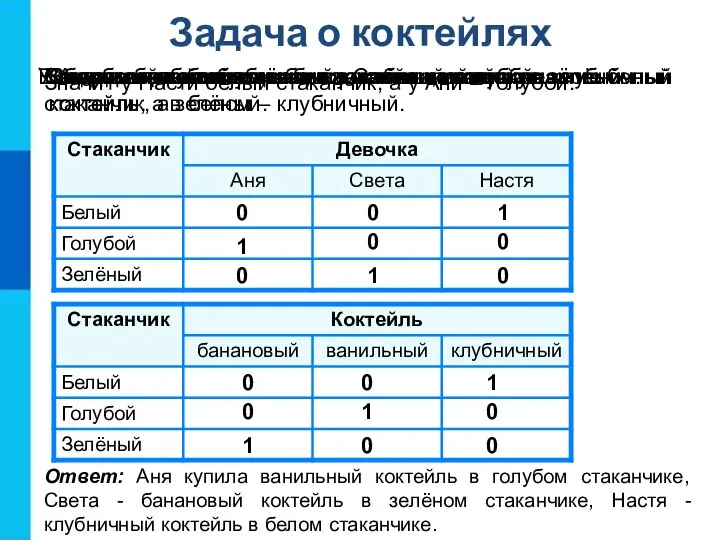
У Ани не белый стаканчик, а у Светы не голубой.
Создадим две таблицы:
В белом стаканчике не банановый коктейль.
В голубом стаканчике налит ванильный коктейль.
Значит в голубом стаканчике не банановый и не клубничный коктейль.
Ванильный коктейль не белом стаканчике и не в зелёном.
Следовательно в зелёном стаканчике налит банановый коктейль, а в белом – клубничный.
Света не любит клубничный коктейль, значит у неё не белый стаканчик, а зелёный.
Значит у Насти белый стаканчик, а у Ани – голубой.

Самое главное
Представленная в таблице информация наглядна, компактна и легко обозрима.
Таблица типа «объект - свойство» - это таблица, содержащая информацию о свойствах отдельных объектах, принадлежащих одному классу.
Таблица типа «объект - объект» - это таблица, содержащая информацию о некотором одном свойстве пар объектов, чаще всего принадлежащих разным классам.

Вопросы и задания
Какие преимущества обеспечивают табличные информационные модели по сравнению со словесными описаниями? Приведите пример.
Приведите примеры табличных информационных моделей, с которыми вы имеете дело:
а) на уроках в школе;
б) в повседневной жизни.
К какому типу относится таблица «Табель успеваемости», расположенная в конце вашего дневника?
Узнайте, в каких случаях в ячейку таблицы ставится знак «×».
Почему мы использовали этот знак в таблице?
Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 1 камень, а во второй - 2 камня.
У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 17.
Кто выигрывает при безошибочной игре обоих игроков - игрок, делающий первый ход, или игрок, делающий второй ход?
Каким должен быть первый ход выигрывающего игрока?
Ответ обоснуйте.
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями.
Если пересечение строки и столбца пусто, то станции не являются соседними. Стоимость проезда по маршруту складывается из стоимостей проезда между соседними станциями. Перевозки между населёнными пунктами A, B, C, D, F осуществляют три компании,представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость проезда из А в B?
1)
2)
3)
Соревнования по плаванию были в самом разгаре, когда стало ясно, что первые четыре места займут мальчики из пятёрки лидеров. Их имена: Валерий, Николай, Михаил, Игорь, Эдуард, фамилии: Симаков, Чигрин, Зимин, Копылов, Блинов (имена и фамилии названы в произвольном порядке).
Нашлись знатоки, которые предсказали, что первое место займёт Копылов, второе - Валерий, третье - Чигрин, четвёртое - Эдуард.
Но ни один из ребят не занял того места, какое ему предсказывали.
На самом деле первое место завоевал Михаил, второе - Симаков, третье - Николай, четвёртое - Блинов, а Чигрин не попал в четвёрку сильнейших.
Назовите имя и фамилию каждого из лидеров.
В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары (в каждом городе - одна пара).
Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина.
Антон живёт в Норильске, Борис и Ольга - супруги, Григорий и Светлана не живут в одном городе, Мария живёт в Москве, Светлана - в Ростове.
В каком городе проживает каждая из супружеских пар?
Постройте граф, отражающий разновидности информационных моделей.