Содержание
- 2. Разработана Arne Andersson, Igal Galperin, Ronald L. Rivest в 1962г. Ronald L. Rivest Arne Andersson
- 3. Определение
- 4. Понятия, необходимые для работы с данным деревом: ?−дерево ????[?]−корень дерева ? ????[?],???ℎ?[?]−левые и правый "сын" вершины
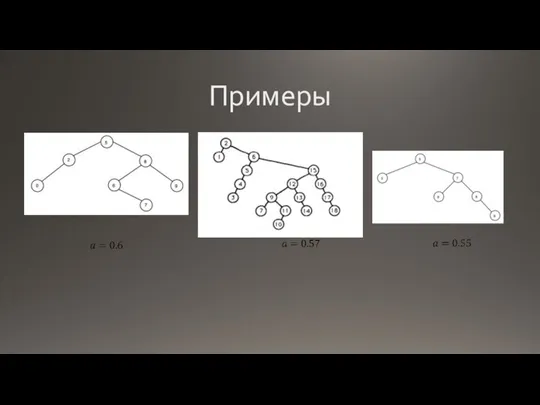
- 6. Примеры
- 7. Плюсы и минусы Scapegoat дерева Плюсы Скорость одних операций возможно улучшить за счет других операций. Scapegoat
- 8. Минусы В худшем случае операции модификации дерева могут занять ?(?) времени. В случае неправильного выбора парметра
- 9. Поиск
- 10. Вставка Начинается вставка нового элемента в Scapegoat-дерево классически: поиском ищем место, куда бы подвесить новую вершину
- 11. Перебалансировка Обходим всё поддерево Scapegoat-вершины (включая её саму) с помощью in-order обхода — на выходе получаем
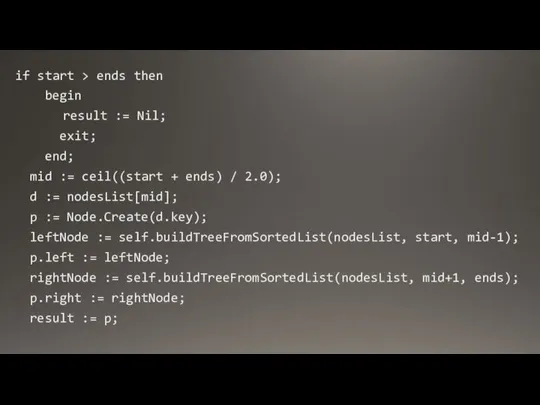
- 12. if start > ends then begin result := Nil; exit; end; mid := ceil((start + ends)
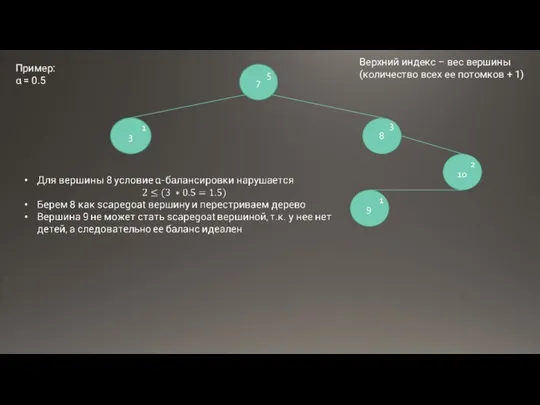
- 13. 7 3 8 1 10 2 9 1 3 5 Пример: α = 0.5 Верхний индекс
- 14. 8 1 Вычислив медиану (2) (start = 0, ends = 4), подвешиваем 8 в качестве корня
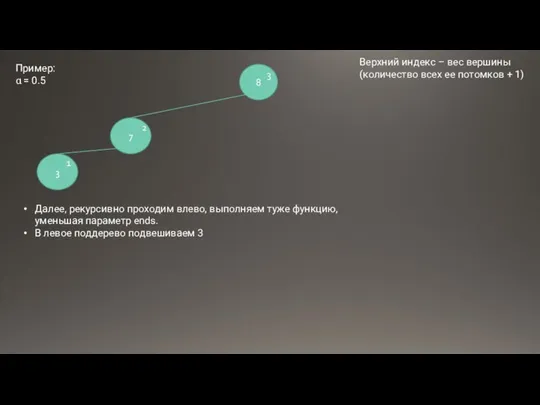
- 15. 8 7 1 2 Далее, рекурсивно проходим влево, выполняем туже функцию, уменьшая параметр ends. В левое
- 16. 8 7 2 3 Далее, рекурсивно проходим влево, выполняем туже функцию, уменьшая параметр ends. В левое
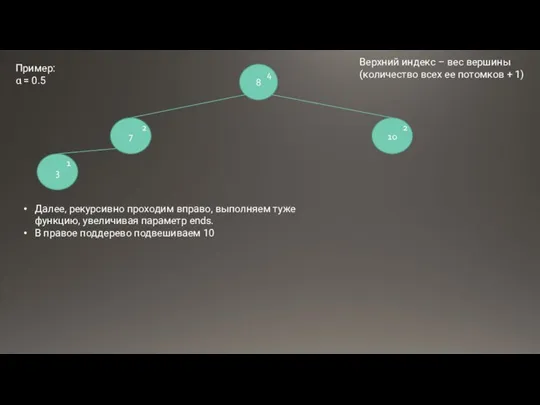
- 17. 8 7 2 4 Далее, рекурсивно проходим вправо, выполняем туже функцию, увеличивая параметр ends. В правое
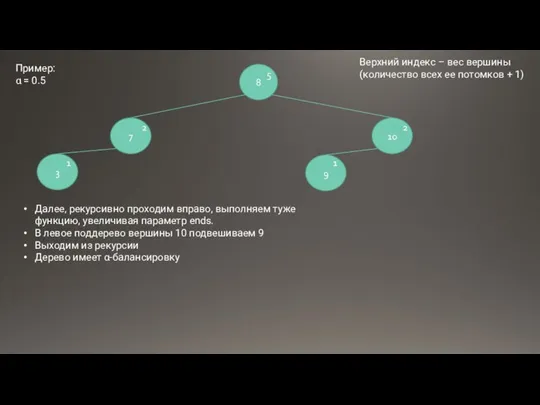
- 18. 8 7 2 5 Далее, рекурсивно проходим вправо, выполняем туже функцию, увеличивая параметр ends. В левое
- 20. Скачать презентацию


![Понятия, необходимые для работы с данным деревом: ?−дерево ????[?]−корень дерева ? ????[?],???ℎ?[?]−левые](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1172784/slide-3.jpg)








 Приложение для сортировки аудиофайлов
Приложение для сортировки аудиофайлов Инструкция по пользованию moodle
Инструкция по пользованию moodle Приложения, использующие децентрализованную систему
Приложения, использующие децентрализованную систему Как зарегистрироваться на конкурс
Как зарегистрироваться на конкурс Frontend. Основные теги
Frontend. Основные теги Современные веб-технологии. Лекция 2.1
Современные веб-технологии. Лекция 2.1 Построение биоритма человека в среде электронного процессора
Построение биоритма человека в среде электронного процессора Аддитивные технологии
Аддитивные технологии Модель OSI
Модель OSI Табличные информационные модели
Табличные информационные модели Информатика и компьютерная графика
Информатика и компьютерная графика Интерактивная система помощи иностранным студентам
Интерактивная система помощи иностранным студентам Книжный блог в INSTAGRAM как средство воспитания современного читателя
Книжный блог в INSTAGRAM как средство воспитания современного читателя Программирование (C++)
Программирование (C++) Форматы команд процессора. (Лекция 19.2)
Форматы команд процессора. (Лекция 19.2) Уменьшение файлов в размере
Уменьшение файлов в размере Добавлення інформації
Добавлення інформації Эскизное проектирование автоматизированной подсистемы отдела учета запчастей
Эскизное проектирование автоматизированной подсистемы отдела учета запчастей Создание веб-страниц в Word
Создание веб-страниц в Word Программирование на языке Си#. Форма
Программирование на языке Си#. Форма Дизайн пони
Дизайн пони Социальный проект Мотивация к обучению информатике группы 71-16 в последнюю неделю перед практикой
Социальный проект Мотивация к обучению информатике группы 71-16 в последнюю неделю перед практикой Будни Интернета: война ботов
Будни Интернета: война ботов Концепт непрерывного мира в игровой разработке
Концепт непрерывного мира в игровой разработке Криптография и шифрование
Криптография и шифрование Учебно-ознакомительная практика в пресс-службе ПГНИУ
Учебно-ознакомительная практика в пресс-службе ПГНИУ Чем и как полезен интернет?
Чем и как полезен интернет? Знакомство с Векторным редактором, встроеннЫм в WORD 2007
Знакомство с Векторным редактором, встроеннЫм в WORD 2007