Структура информации. Деревья. Графы

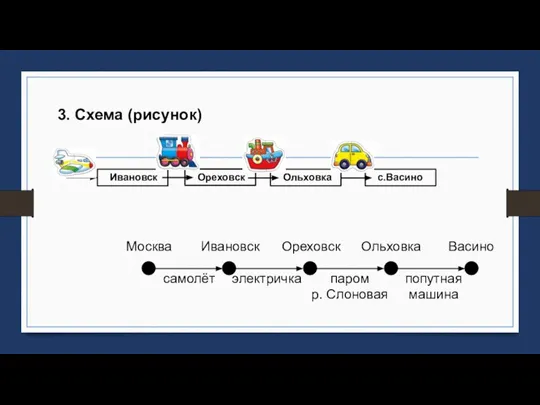
Структура информации
Для того чтобы добраться из Москвы до села Васино, нужно сначала долететь на самолете до города Ивановска. Затем на электричке доехать до Ореховска. Там на пароме переправиться через реку Слоновую в поселок Ольховка, и оттуда ехать в село Васино на попутной машине.
Зачем структурировать информацию?

1. Линейный список
Как доехать до села Васино:
На самолете из Москвы до г. Ивановска.
На электричке из г. Ивановска до г. Ореховска.
На пароме через реку Слоновую в пос. Ольховка.
На попутной машине из пос. Ольховка до с. Васино.
2. Таблица

3. Схема (рисунок)

Структурирование — это выделение важных элементов в информационных сообщениях и установление связей между ними.
Цель — облегчение восприятия и поиска информации.

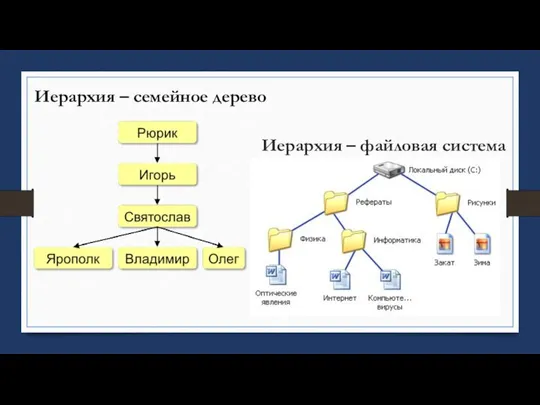
Структуры данных.
Иерархия (дерево) - одни элементы подчиняются другим

Иерархия – файловая система
Иерархия – семейное дерево

Что такое дерево?
Дерево (tree) — это структура, отражающая иерархию (отношения подчинённости, многоуровневые связи).

Дерево состоит из узлов и связей между ними (они называются дугами).
Самый первый узел, расположенный на верхнем уровне – это корень дерева. Конечные узлы, из которых не выходит ни одна дуга, называются листьями. Все остальные узлы, кроме корня и листьев, – это промежуточные узлы.
узел
дуга

Из двух связанных узлов тот, который находится на более высоком уровне, называется родителем, а другой – сыном.
Корень – это единственный узел, у которого нет родителя; у листьев нет сыновей.
Используются также понятия «предок» и «потомок».
Потомок какого-то узла – это узел, в который можно перейти по стрелкам от узла-предка
Соответственно, предок (parent) какого-то узла – это узел, из которого можно перейти по стрелкам в данный узел.

«Сыновья» А: B, C.
«Родитель» B: A.
«Потомки» А: B, C, D, E, F, G.
«Предки» F: A, C.
Корень (root) – узел, не имеющий предков (A).
Лист – узел, не имеющий потомков (D, E, F, G).
Высота дерева – это наибольшее расстояние (количество дуг) от корня до листа.
Высота дерева, приведённого на рисунке равна 2.

Дерево – это такая структура данных, которая представляет собой древовидную структуру в виде набора связанных узлов.
Чаще всего в информатике используются бинарные (двоичные) деревья, т. е. такие, в которых каждый узел имеет не более двух сыновей.

Бинарное дерево – это конечное множество элементов, которое либо пусто, либо содержит элемент (корень), связанный с двумя различными бинарными деревьями, называемыми левым и правым поддеревьями.
Каждый элемент бинарного дерева называется узлом.
Связи между узлами дерева называются его ветвями.
A – корень дерева
В – корень левого поддерева
С – корень правого поддерева
Способ представления бинарного дерева:

Деревья широко применяются в следующих задачах:
поиск в большом массиве неменяющихся данных
сортировка данных
вычисление арифметических выражений
оптимальное сжатие данных (метод Хаффмана)

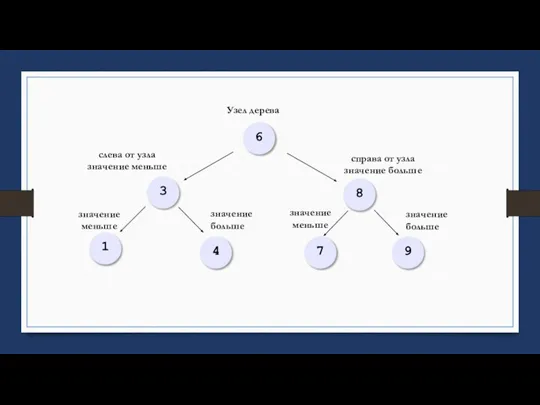
Перечислим важные свойства дерева, показанного на рисунке:
слева от узла – узлы с меньшими или равными ключами
справа от узла – узлы с большими или равными ключами
Дерево, обладающее такими свойствами, называется бинарным (двоичным) деревом поиска.

6
1
3
4
7
9
8
Узел дерева
слева от узла значение меньше
справа от узла значение больше
значение больше
значение больше
значение меньше
значение меньше

Что такое граф?
Граф — это набор узлов (вершин) и связей между ними (рёбер).
Информацию об узлах и связях графа обычно хранят в виде таблицы специального вида — матрицы смежности

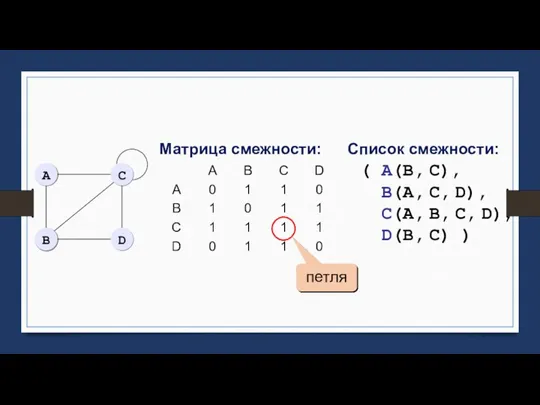
петля
Матрица смежности:
Список смежности:
( A(B, C), B(A, C, D), C(A, B, С, D), D(B, C) )

Единица на пересечении строки А и столбца В означает, что между узлами А и В есть связь.
Ноль указывает на то, что связи нет.
Матрица смежности симметрична относительно главной диагонали.
Единица на главной диагонали обозначает петлю — ребро, которое начинается и заканчивается в одной и той же вершине (в данном примере — в вершине С).
петля
Матрица смежности:

Строго говоря, граф — это математический объект, а не рисунок.
Его можно нарисовать на плоскости, но матрица смежности не даёт никакой информации о том, как именно следует располагать узлы друг относительно друга. Для таблицы, приведённой на предыдущем слайде, возможны такие варианты:

В рассмотренном примере все узлы связаны, т. е. между любой парой узлов существует путь — последовательность рёбер, по которым можно перейти из одного узла в другой. Такой граф называется связным.
Вспоминая материал предыдущего урока, можно сделать вывод, что дерево — это частный случай связного графа, в котором нет замкнутых путей — циклов.

Если для каждого ребра указано направление, то такой граф называют ориентированным.
Его рёбра называют дугами, а матрица смежности не всегда симметричная. Единица, стоящая на пересечении строки А и столбца В, говорит о том, что существует дуга из вершины А в вершину В
Матрица смежности:

Часто с каждым ребром связывают некоторое число — вес ребра. Это может быть, например, расстояние между городами или стоимость проезда. Такой граф называется взвешенным.
Информация о взвешенном графе хранится в виде весовой матрицы, содержащей веса рёбер.
Весовая матрица :
вес ребра

У взвешенного ориентированного графа весовая матрица может быть несимметрична относительно главной диагонали
Весовая матрица :

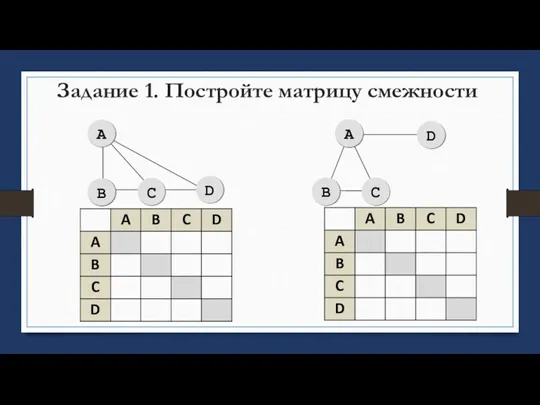
Задание 1. Постройте матрицу смежности

Задание 2. Постройте граф, как он и его матрица называются?

Домашнее задание
Задание 1. Постройте матрицы смежности или весовые матрицы для каждого графа:

Задание 2. Постройте граф, соответствующий матрице смежности