ТАиФЯ № 2 (МТ)

А́лан Мэ́тисон Тью́ринг
Alan Mathison Turing
Общепринято считать Алана Тьюринга отцом Общепринято считать Алана Тьюринга отцом информатики и теории Общепринято считать Алана Тьюринга отцом информатики и теории искусственного интеллекта.
английский математик,
логик, криптограф (Энигма)
«Алан Тьюринг - взломщик кодов и пионер информатики».
1912-1954

Премия Тьюринга (Turing Award) - самая престижная премия в самая престижная премия в информатике, вручаемая Ассоциацией вычислительной
техники за выдающийся научно-технический вклад в этой области.
В настоящее время премия спонсируется корпорациями Intel и Google и составляет 250 000 долларов США.
Лауреаты премии Тьюринга
Р. Хэмминг, Н. Вирт, Д. Кнут,
Э. Дейкстра , Д. Грэй, Д. Перл, Ч. Теккер…..

Символьные конструкции
Алфавит - любое конечное множество попарно различных знаков, называемых буквами (символами) этого алфавита.
Алфавит будем обозначать заглавными буквами, например:
Символом λ - обозначение пустого символа.

Слово в данном алфавите - любая конечная (в том числе и пустая) последовательность букв этого алфавита.
Слова обозначаются малыми греческими буквами.
Например:
α = algorithm - слово в алфавите А;
β = 1010100 - слово в алфавите В;
- слово в алфавите С.
Пустое слово обозначим Λ.

Длина слова α (обозначается |α| ) - это количество букв в слове.
Отношения и операции над словами
Равенство слов в алфавите А определяется индуктивно:
а) пустые слова равны;
б) если слово α равно слову β, то
α b = βb , где b - буква в алфавите А.

Если слово α является частью слова β в алфавите A, то слово α – подслово слова β (или слово α входит в слово β).
Например: в слове 1012011201 два вхождения слова 12, три вхождения слова 01, одиннадцать вхождений пустого слова Λ - перед первой, после последней букв и между всеми буквами.

Слово длины n , составленное из буквы а, повторенной n раз, будем обозначать
Например xyxxxyyyy = .

Классическая машина Тьюринга
Основные определения
Под машиной Тьюринга понимается гипотетическая (абстрактная) машина, состоящая из следующих частей:
1) потенциально бесконечной в обе стороны ленты, разбитой на ячейки, в каждой ячейке может быть записан только один символ из алфавита
а также пустой символ λ ;

2) УУ - управляющего устройства (рабочей головки), которое в каждый момент времени может находится в одном из состояний множества
В каждом из состояний головка размещается напротив ячейки и может считывать (обозревать) или записывать в нее букву из алфавита А.

Классическая машина Тьюринга
Часть ленты, в которой записаны буквы алфавита А - рабочая зона.
λ
a
1
...
a
j
...
a
k
λ
...
...
λ

Функционирование КМТ
состоит из последовательности элементарных шагов (тактов).
На каждом шаге выполняются следующие действия:
1) УУ считывает символ
2) в зависимости от своего состояния
и считанного символа ленты УУ вырабатывает символ
и записывает его в обозреваемую ячейку, возможно

3) УУ перемещается на одну ячейку вправо (R) , влево (L) или остается на месте (E);
4) УУ переходит в другое внутреннее состояние возможно
Состояние - начальное (МТ начинает работу),
- заключительное состояние.
При переходе в заключительное состояние машина останавливается.

Математическое описание КМТ
где А – внешний алфавит символов,
Q – алфавит внутренних состояний машины,
V – алфавит допустимых движений,
- начальное и заключительное состояния,
- функция переходов.

Способы описания КМТ:
- система команд (программа) ;
- функциональная таблица;
- диаграмма состояний (граф переходов).

Система команд (программа) КМТ
Совокупность команд вида:
называют системой команд или программой КМТ.
Порядок следования команд в программе не имеет принципиального значения

Система команд МТ
1) начальному шагу алгоритма ставится в соответствие начальное состояние
2) соседним шагам алгоритма соответствует переход в смежные состояния
3) циклы реализуются так, что последнее действие цикла должно соответствовать переходу в то состояние, которое соответствует началу цикла
4) последний шаг алгоритма - переход в заключительное состояние.

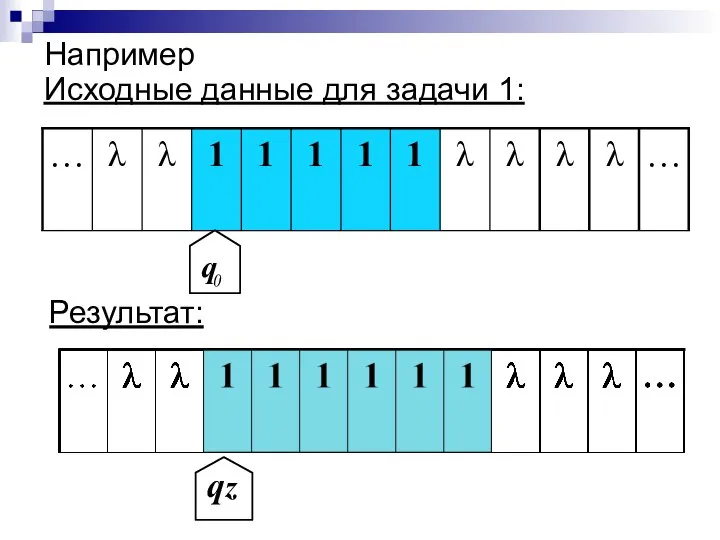
Построить МТ, вычисляющую функцию последователь (+1) в унарной системе счисления.
Задача 1.

Унарная (единичная) система счисления - положительная целочисленная система счисления с основанием, равным 1.
В качестве единственной «цифры»
используется «1» или черточка «/» или «|».
Число x в унарном коде

Например
Исходные данные для задачи 1:

Два варианта решения задачи 1
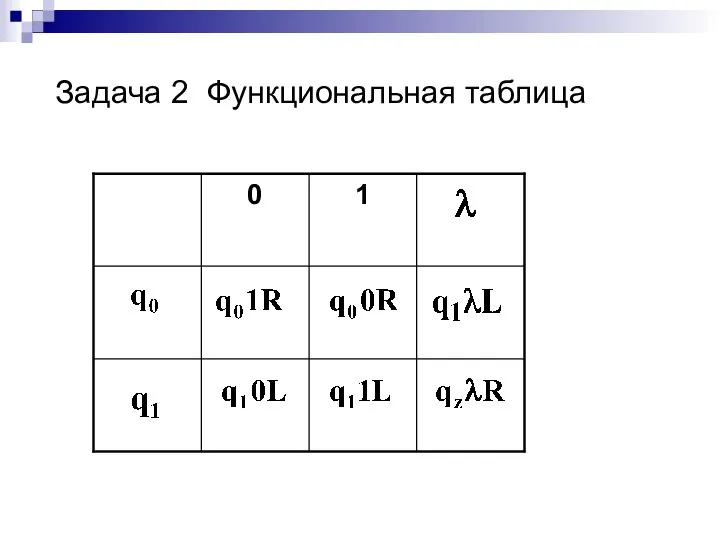
MT1 MT2

Задача 2
Построить МТ, реализующую инвертирование числа в двоичной системе счисления

1) УУ стоит над первым значащим символом слева, в начале рабочей зоны.
2) На след. такте МТ, не меняя своего состояния, заменяет символ 0 на 1 и наоборот и сдвигается вправо на один символ.
3) После просмотра всей цепочки УУ обозревает символ, указывающий на пустую ячейку. В этом случае МТ переходит в новое состояние и сдвигается влево на один символ.

4) На последующих тактах УУ не меняя своего состояния и обозреваемого символа, перемещается влево до пустой ячейки.
5) Встретив пустую ячейку, МТ переходит в заключительное состояние и перемещается вправо на один символ, переходя в заключительную стандартную конфигурацию.

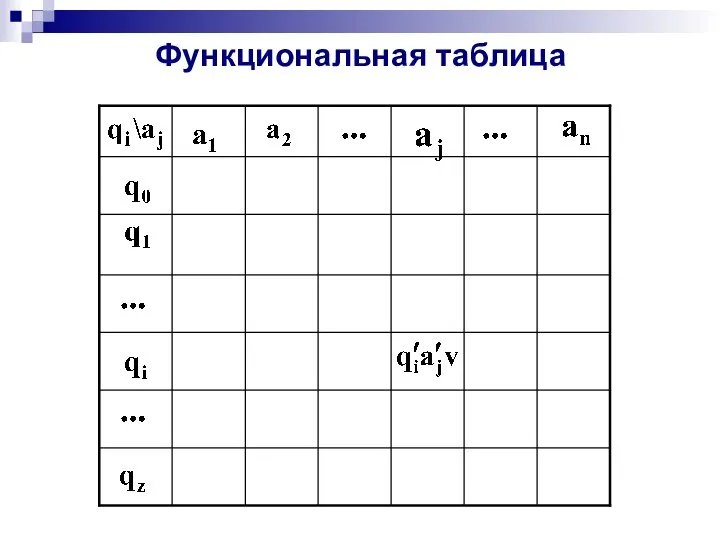
Функциональная таблица

Каждому состоянию МТ соответствует строка в функциональной таблице.
Каждому символу из входного алфавита столбец.
В клетках таблицы на пересечении строки и столбца записывается действие (правая часть команды), которое выполняется в этом состоянии, при данном обозреваемом символе.

Задача 2 Функциональная таблица

Задача 3
Построить МТ, реализующую сложение двух чисел в унарном коде .
Начальная конфигурация:
Конечная конфигурация:
т.е. сложение фактически сводится к приписыванию числа b к числу a .
Для этого первая 1 стирается, а * заменяется на 1.

Приведем описание МТ в виде функциональной таблицы

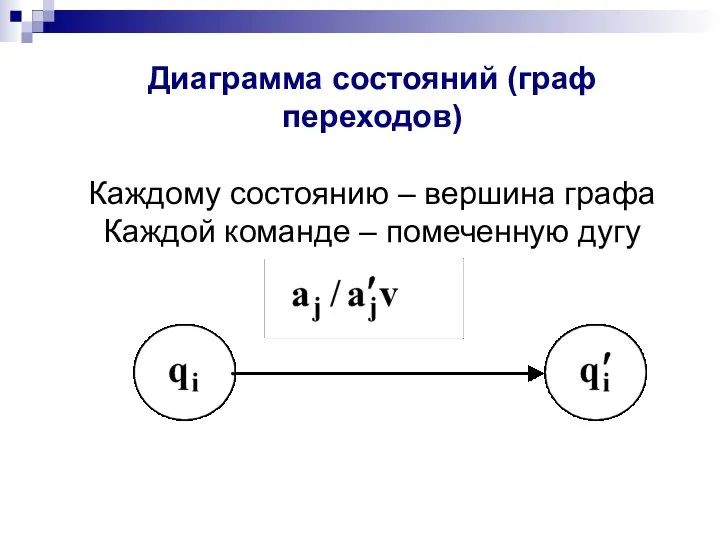
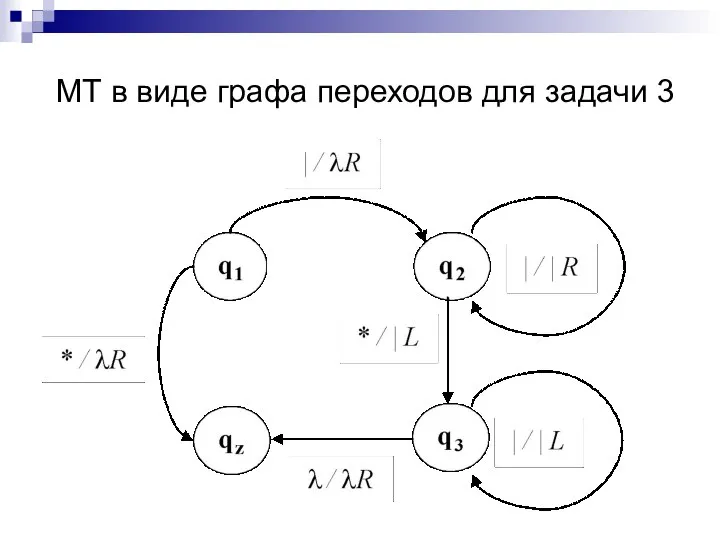
Диаграмма состояний (граф переходов)
Каждому состоянию – вершина графа
Каждой команде – помеченную дугу

МТ в виде графа переходов для задачи 3

Описание МТ в виде системы команд для задачи 3

Полное состояние МТ – конфигурация:
состояние рабочей зоны - распределение букв по ячейкам ленты, положение рабочей головки и внутреннее состояние УУ.
Конфигурация в такте t:
где
- подслово слева от обозреваемой ячейки,
- символ в обозреваемой ячейке,
- подслово справа от обозреваемой ячейки.

Начальная конфигурация и конечная называются стандартными:
МТ начинает и заканчивает свою работу в таком положении, когда УУ обозревает самый левый символ рабочей зоны ленты.

Функционирование МТ – последовательная смена ее конфигураций в соответствии с функцией перехода δ – протокол работы МТ:

Говорят, что МТ применима к слову α, если она переводит
начальную конфигурацию
за конечное число шагов в некоторую заключительную конфигурацию
В этом случае МТ вычисляет словарную функцию f(α).
Если значение f(α) не определено, то МТ работает бесконечно.

Числовая функция
вычислима по Тьюрингу, если существует МТ, которая переводит конфигурацию
в конфигурацию
когда ,
или работает бесконечно, когда
не определена.

Тезис Черча для МТ:
любая вычислимая в интуитивном смысле функция вычислима на машине Тьюринга.
Класс функций вычислимых на МТ совпадает с классом ЧРФ.

Задача 4
Построить МТ, вычисляющую функцию последователь (+1) в двоичной системе счисления.

Движение вправо -
Движение влево -
Добавление 1 -
Протоколы работы МТ для трех тестовых примеров:
110+1=111
101+1 =110
111+1=1000