- Главная
- Информатика
- Теория чисел. Задание 19

Содержание
- 2. Теория. На 2: последняя цифра числа четная. Например, 2098 На 3: сумма цифр числа делится на
- 3. На 8: три последние цифры числа нули или образуют число, делящееся на 8. Например, 12345112 На
- 4. Приведите пример трехзначного наименьшего натурального числа меньшего 500, которое при делении на 8 и 5 дает
- 5. Вычеркните из числа 21462143 три цифры так, чтобы получившееся число делилось на 12. В ответ укажите
- 6. Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из
- 8. Скачать презентацию
Слайд 2Теория.
На 2: последняя цифра числа четная. Например, 2098
На 3: сумма цифр числа
Теория.
На 2: последняя цифра числа четная. Например, 2098
На 3: сумма цифр числа

На 4: две последние цифры числа нули или образуют число, делящееся на 4. Например, 123416
На 5: последняя цифра числа 0 или 5. Например, 12060
На 6: число должно делиться на 3 и на 2, а это можно проверить с помощью признаков делимости на 2 и на 3. Например, 11142
Слайд 3На 8: три последние цифры числа нули или образуют число, делящееся на
На 8: три последние цифры числа нули или образуют число, делящееся на

На 9: сумма цифр числа делится на 9. Например, 5517
На 11: сумма цифр, стоящих на четных местах, отличается от суммы цифр, стоящих на нечетных местах, на число, которое делится на 11. Например, 72457
На 25: число оканчивается на 00, 25, 50 или 75. Например, 250
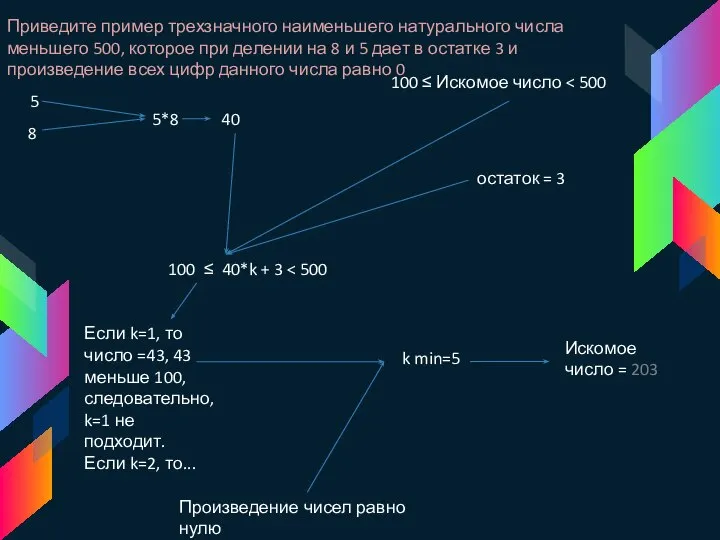
Слайд 4Приведите пример трехзначного наименьшего натурального числа меньшего 500, которое при делении на
Приведите пример трехзначного наименьшего натурального числа меньшего 500, которое при делении на
5
8
5*8
40
100 ≤ Искомое число < 500
100 ≤ 40*k + 3 < 500
остаток = 3
Если k=1, то число =43, 43 меньше 100, следовательно, k=1 не подходит.
Если k=2, то...
k min=5
Искомое число = 203
Произведение чисел равно нулю
Слайд 5Вычеркните из числа 21462143 три цифры так, чтобы получившееся число делилось на
Вычеркните из числа 21462143 три цифры так, чтобы получившееся число делилось на

Число делится на 12
Делится на 3 и на 4 одновременно
Сумма цифр числа делится на 3
Две последние цифры числа нули или образуют число, делящееся на 4
3 не может стоять в конце
Вычеркиваем. Получаем 2146214
14 не делится на 4. Вычеркнем 1. Остается 214624
Сумма цифр = 19. Делится на 3 с остатком 1. Вычеркнем 1
Получаем 24624, что и будет ответом
Слайд 6Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе
Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе

Число делится на 5, значит, его последняя цифра или 0, или 5. Но так как при записи в обратном порядке цифры также образуют четырёхзначное число, то эта цифра 5, потому что число не может начинаться с 0. Пусть число = [abc5] => [5cba] = это же число наоборот. 0 < a ≤ 9, 0 ≤ b ≤ 9, 0 ≤ c ≤ 9
Запишем уравнение в таком виде:
1000a + 100b + 10c + 5 – (5*1000 + 100c + 10b + a) = 4536
Решаем:
1000a + 100b + 10c + 5 – 5000 – 100c - 10b – a = 4536
999a + 90b – 90c - 4995 = 4536
(999a – 4995) + (90b-90c) = 4536
999(a – 5) + 90(b – c) = 4536 |:9
111(a – 5) + 10(b – c) = 504
Анализируя данное уравнение, приходим к выводу a = 9
444 + 10(b – c) = 504
10(b – c) = 60
b – c = 6
Методом подбора (с = 0 и b = 6, с = 1 и b = 7 и тд) находим все ответы: 9605, 9715, 9825, 9935
 Знакомство с системой компьютерной математики
Знакомство с системой компьютерной математики Операционные системы
Операционные системы Управление программным обеспечением
Управление программным обеспечением Poddotazy
Poddotazy Как создать страницу компании в Google
Как создать страницу компании в Google Форматирование текста (шрифт 2). Web-проектирование
Форматирование текста (шрифт 2). Web-проектирование Формулы, применяющиеся в Excel
Формулы, применяющиеся в Excel Моделирование — это метод познания, состоящий в создании и исследовании моделей
Моделирование — это метод познания, состоящий в создании и исследовании моделей Интерактивный путеводитель
Интерактивный путеводитель Препятствия диджитализации страхования в России и возможные пути их преодоления
Препятствия диджитализации страхования в России и возможные пути их преодоления Linux – маршрутизация, NAT, DHCP
Linux – маршрутизация, NAT, DHCP Programming on Python. Lecture 7
Programming on Python. Lecture 7 Котельная Спортлагерь Олимп
Котельная Спортлагерь Олимп Администратор баз данных областное автономное учреждение социального обслуживания
Администратор баз данных областное автономное учреждение социального обслуживания Скандальные домены
Скандальные домены Описательные статистики
Описательные статистики Microservices and monolith
Microservices and monolith Диалоги в поселке
Диалоги в поселке Жизненный цикл информационной системы
Жизненный цикл информационной системы 6-12-1-grafiki-i-diagrammy
6-12-1-grafiki-i-diagrammy Массивы
Массивы Информационно-коммуникационные технологии обучения (ИКТ)
Информационно-коммуникационные технологии обучения (ИКТ) Видеотехнологии. Кодирование видео (теория)
Видеотехнологии. Кодирование видео (теория) programmirovanie_l5-2016
programmirovanie_l5-2016 Пэкмен. Обзор. Скайрим – моя жизнь
Пэкмен. Обзор. Скайрим – моя жизнь Принцип программного управления компьютером. Лекция № 2
Принцип программного управления компьютером. Лекция № 2 Основы языка Visual Basic. Функции
Основы языка Visual Basic. Функции Хронометраж для соревнований
Хронометраж для соревнований