Содержание
- 2. Характер и достижения античной науки Научное познание как построение рациональных моделей познаваемых объектов Платон: постижение мировой
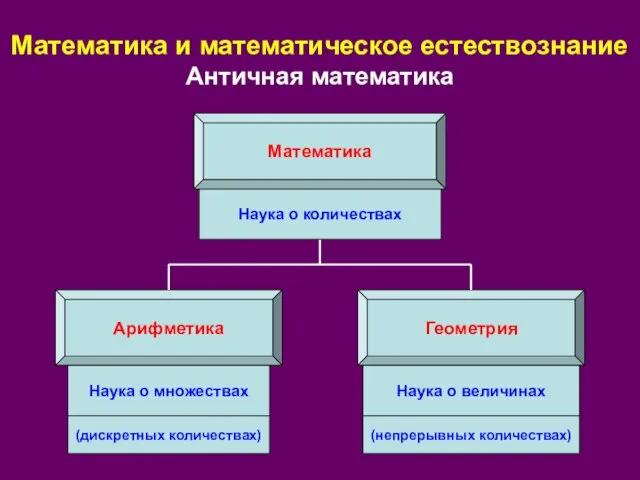
- 3. Математика Арифметика Геометрия Наука о множествах Наука о величинах (дискретных количествах) (непрерывных количествах) Наука о количествах
- 4. Математика и математическое естествознание Античная астрономия
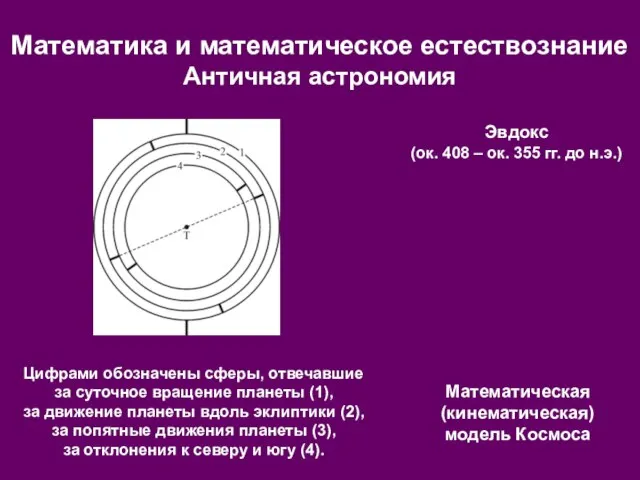
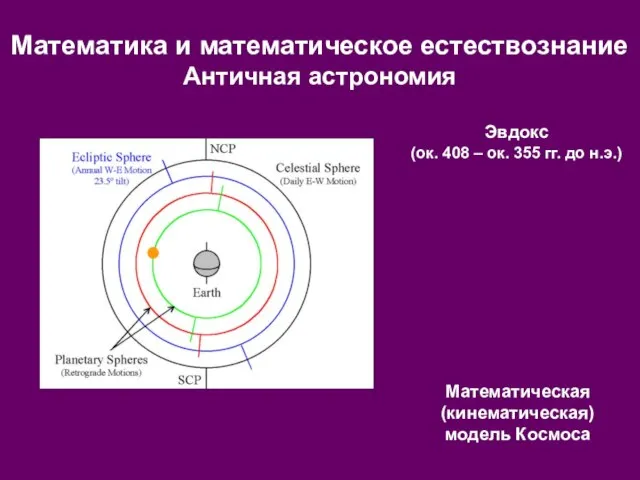
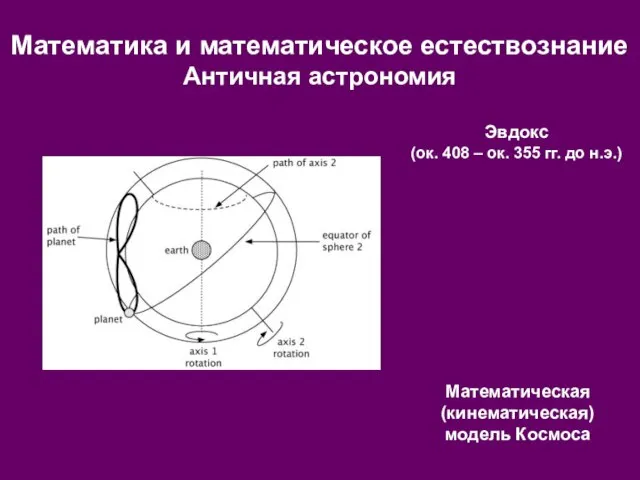
- 5. Математика и математическое естествознание Античная астрономия Эвдокс (ок. 408 – ок. 355 гг. до н.э.) Математическая
- 6. Математика и математическое естествознание Античная астрономия Эвдокс (ок. 408 – ок. 355 гг. до н.э.) Математическая
- 7. Математика и математическое естествознание Античная астрономия Эвдокс (ок. 408 – ок. 355 гг. до н.э.) Математическая
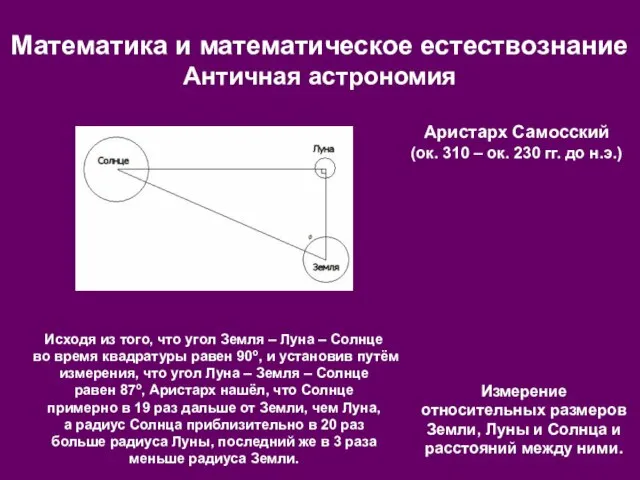
- 8. Математика и математическое естествознание Античная астрономия Аристарх Самосский (ок. 310 – ок. 230 гг. до н.э.)
- 9. Математика и математическое естествознание Античная астрономия Аристарх Самосский (ок. 310 – ок. 230 гг. до н.э.)
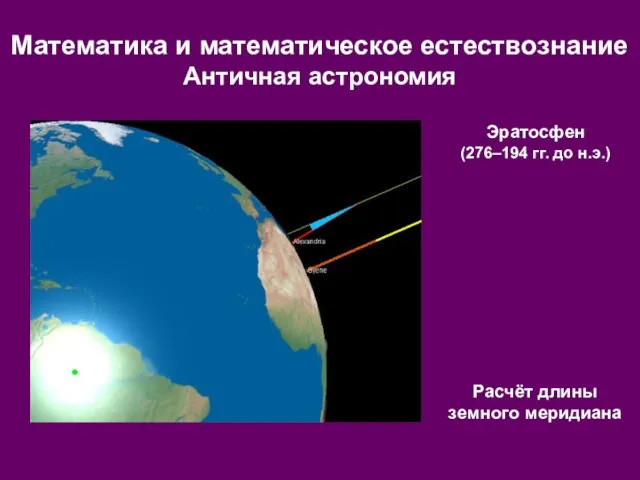
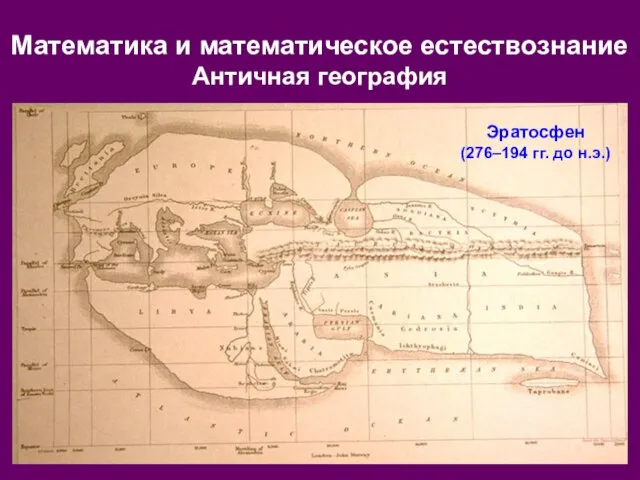
- 10. Эратосфен (276–194 гг. до н.э.) Расчёт длины земного меридиана Математика и математическое естествознание Античная астрономия
- 11. Дуга меридиана между Сиеной и Александрией была определена как 1/50 круга, т.е. 7,20. Расстояние между Сиеной
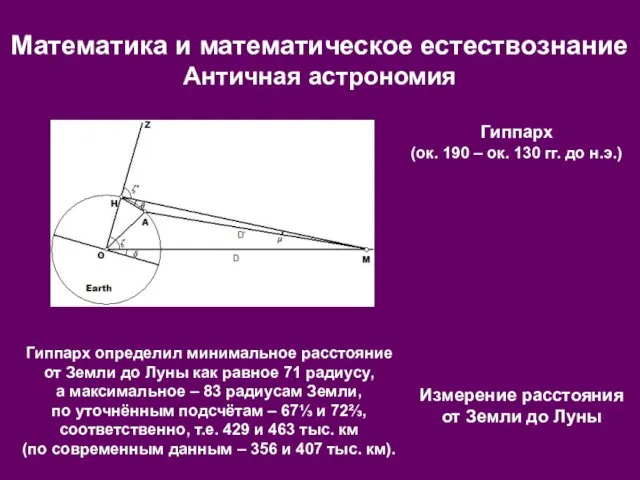
- 12. Гиппарх (ок. 190 – ок. 130 гг. до н.э.) Измерение расстояния от Земли до Луны Гиппарх
- 13. Клавдий Птолемей (ок. 90 – ок. 168 гг. н.э.) Геоцентрическая система Космоса Схема движения планеты вокруг
- 14. Математика и математическое естествознание Античная география Эратосфен (276–194 гг. до н.э.)
- 16. Скачать презентацию




 Памятники г. Смоленска
Памятники г. Смоленска Завоевание Римом Средиземноморья
Завоевание Римом Средиземноморья Крещение Руси
Крещение Руси Основные черты западноевропейского феодализма
Основные черты западноевропейского феодализма Мы помним, мы гордимся
Мы помним, мы гордимся Урок гражданственности и духовности Донбасса
Урок гражданственности и духовности Донбасса Проект Вахта памяти к 70-летию со Дня Великой Победы в ВОВ
Проект Вахта памяти к 70-летию со Дня Великой Победы в ВОВ История создания вооруженных сил РФ
История создания вооруженных сил РФ Тауэрские вороны
Тауэрские вороны Педагогика Античности
Педагогика Античности Положение основных слоев общества. Россия во второй половине XIX в
Положение основных слоев общества. Россия во второй половине XIX в История земельного кадастра и бонитировки почв в россии
История земельного кадастра и бонитировки почв в россии Просвещенный абсолютизм Екатерины II
Просвещенный абсолютизм Екатерины II Семейные истории великой победы. Кировская область г. Кирс. Осколкова Наталья Михайловна
Семейные истории великой победы. Кировская область г. Кирс. Осколкова Наталья Михайловна Презентация на тему Пифагорейская школа
Презентация на тему Пифагорейская школа  The Great Patriotic War of 1941-1945
The Great Patriotic War of 1941-1945 27 января — День полного снятия блокады Ленинграда
27 января — День полного снятия блокады Ленинграда Великое стояние на реке Угре
Великое стояние на реке Угре Триумф человеческого разума (Тест)
Триумф человеческого разума (Тест) Искусство скифов
Искусство скифов карточки 2
карточки 2 Манифест 17 октября 1905 года
Манифест 17 октября 1905 года Хэллуин
Хэллуин Новейшая история зарубежных стран
Новейшая история зарубежных стран Зарождение полководческого таланта Г.К.Жукова на этапе командования эскадроном и полком
Зарождение полководческого таланта Г.К.Жукова на этапе командования эскадроном и полком Modes de vie
Modes de vie Переднеазиатское крыло Пергамского музея в Берлине
Переднеазиатское крыло Пергамского музея в Берлине Дети - герои войны
Дети - герои войны