Содержание
- 2. Прямая на плоскости
- 3. Определение. Уравнением линии на плоскости называется уравнение, которому удовлетворяют координаты и любой точки данной линии и
- 4. Теорема. Всякое уравнение первой степени где А и В не обращаются в нуль одновременно, представляет собой
- 5. Уравнение прямой, проходящей через точку перпендикулярно вектору
- 6. Введем следующие понятия. Вектор, перпендикулярный прямой будем называть нормалью прямой и обозначать Итак, . Вектор, параллельный
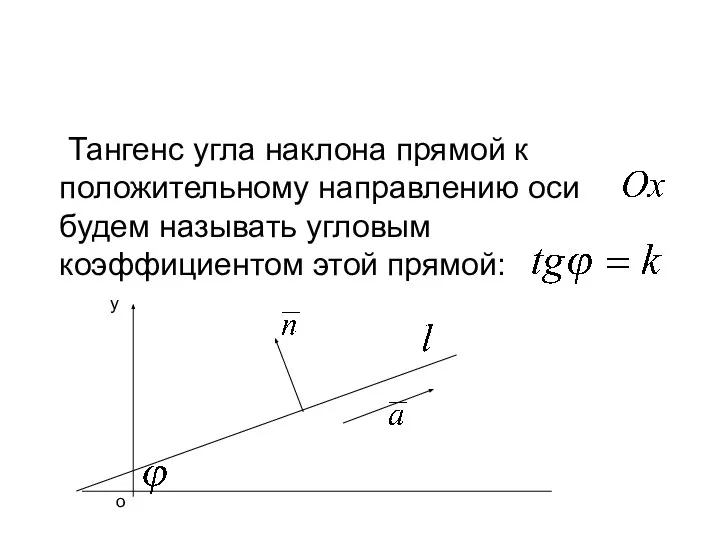
- 7. Тангенс угла наклона прямой к положительному направлению оси будем называть угловым коэффициентом этой прямой: о х
- 8. Пусть точка лежит на прямой. Точка -произвольная точка прямой. .
- 9. Тогда скалярное произведение
- 10. Получили уравнение прямой, проходящей через заданную точку, перпендикулярно данному вектору:
- 11. Общее уравнение прямой Из предыдущего уравнения легко получаем общее уравнение прямой
- 12. Каноническое уравнение прямой
- 13. Пусть и
- 14. Тогда из условия коллинеарности векторов и получаем каноническое, т. е. простейшее уравнение прямой:
- 15. Пример Написать уравнения прямых, проходящих через точку параллельно и перпендикулярно вектору . Первое уравнение и второе
- 16. Уравнение прямой, проходящей через две точки
- 17. Пусть
- 18. Координаты этих векторов пропорциональны: Получили уравнение прямой, проходящей через две точки.
- 19. Параметрические уравнения прямой Приравняем обе части соотношения к t. Получим параметрические уравнения прямой
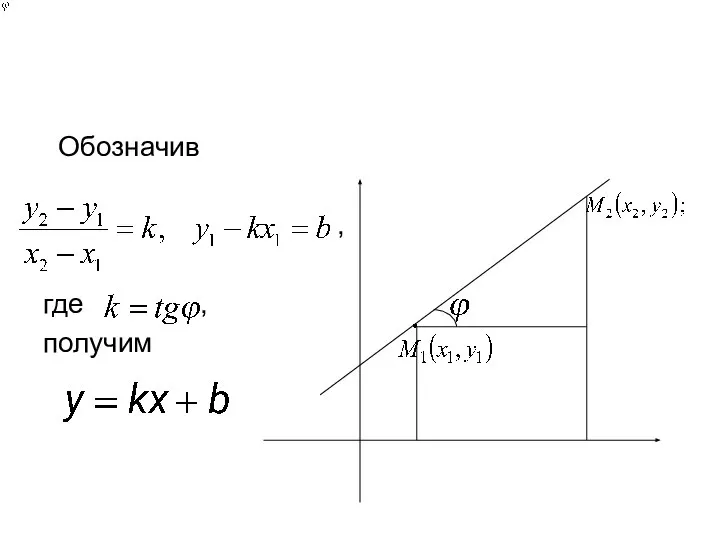
- 20. Уравнение прямой с угловым коэффициентом Преобразуем уравнение к виду
- 21. Обозначив , где , получим
- 22. Уравнение прямой ,проходящей через точку Пусть точка лежит на прямой . Тогда Вычтем из первого второе
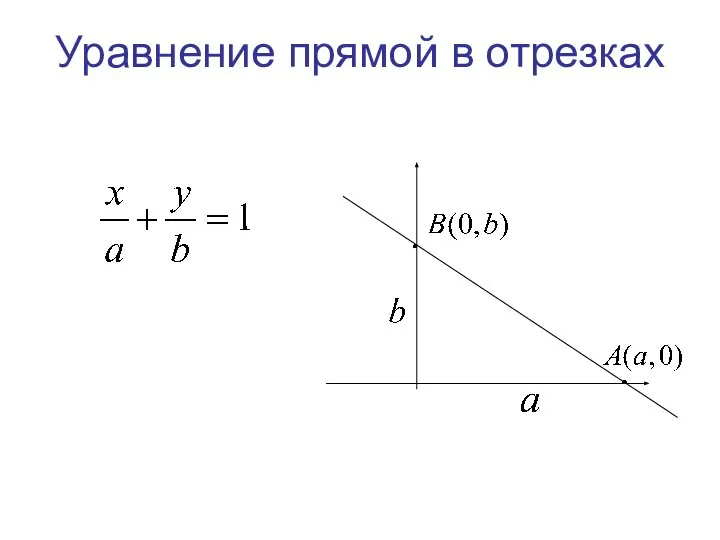
- 23. Уравнение прямой в отрезках
- 24. Взаимное расположение прямых
- 25. Угол между двумя прямыми Пусть две прямые заданы общими уравнениями
- 26. Тогда угол между этими прямыми равен углу между их нормалями , т. е.
- 27. Пусть даны прямые
- 28. Тогда
- 29. Условия параллельности Прямые параллельны тогда и только тогда, когда выполняется одно из двух условий ( в
- 30. Условие перпендикулярности
- 31. Расстояние от точки до прямой Расстояние от точки до прямой находят по формуле .
- 33. Скачать презентацию






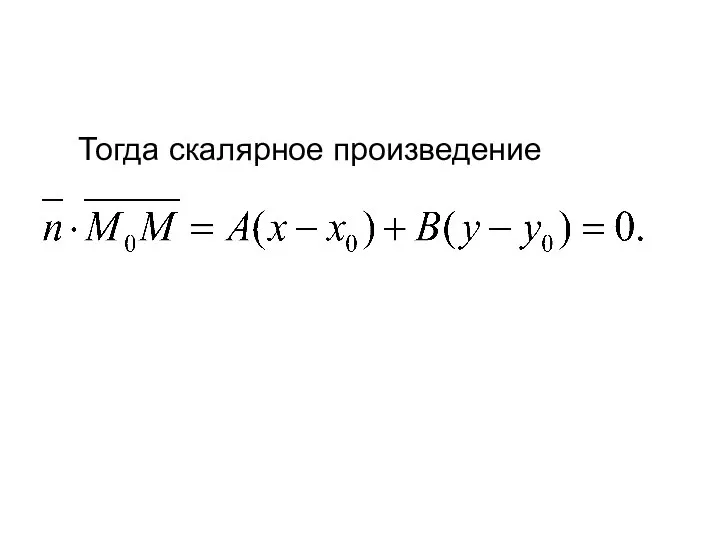
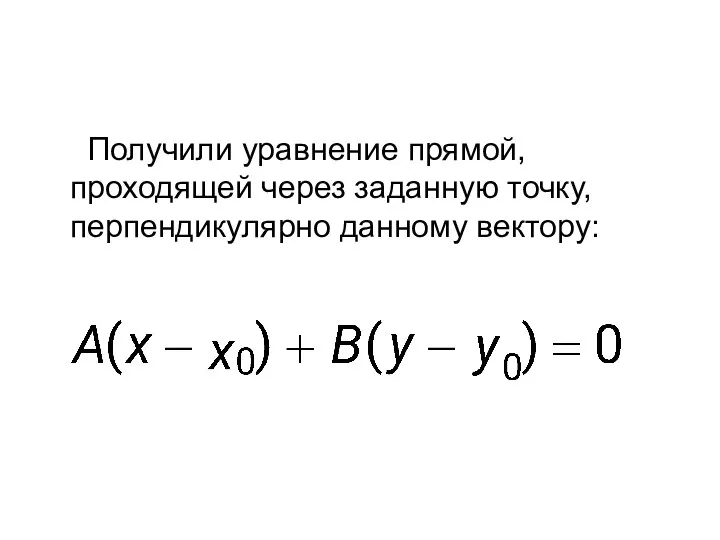


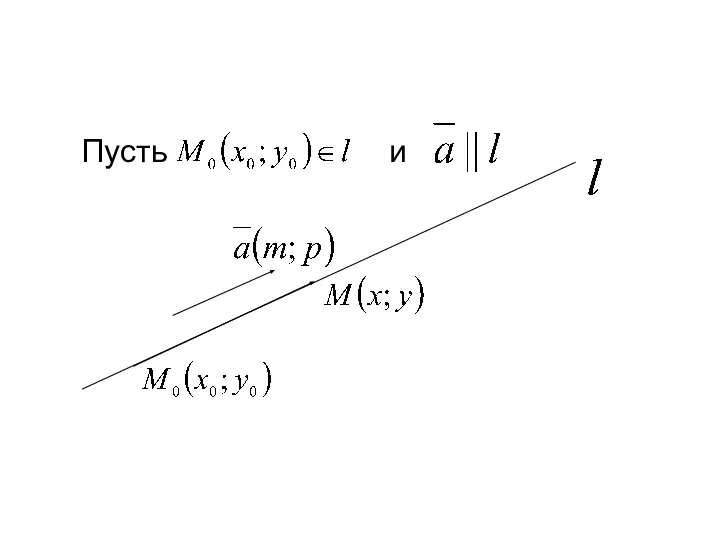



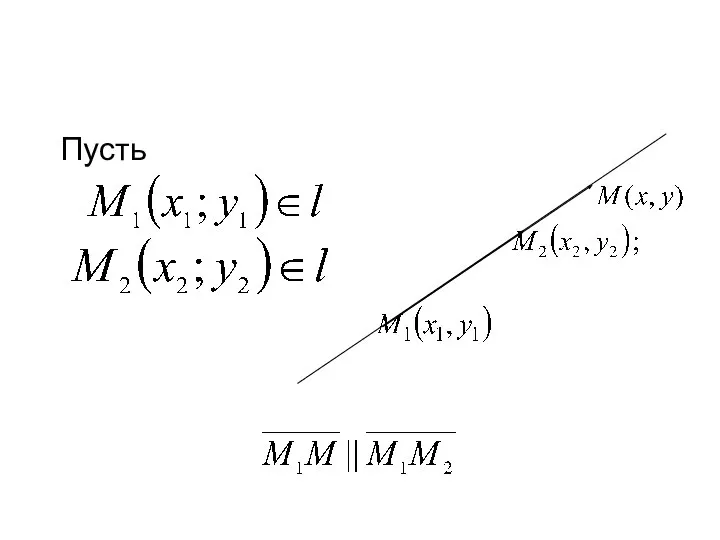








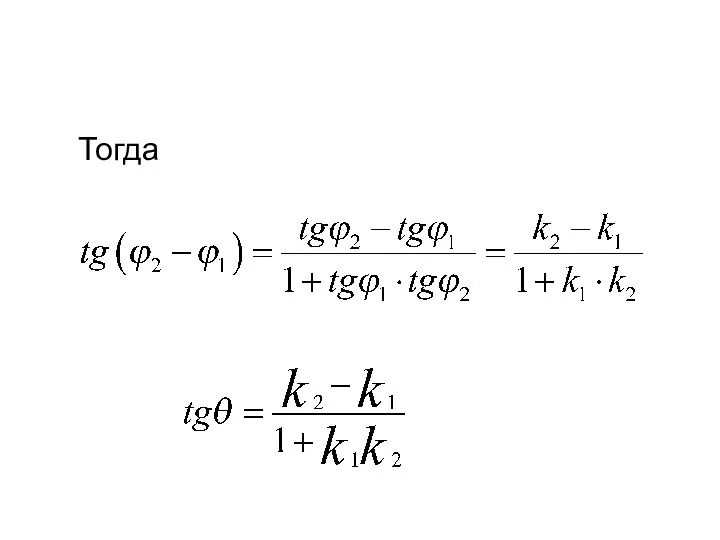



 Решение задач ЕГЭ по тригонометрии
Решение задач ЕГЭ по тригонометрии Решение практических задач с помощью арифметической прогрессии
Решение практических задач с помощью арифметической прогрессии Презентация на тему Лобачевский Николай Иванович
Презентация на тему Лобачевский Николай Иванович  Умножение многочлена на многочлен
Умножение многочлена на многочлен Перпендикулярные прямые
Перпендикулярные прямые Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Сложение и вычитание трёхзначных чисел
Сложение и вычитание трёхзначных чисел Зачем изучать математику?
Зачем изучать математику? Методы решения экстремальных задач
Методы решения экстремальных задач Решение неравенств
Решение неравенств Метрология. Стандартизация
Метрология. Стандартизация Решение тригонометрических уравнений
Решение тригонометрических уравнений Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4
Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4 Викторина по математике Путешествие в страну Любознательных
Викторина по математике Путешествие в страну Любознательных Вынесение множителя из - под знака корня. Внесение множителя под знак корня
Вынесение множителя из - под знака корня. Внесение множителя под знак корня Интеллектуальная игра Самый умный. Информатика. Математика
Интеллектуальная игра Самый умный. Информатика. Математика Математический маятник. Измерения
Математический маятник. Измерения Матрицы
Матрицы Движение в математике
Движение в математике Решение задач по геометрии
Решение задач по геометрии Сокращение дробей
Сокращение дробей Готовимся к ЕГЭ. Базовый уровень
Готовимся к ЕГЭ. Базовый уровень Случаи вычитания
Случаи вычитания Цифры - прописи. Анимированный плакат
Цифры - прописи. Анимированный плакат Радианная мера угла. Поворот точки вокруг начала координат
Радианная мера угла. Поворот точки вокруг начала координат Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша
Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша Сложение в пределах 20
Сложение в пределах 20 Квадратные неравенства
Квадратные неравенства