Применение тригонометрии в геометрических задачах

1.1 ПРОТОТИП №27327. 1 СПОСОБ РЕШЕНИЯ
В треугольнике ABC АС=ВС=27, AH — высота,
Найдите BH.
A
B
C
Н
Р
1 способ решения:
27
27
18
Ответ: 30
18√5
12√5
Смотри 2 способ решения:
∆ АВС - равнобедренный
СР – высота в равнобедренном треугольнике.
┌
Используем теорему Пифагора для прямоугольного ∆СРВ :
По теореме
Пифагора:
СВ˂НВ ═> ∆АВС - тупоугольный

1.1 ПРОТОТИП №27327. 2 СПОСОБ РЕШЕНИЯ
В треугольнике ABC АС=ВС=27, AH — высота,
Найдите BH.
A
B
C
Н
Р
2 способ решения:
27
27
18√5
Ответ: 30
Смотри 3 способ решения:
СВ˂НВ ═> ∆АВС - тупоугольный

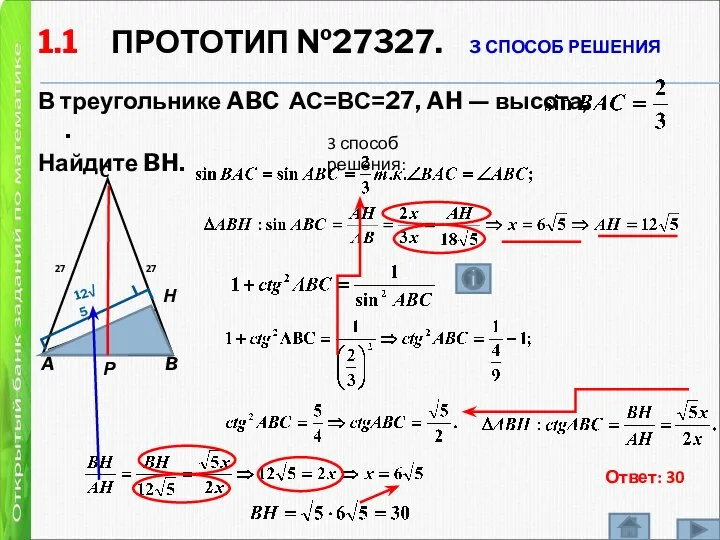
1.1 ПРОТОТИП №27327. 3 СПОСОБ РЕШЕНИЯ
В треугольнике ABC АС=ВС=27, AH — высота, .
Найдите BH.
3 способ решения:
C
A
B
Н
Р
27
27
12√5
C
Ответ: 30

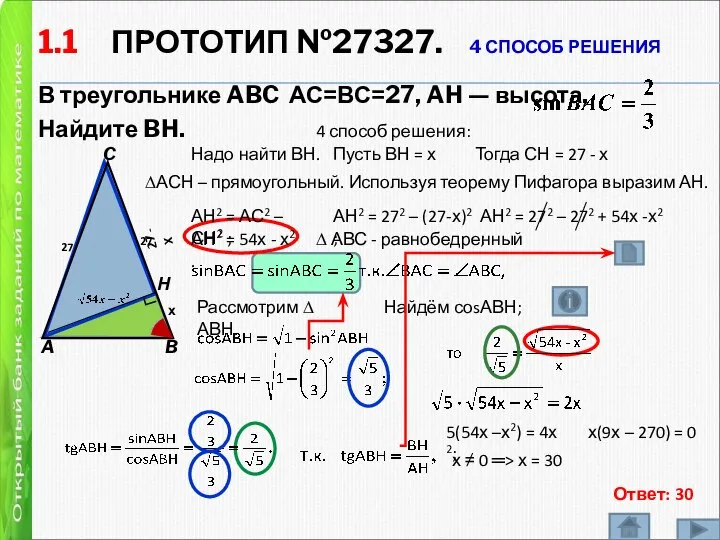
1.1 ПРОТОТИП №27327. 4 СПОСОБ РЕШЕНИЯ
В треугольнике ABC АС=ВС=27, AH — высота,
Найдите BH.
A
B
C
Н
4 способ решения:
27
27
Ответ: 30
∆ АВС - равнобедренный
┌
Надо найти ВН. Пусть ВН = х
х
Тогда СН = 27 - х
27 - х
∆АСН – прямоугольный. Используя теорему Пифагора выразим АН.
АН2 = АС2 – СН2 ;
АН2 = 272 – (27-х)2 ;
АН2 = 272 – 272 + 54х -х2 ;
АН2 = 54х - х2 .
Рассмотрим ∆ АВН.
Найдём соsАВН;
5(54х –х2) = 4х 2;
х(9х – 270) = 0
х ≠ 0 ═> х = 30

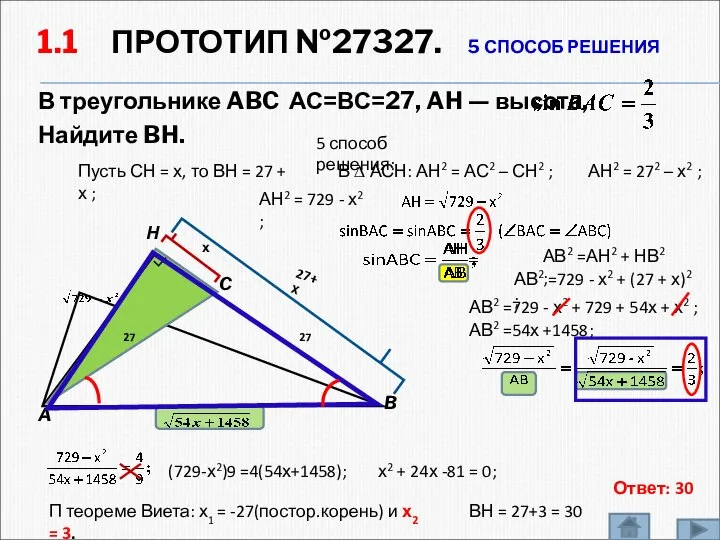
1.1 ПРОТОТИП №27327. 5 СПОСОБ РЕШЕНИЯ
В треугольнике ABC АС=ВС=27, AH — высота,
Найдите BH.
A
B
C
Н
5 способ решения:
27
Ответ: 30
┌
х
27+х
Пусть СН = х, то ВН = 27 + х ;
В ∆ АСН: АН2 = АС2 – СН2 ;
АН2 = 272 – х2 ;
АН2 = 729 - х2 ;
АВ2 =АН2 + НВ2 ;
АВ2 =729 - х2 + (27 + х)2 ;
АВ2 =729 - х2 + 729 + 54х + х2 ;
АВ2 =54х +1458;
27
(729-х2)9 =4(54х+1458);
х2 + 24х -81 = 0;
П теореме Виета: х1 = -27(постор.корень) и х2 = 3.
ВН = 27+3 = 30

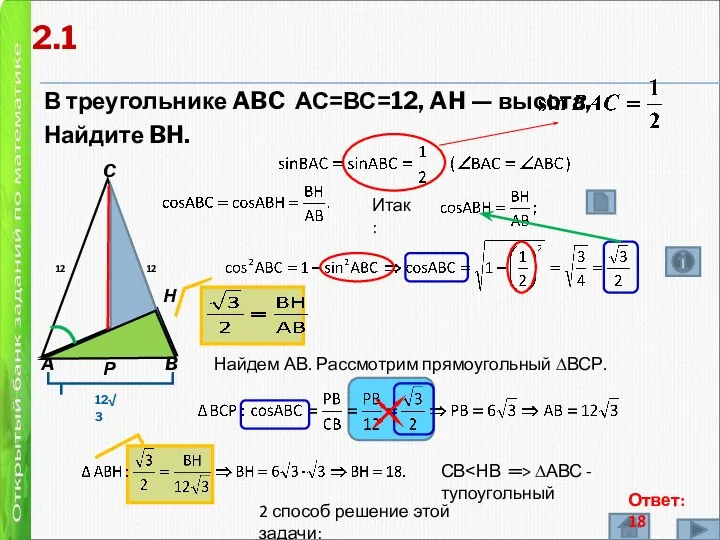
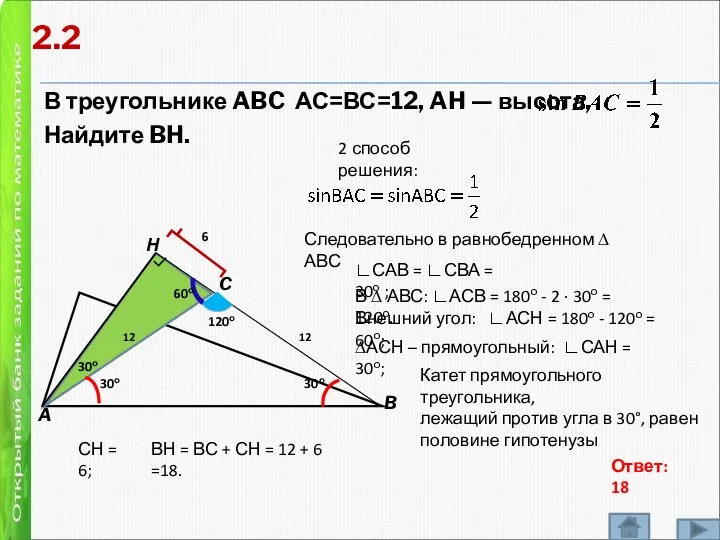
2
В треугольнике ABC АС=ВС=12, AH — высота,
Найдите BH.
A
B
C
Н
Р
12
12
12√3
Ответ: 18
Итак:
Найдем АВ. Рассмотрим прямоугольный ∆ВСР.
СВ˂НВ ═> ∆АВС - тупоугольный
2 способ решение этой задачи:
2.1

В треугольнике ABC АС=ВС=12, AH — высота,
Найдите BH.
A
B
C
Н
12
┌
12
Следовательно в равнобедренном ∆ АВС
∟САВ = ∟СВА = 30о ;
30о
30о
В ∆ АВС: ∟АСВ = 180о - 2 ∙ 30о = 120о.
120о
Внешний угол: ∟АСН = 180о - 120о = 60о;
60о
∆АСН – прямоугольный: ∟САН = 30о;
30о
Катет прямоугольного треугольника,
лежащий против угла в 30°, равен
половине гипотенузы
6
СН = 6;
ВН = ВС + СН = 12 + 6 =18.
Ответ: 18
2 способ решения:
2.2

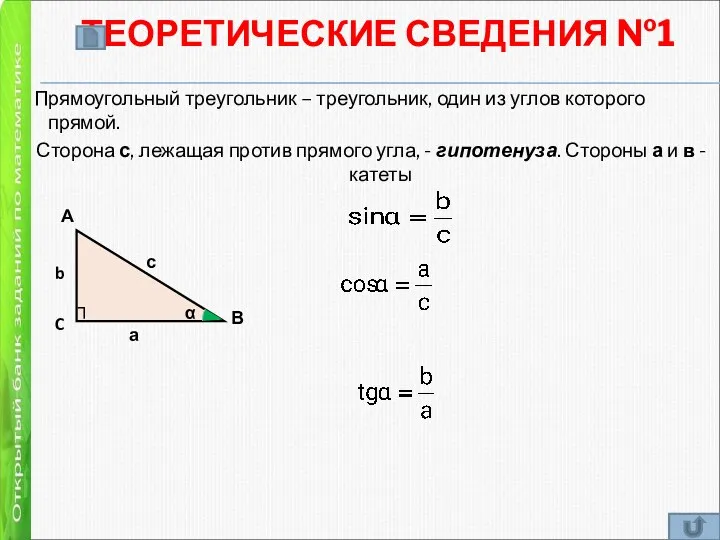
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №1
Прямоугольный треугольник – треугольник, один из углов которого прямой. Сторона с, лежащая против прямого угла, - гипотенуза. Стороны а и в - катеты
C
А
В
α
с
а
b
┐

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №2
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике высота, проведенная к основанию, является и медианой, и биссектрисой.
А
Р
С
В
СР – высота, медиана, биссектриса.
Медиана треугольника, проведенная из данной вершины - отрезок прямой, соединяющий эту вершину с серединой противолежащей стороны треугольника
Высота СР разделила ∆ АВС на два равных
прямоугольных треугольника

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №3
Основное тригонометрическое тождество
1.
2.