dz

Задачи урока:
Вспомнить и сформулировать определения возрастающей и убывающей функции; монотонности функции.
Исследовать функции на монотонность.

повторение
Дать определение числовой функции.
Что такое область определения функции?
Что такое область значений функции?
Перечислите способы задания функции.

Выполните:
1.18

Обратите внимание: во всех определениях фигурирует числовое
множество X, являющееся частью области определения функции: X с D(f).

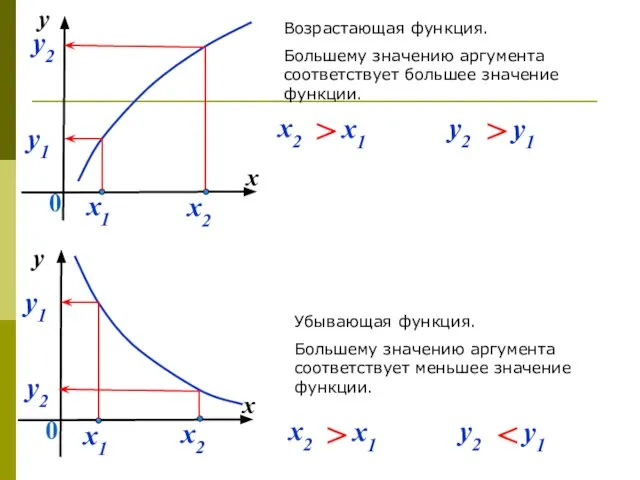
Геометрическое истолкование понятий возрастания или убывания функции:
двигаясь по графику возрастающей функции слева направо, мы как
бы поднимаемся в горку
двигаясь по графику убывающей функции слева направо, как бы спускаемся с горки

y
x
0
y2
Убывающая функция.
Большему значению аргумента соответствует меньшее значение функции.
Возрастающая функция.
Большему значению аргумента соответствует большее значение функции.
>
>
>
<

Монотонная функция
- общее название для терминов «возрастающая функция», «убывающая функция»

Исследование функции на монотонность
- исследование функции на возрастание или убывание.

Свойства числовых неравенств.

Докажите, что функция возрастает.
Возьмем произвольные значения
аргумента
Пусть
По свойствам числовых неравенств
значит функция возрастает