Содержание
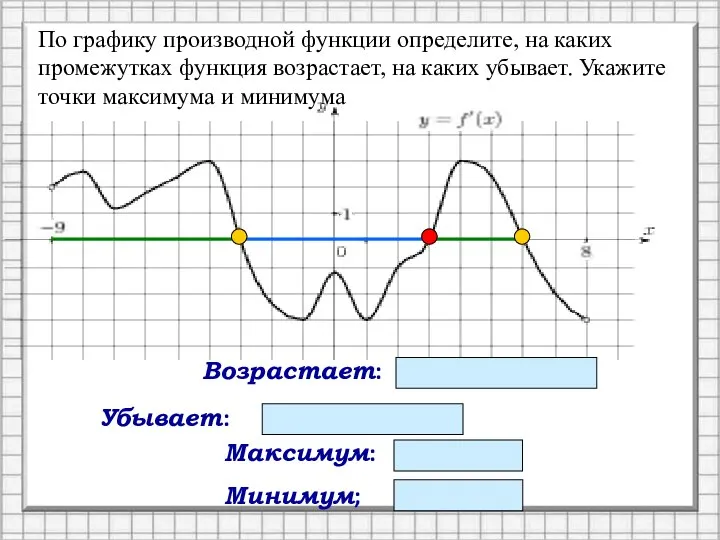
- 2. Максимум: - 3; 6 Минимум; 3 Возрастает: (-9;-3) и (3;6) Убывает: (-3;3) По графику производной функции
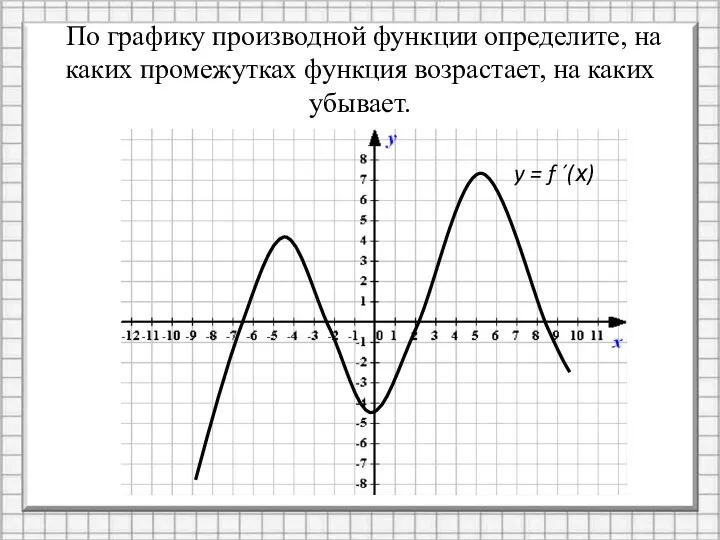
- 3. По графику производной функции определите, на каких промежутках функция возрастает, на каких убывает. y = f
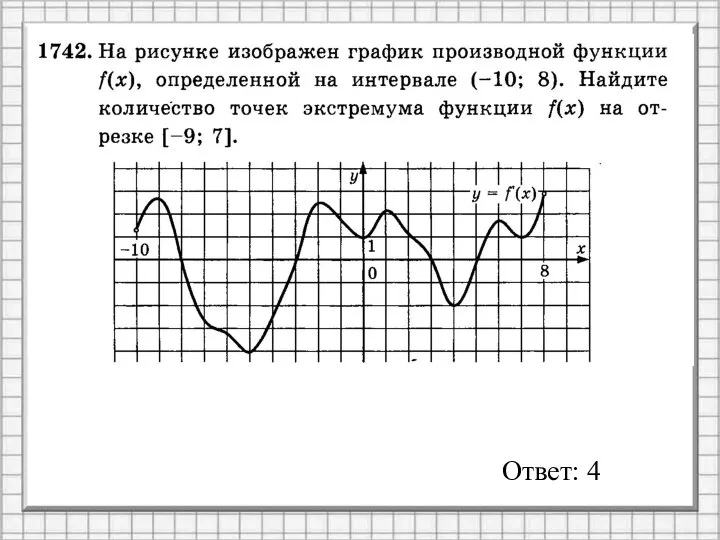
- 4. Ответ: 4
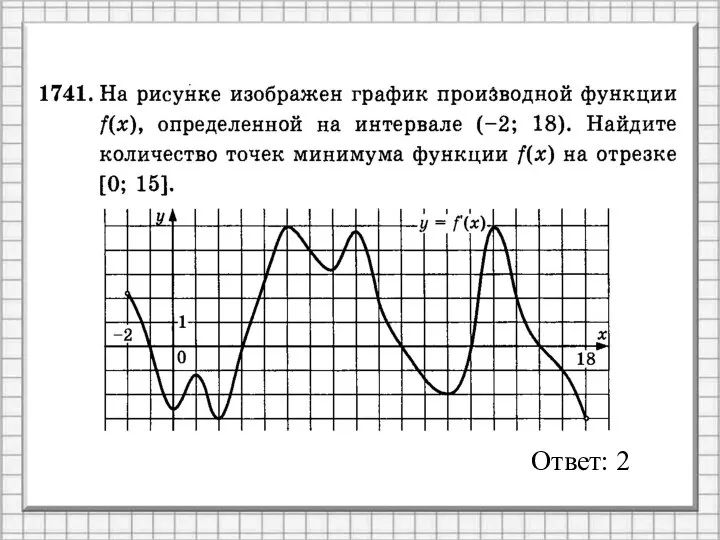
- 5. Ответ: 2
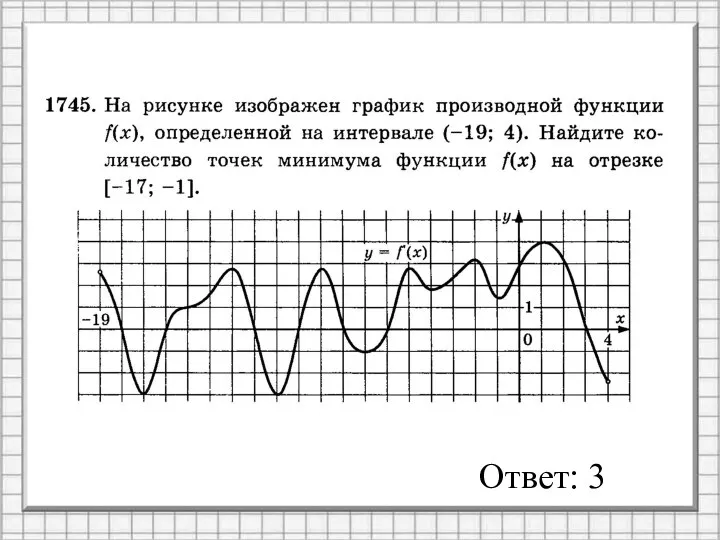
- 6. Ответ: 3
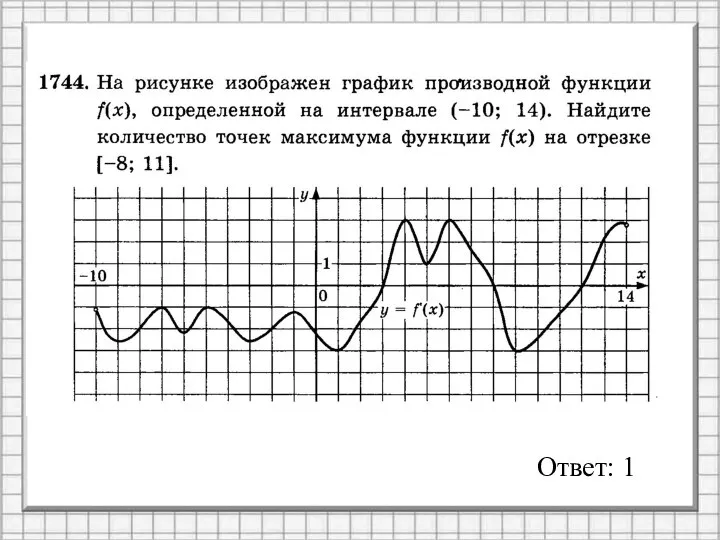
- 7. Ответ: 1
- 8. Внутреннюю точку х0 промежутка I, т. е. точку, принадлежащую интервалу (а; b), называют критической точкой функции
- 9. Пусть функция f(x) непрерывна на промежутке I вместе со своей производной f'(x). Рассмотрим случай, когда внутри
- 10. Пусть теперь на промежутке I с концами а и b функция f(х) непрерывна вместе со своей
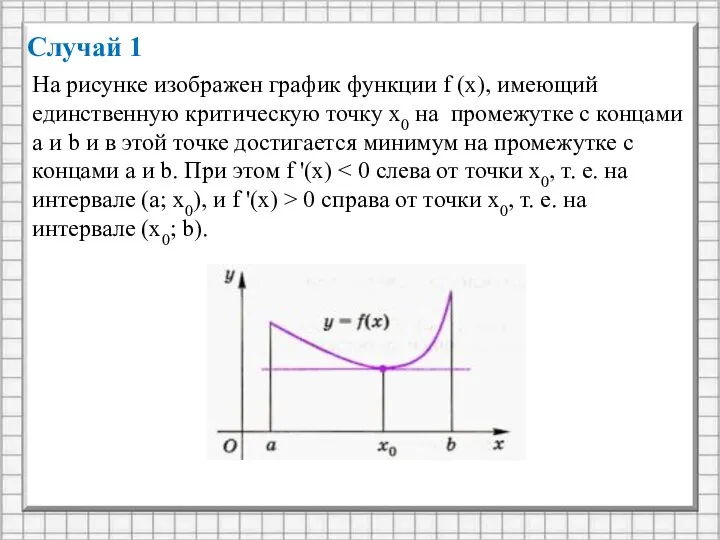
- 11. Случай 1 На рисунке изображен график функции f (x), имеющий единственную критическую точку х0 на промежутке
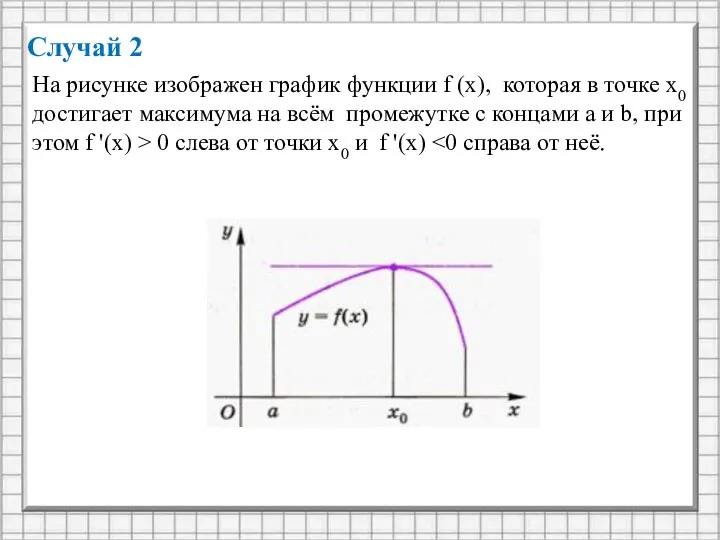
- 12. Случай 2 На рисунке изображен график функции f (x), которая в точке х0 достигает максимума на
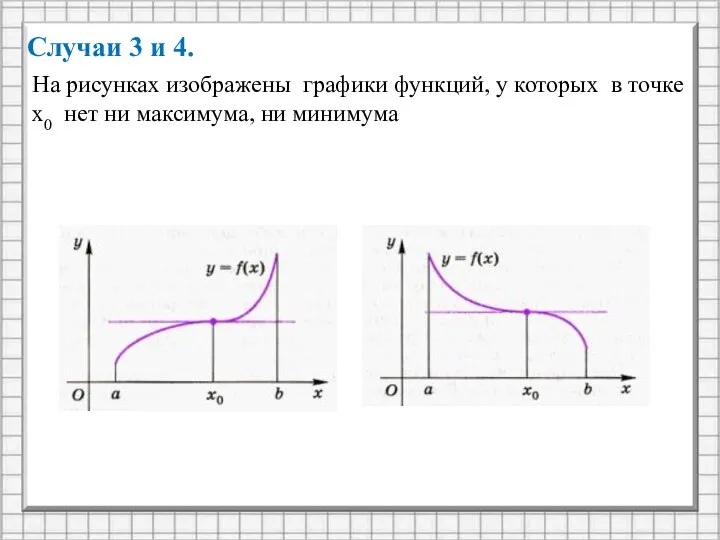
- 13. Случаи 3 и 4. На рисунках изображены графики функций, у которых в точке х0 нет ни
- 14. Утверждение 1 Пусть на промежутке I с концами а и b функция f(x) непрерывна вместе со
- 16. Утверждение 2 Пусть на промежутке I с концами а и b функция f(x) непрерывна со своей
- 19. Скачать презентацию







 Кратчайшие расстояния
Кратчайшие расстояния Рівняння
Рівняння Первообразная и неопределённый интеграл, основные свойства
Первообразная и неопределённый интеграл, основные свойства Применение производной к построению графиков функций
Применение производной к построению графиков функций Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Безопасное колесо и законы математики
Безопасное колесо и законы математики Задачи на нахождение элементов призмы
Задачи на нахождение элементов призмы Преобразование графиков функции
Преобразование графиков функции Тригонометрические уравнения
Тригонометрические уравнения Решение уравнений и неравенств
Решение уравнений и неравенств Простейшие функции и их графики
Простейшие функции и их графики Вычисление пределов функции в точке
Вычисление пределов функции в точке Свойства сторон и углов треугольника
Свойства сторон и углов треугольника Комплексные числа
Комплексные числа Подготовка к ЕГЭ 2013 год. В9. Тема: Расстояние в пространстве
Подготовка к ЕГЭ 2013 год. В9. Тема: Расстояние в пространстве Ошибки результатов измерений
Ошибки результатов измерений Площадь фигур. Решение задач по готовым чертежам
Площадь фигур. Решение задач по готовым чертежам Определение свойств функции по графику
Определение свойств функции по графику Интерактивный тренажёр Повторяем величины с домовёнком
Интерактивный тренажёр Повторяем величины с домовёнком Презентация на тему Тетраэдр
Презентация на тему Тетраэдр  Формулы приведения
Формулы приведения Логические задачи. 1 класс
Логические задачи. 1 класс Волшебная страна - Геометрия
Волшебная страна - Геометрия Проверка деления
Проверка деления Урок начинается. Занимательная математика
Урок начинается. Занимательная математика Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Презентация на тему Округление десятичных чисел
Презентация на тему Округление десятичных чисел  Применение математики в банковском деле
Применение математики в банковском деле