Содержание
- 2. Содержание лекции Определение вектора Модуль вектора Виды векторов Координаты вектора Сложение и вычитание векторов Умножение вектора
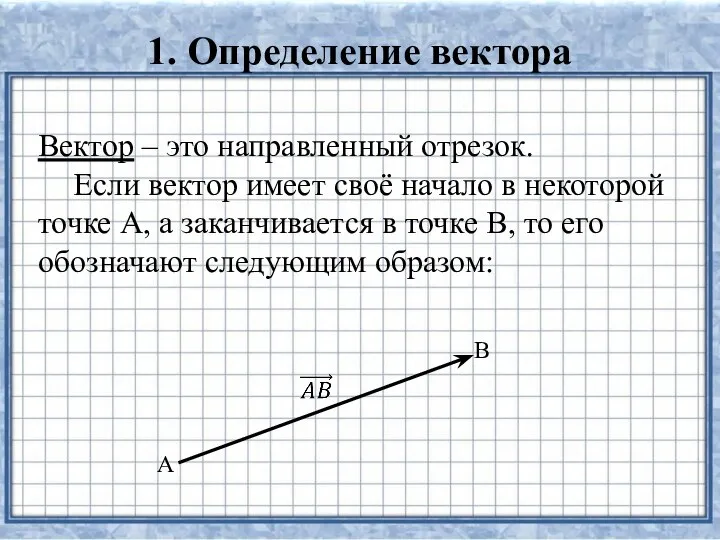
- 3. 1. Определение вектора Вектор – это направленный отрезок. Если вектор имеет своё начало в некоторой точке
- 4. 2. Модуль вектора Длиной вектора (его модулем) называют расстояние между концом вектора и его началом. Для
- 5. 3. Виды векторов Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то
- 6. Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными. Если
- 7. 4. Координаты вектора Для нахождения координаты вектора следует вычесть соответствующие координаты его конца и начала. Например,
- 8. 5. Сложение и вычитание векторов Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.
- 9. 6. Умножение вектора на число Чтобы умножить вектор на некоторое число, следует умножить каждую его координату
- 11. Скачать презентацию







 Повторение вычисления двухзначных чисел столбиком с переходом через десяток
Повторение вычисления двухзначных чисел столбиком с переходом через десяток Презентация на тему Деление (2 класс)
Презентация на тему Деление (2 класс)  Преобразование буквенных выражений. Правила математического синтаксиса
Преобразование буквенных выражений. Правила математического синтаксиса Конус
Конус Презентация на тему Площадь четырёхугольника
Презентация на тему Площадь четырёхугольника  Описанный четырехугольник
Описанный четырехугольник Лекция 5. Плоские и планарные графы
Лекция 5. Плоские и планарные графы Одночлены и их свойства
Одночлены и их свойства Квадратная матрица
Квадратная матрица Обобщение понятия о показателе степени
Обобщение понятия о показателе степени Задачи на построение (геометрия, 7 класс)
Задачи на построение (геометрия, 7 класс) Как можно заменить произведение равных сомножителей?
Как можно заменить произведение равных сомножителей? Сложение и вычитание в пределах 20. Повторение
Сложение и вычитание в пределах 20. Повторение Решение неравенства 2. Бандур Марина, 10 А
Решение неравенства 2. Бандур Марина, 10 А Икосаэдр
Икосаэдр Задание Квадрат
Задание Квадрат Дискриминантный анализ Фишера с kernel trick
Дискриминантный анализ Фишера с kernel trick Сложение вида 37+48. Урок №71
Сложение вида 37+48. Урок №71 Параллельность прямой и плоскости
Параллельность прямой и плоскости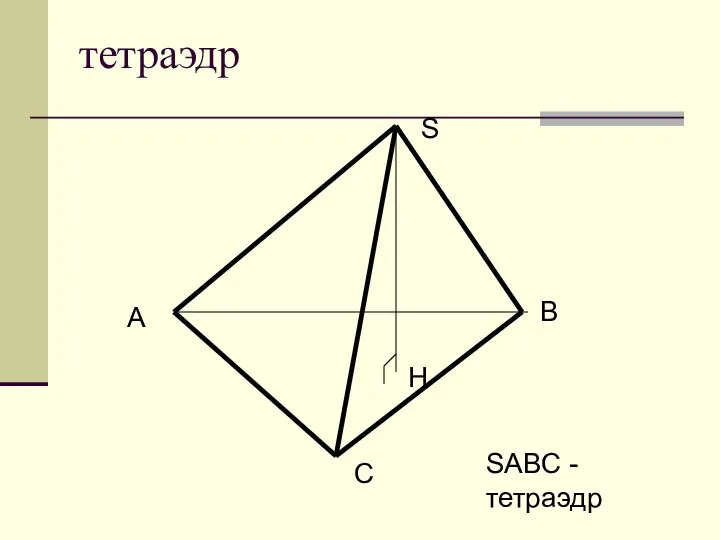 Тетраэдр
Тетраэдр Решение линейных уравнений
Решение линейных уравнений Элементы векторной алгебры
Элементы векторной алгебры Элементы комбинаторики
Элементы комбинаторики Показательные уравнения
Показательные уравнения Методы решения тригонометрических уравнений. 10 класс
Методы решения тригонометрических уравнений. 10 класс Свойства квадратных корней
Свойства квадратных корней Тема: «Нумерация. Счёт предметов. Разряды»
Тема: «Нумерация. Счёт предметов. Разряды» Случайные величины (лекция 4)
Случайные величины (лекция 4)