Слайд 2Введение
Человечество в своей деятельности постоянно создает и использует модели окружающего мира.

Развитие любой науки невозможно без создания теоретических моделей, отражающих строение, свойства и поведение реальных объектов.
Моделирование –это метод познания, состоящий из создания и исследования моделей.
Математическое моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система, находящаяся в некотором объективном соответствии с познаваемым объектом, способная замещать его в определенных отношениях и дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.
Слайд 3МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Вопрос математического моделирования можно разбить на три этапа:
Составление модели
Построение алгоритма

Создание программы
При анализе социально-исторических процессов математическое моделирование играет все более заметную роль. Имеющиеся к настоящему времени модели можно условно разделить на три группы:
Модели – концепции, основанные на выявлении и анализе общих исторических закономерностей и представлении их в виде когнитивных схем, описывающих логические связи между различными факторами, влияющими на исторические процессы.
Частные математические модели имитационного типа, посвященные описанию конкретных исторических событий
Математические модели, являющиеся промежуточными между двумя указанными типами
Слайд 4ПРИМЕР ВЗАИМОСВЯЗИ ИСТОРИЧЕСКОГО И
СТРАТЕГИЧЕСКОГО ПРОГНОЗОВ
Есть известный исторический парадокс. За много веков население

Китая и Индии выросло в десятки раз, в то время как Египта увеличилось только вдвое, и демографические циклы почему-то в Египте были гораздо короче. Убедительное объяснение этому, опирающееся на математическую модель, было дано сотрудником Института Африки РАН профессором А.В.Коротаевым.
Простейшим дифференциальным уравнением является уравнение:
y' = f(x)
Общим решением простейшего дифференциального уравнения является неопределенный интеграл:
y = f(x)dx + C
(где С – произвольная константа).
Ni+1=Ni+(r-m)Ni
Простейшее разностное уравнение можно получить в модели динамики численности популяции. разность (r – m) – коэффициент прироста. Если этот коэффициент больше нуля (рождаемость выше смертности), население растет, если меньше нуля – убывает. Эта модель роста численности населения была предложена Т. Мальтусом. Она описывала неограниченный, экспоненциальный рост человечества
Слайд 5Томас Роберт Мальтус (1766-1834) – видный представитель классической политической экономики Англии. Творчество

этого ученого формировалось в основном в первой четверти XIX в., но результаты его научных изысканий ценны и для современной экономической теории.
Слайд 6Теория Мальтуса
Теория Мальтуса состоит из трех положений:
1 Биологическая способность человека

к продолжению рода превосходит его физическую способность увеличить свои продовольственные ресурсы
2 Те или иные ограничения роста населения — принудительные или предупредительные — действуют всегда
3 Конечный предел воспроизводственной способности населения определяется ограничением по продовольственным ресурсам





 Параллельные плоскости
Параллельные плоскости Приёмы умножения на 2
Приёмы умножения на 2 Математика 4 класс
Математика 4 класс Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Математика в профессии Застройщик
Математика в профессии Застройщик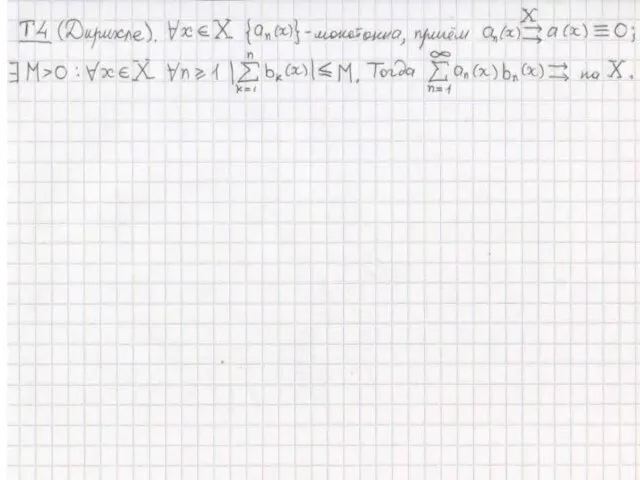 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Презентация на тему Пропорции
Презентация на тему Пропорции  Перетворення графіків
Перетворення графіків Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Обыкновенные дроби
Обыкновенные дроби Устная работа. Вычисления
Устная работа. Вычисления Вычисление реакций и перемещений в статически неопределимых системах
Вычисление реакций и перемещений в статически неопределимых системах Перпендикулярные прямые
Перпендикулярные прямые Функциональная грамотность (математика) - задачи
Функциональная грамотность (математика) - задачи Решение тригонометрических уравнений
Решение тригонометрических уравнений Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10
Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10 Сложение отрицательных чисел
Сложение отрицательных чисел Построение правильных многоугольников
Построение правильных многоугольников Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Золотое сечение. Витрувий
Золотое сечение. Витрувий Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком  Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Понятие и виды средних величин
Понятие и виды средних величин Презентация на тему Вклад Пифагора в развитие музыки 7 класс
Презентация на тему Вклад Пифагора в развитие музыки 7 класс  Квадратные неравенства с параметрами
Квадратные неравенства с параметрами Логарифм и его свойства
Логарифм и его свойства