Слайд 2
ПЛАН
1. Основные понятия.
2. Геометрическое изображение комплексных чисел.
3. Формы записи комплексных чисел.
4. Действия

над комплексными числами.
5. Зачем изучать комплексные числа?
Слайд 52. Геометрическое изображение комплексных чисел.
М
x
y

Слайд 113. Формы записи комплексных чисел.

Слайд 19Извлечение корней из комплексных чисел

Слайд 20Зачем изучать комплексные числа?
На множестве С вводятся понятия функции, предела таким образом,

что соответствующие понятия действительного анализа рассматриваются как частный случай. При этом сохраняются известные свойства функций действительного переменного: теоремы о пределах, правила дифференцирования, формулы интегрирования и т.д. Однако, благодаря расширению класса функций появляются новые свойства. Например, доказывается, что из существования производной функции следует существование её производных n-го порядка в области. Устанавливается, что все элементарные функции связаны между собой: тригонометрические функции выражаются через показательную функцию, а обратные тригонометрические функции – через логарифмическую. Значительно глубже, чем в анализе функций действительного переменного, развита геометрическая теория – конформные отображения. Благодаря сочетанию аналитических и геометрических методов теория функций комплексного переменного находит широкое применение в других разделах математики и прикладных задач.
Слайд 21 Одним из важных приложений ТФКП является операционное исчисление, которое применяется для решения

обыкновенных дифференциальных уравнений и разностных уравнений с постоянными коэффициентами.























 Математика в химии или химия в математике?
Математика в химии или химия в математике? Прямоугольник, его свойства и признаки
Прямоугольник, его свойства и признаки Элективный курс. Алгебра 11 класс. Урок 06
Элективный курс. Алгебра 11 класс. Урок 06 Задачи на проценты
Задачи на проценты Задания для домашнего обучения
Задания для домашнего обучения Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур Системы счисления
Системы счисления Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Решение квадратных неравенств
Решение квадратных неравенств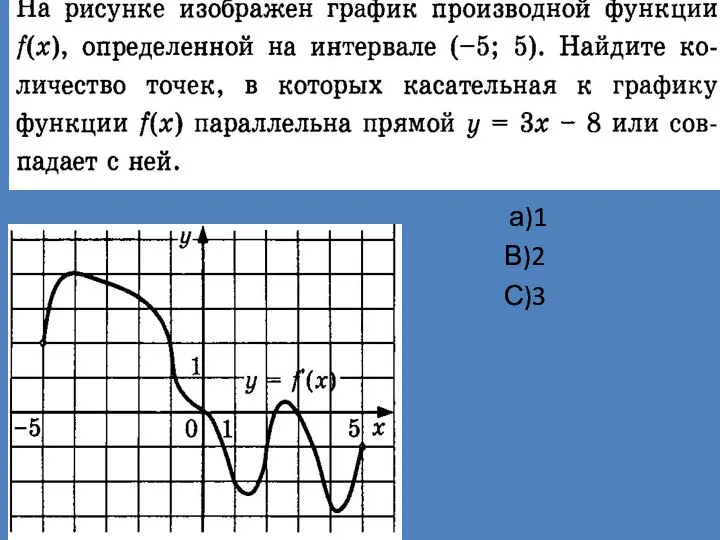 График производной функции
График производной функции Практикум №5. Сквозной пример
Практикум №5. Сквозной пример Литр. Задачи
Литр. Задачи Сколько раз в день минутная и часовая стрелки образуют прямую линию?
Сколько раз в день минутная и часовая стрелки образуют прямую линию? Теория вероятностей
Теория вероятностей Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком  Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8
Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8 Многогранники. Задания
Многогранники. Задания Квадратные корни. Обобщающий урок
Квадратные корни. Обобщающий урок Элементы комбинаторики
Элементы комбинаторики Решение комбинаторных задач
Решение комбинаторных задач Умножение натуральных чисел 5 класс
Умножение натуральных чисел 5 класс ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ»
ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ» Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Показательные уравнения
Показательные уравнения Решение показательных уравнений. Корень уравнения
Решение показательных уравнений. Корень уравнения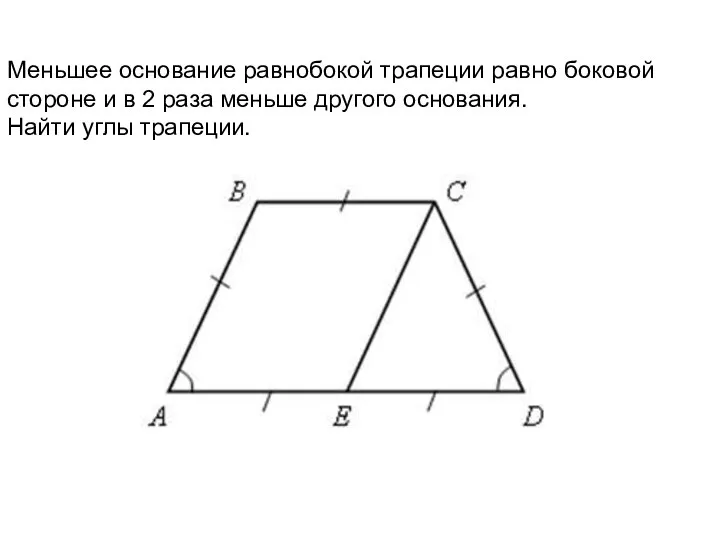 Параллелограмм и трапеция. Урок 8
Параллелограмм и трапеция. Урок 8 Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел
Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел  Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1)