Пирамида – это многогранник, составленный из n-угольника

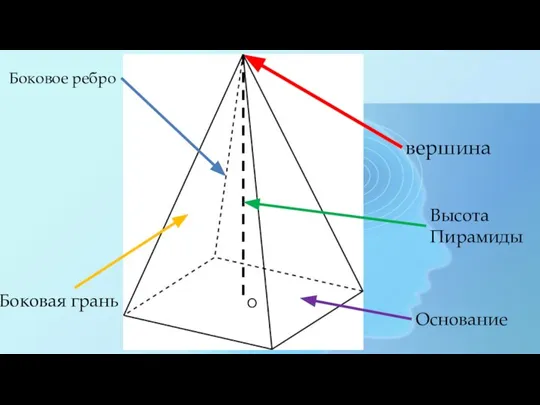
вершина
О
Высота
Пирамиды
Боковое ребро
Боковая грань
Основание

СВОЙСТВА
1) Около основания пирамиды можно описать окружность, если боковые ребра имеют одинаковую длину, при этом вершина пирамиды будет проецироваться в центр этой окружности. Боковые ребра образуют с плоскостью основания одинаковые углы
2) Если боковые грани одинаково наклонены к плоскости основания, то около основания пирамиды можно описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности, а также высоты боковых граней имеют равную длину.

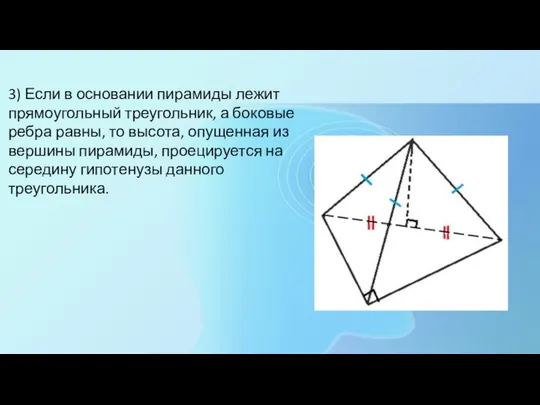
3) Если в основании пирамиды лежит прямоугольный треугольник, а боковые ребра равны, то высота, опущенная из вершины пирамиды, проецируется на середину гипотенузы данного треугольника.

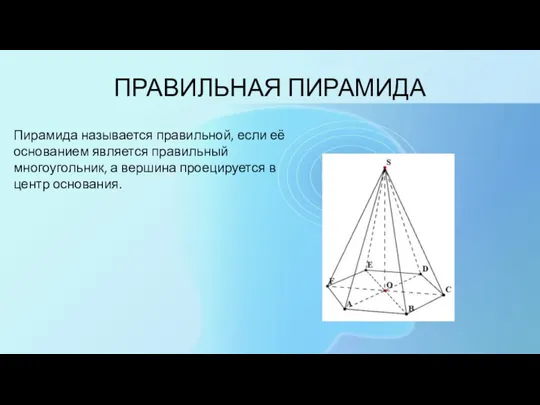
ПРАВИЛЬНАЯ ПИРАМИДА
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.

ПЛОЩАДЬ ПИРАМИДЫ

Площадь боковой поверхности равняется половине произведения периметра основания на высоту боковой грани (?)
S = 0,5Phа