Содержание
- 2. Целое уравнение и его корни 1. Повторение. Схемы решения простейших уравнений. 2. Определение понятия целого уравнения.
- 3. Повторение: Линейные уравнения
- 5. Решите уравнения: 5 + х = 7 5 + х = 5 х + 3 =
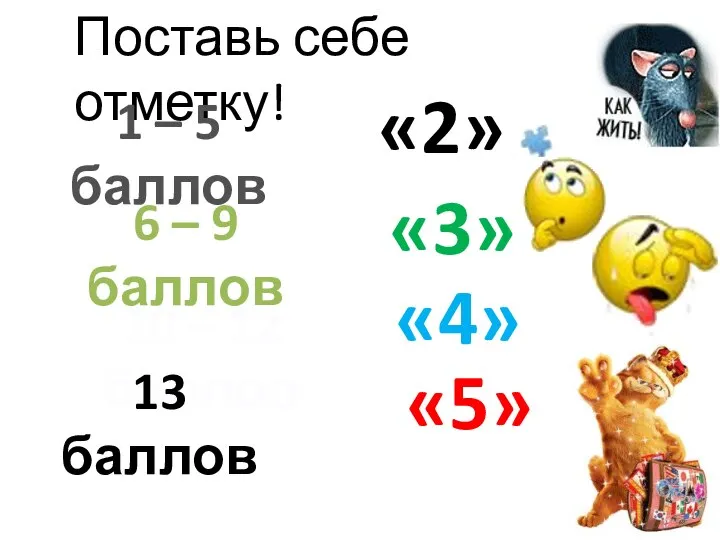
- 6. Поставь себе отметку! 1 – 5 баллов 6 – 9 баллов 10 – 12 баллов 13
- 7. Целое уравнение и его корни Уравнения, в которых левая и правая части являются целыми выражениями, называются
- 8. Какова степень уравнения: А) Б) В) Г) 5 6 5 2
- 9. Какова степень уравнения: Д) Е) 1 1
- 10. Что необходимо знать при решении уравнений? Формулы сокращённого умножения: Раскрытие скобок:
- 11. Что необходимо знать при решении уравнений? 3. Раскрытие скобок: 4. Приведение подобных слагаемых. (Подобные слагаемые- слагаемые,
- 12. ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ЦЕЛЫХ УРАВНЕНИЙ 1. Метод разложения на множители Разложить на множители можно с помощью
- 13. вынесения общего множителя за скобки способом группировки Пример. Разложить на множители можно с помощью
- 14. разложения квадратного трёхчлена на множители - корни квадратного трёхчлена Разложить на множители можно с помощью
- 15. 2. Метод введения новой переменной Схема. Сделать замену. Решить уравнение в новых переменных. 3. Вернуться к
- 16. Пример. Введём замену: Тогда в новых переменных уравнение принимает вид: Вернёмся к замене: 1) 2) Ответ:
- 17. Биквадратное уравнение: Решение методом введения новой переменной: Получим квадратное уравнение: -корни квадратного уравнения Вернёмся к замене:
- 19. Скачать презентацию


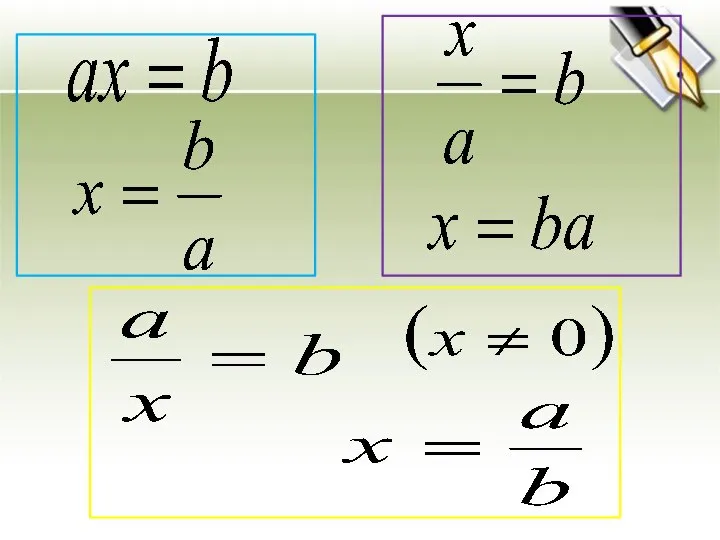
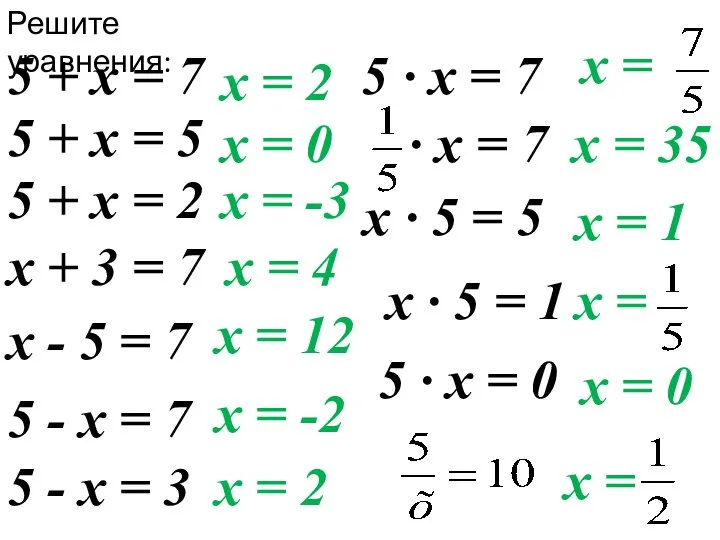











 Четырехугольники. Свойства четырехугольников. Решение задач
Четырехугольники. Свойства четырехугольников. Решение задач Взаимное расположение прямых в пространстве. Угол между прямыми
Взаимное расположение прямых в пространстве. Угол между прямыми Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Мысли о ЕГЭ
Мысли о ЕГЭ Презентация на тему Космическое путешествие 1 класс
Презентация на тему Космическое путешествие 1 класс  Конус. Решение задач по готовым чертежам
Конус. Решение задач по готовым чертежам Математические методы в экономике. Лекция 8
Математические методы в экономике. Лекция 8 Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Формулы сокращенного умножения. Разность квадратов
Формулы сокращенного умножения. Разность квадратов Деление на 2
Деление на 2 Презентация на тему Решение задач В ЕГЭ по теории вероятности
Презентация на тему Решение задач В ЕГЭ по теории вероятности  Способы быстрого счета
Способы быстрого счета Parallogramm
Parallogramm Вероятность равновозможных событий
Вероятность равновозможных событий Координаты середины отрезка. Задачи
Координаты середины отрезка. Задачи Игра 3
Игра 3 Физико-математические основы ОФЭКТ
Физико-математические основы ОФЭКТ Формулы приведения. Математический диктант
Формулы приведения. Математический диктант Правильные многогранники
Правильные многогранники Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс Решение текстовых задач
Решение текстовых задач Последовательность процентных расчетов при осуществлении банковских операций
Последовательность процентных расчетов при осуществлении банковских операций Теория графов
Теория графов Степенная функция
Степенная функция Презентация на тему Площадь круга
Презентация на тему Площадь круга  Пропорциональные отрезки в прямоугольном треугольнике (8 класс)
Пропорциональные отрезки в прямоугольном треугольнике (8 класс) Разложение многочлена на множители
Разложение многочлена на множители Презентация на тему ЗАДАЧИ НА ДРОБИ
Презентация на тему ЗАДАЧИ НА ДРОБИ