Содержание
- 2. Куб (или гексаэдр) (греч. εξάεδρο – Шестигранник) составлен из шести квадратов. Каждая вершина куба является вершиной
- 3. Форму куба имеет монокристалл поваренной соли, Поваренная соль (NaCl) — пищевой продукт. Производится и используется после
- 4. Куб в архитектуре. В Роттердаме — архитектор наклонил обычный дом на 45 градусов так, что три
- 5. «Кубик Рубика» (разговорный вариант Кубик-рубик; первоначально был известен как «Магический кубик») — механическая головоломка, изобретённая в
- 6. Моделирование многогранников: А также! Модели куба можно изготовить, используя технику оригами!
- 7. Модели куба можно изготовить из разверток, используя конструктор!
- 8. Чертеж куба: Невидимые грани куба изображаем на чертеже- пунктиром.
- 9. 1. У куба 10 вершин? Ответьте на следующие вопросы, используя Ваш куб: Вершин - 2. Сколько
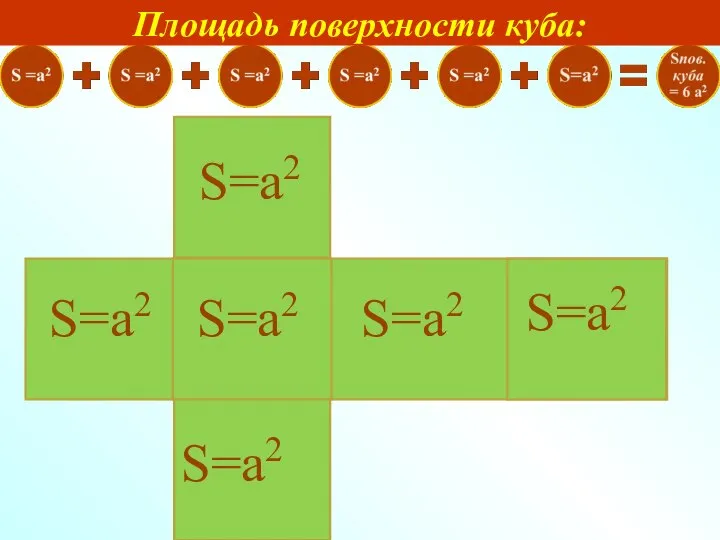
- 10. Измерения куба Площадь поверхности куба равна сумме площадей шести его граней или произведению площади одной грани
- 11. S=а2 S=а2 S=а2 S=а2 S=а2 S=а2 Площадь поверхности куба:
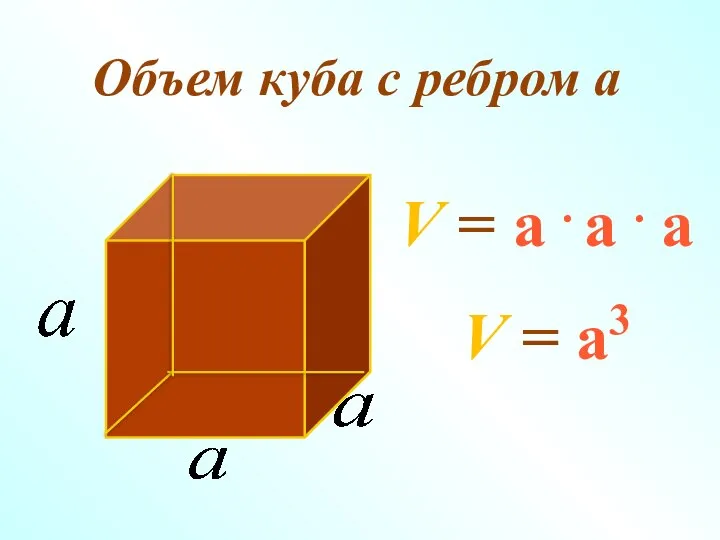
- 12. V = a . а . а V = a3 Объем куба с ребром а
- 14. Скачать презентацию









 Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции
Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции Математическая статистика
Математическая статистика Угол. Виды углов
Угол. Виды углов Вторая теорема о среднем. Формула Бонне
Вторая теорема о среднем. Формула Бонне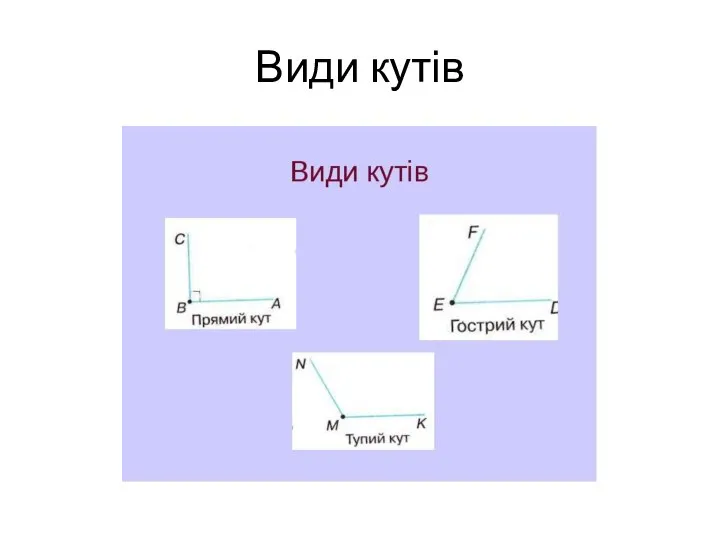 Види кутів
Види кутів Формирование элементарных математических представлений
Формирование элементарных математических представлений Квадратичная функция, ее график. Преобразование графика квадратичной функции
Квадратичная функция, ее график. Преобразование графика квадратичной функции Презентация на тему Использование графов в решении логических задач
Презентация на тему Использование графов в решении логических задач  Работа над ошибками СОР. Подготовка к СОЧ
Работа над ошибками СОР. Подготовка к СОЧ Переместительный закон умножения
Переместительный закон умножения На лесной поляне
На лесной поляне Среднее арифметическое. Задания
Среднее арифметическое. Задания Интеграл и его приложения
Интеграл и его приложения ТАиФЯ № 1 (Введение)
ТАиФЯ № 1 (Введение) Знакомство с деятельностью Ивана Грозного, через решение математических задач
Знакомство с деятельностью Ивана Грозного, через решение математических задач Десятки, единицы, цифры
Десятки, единицы, цифры Числа второго десятка
Числа второго десятка Теорема Пифагора
Теорема Пифагора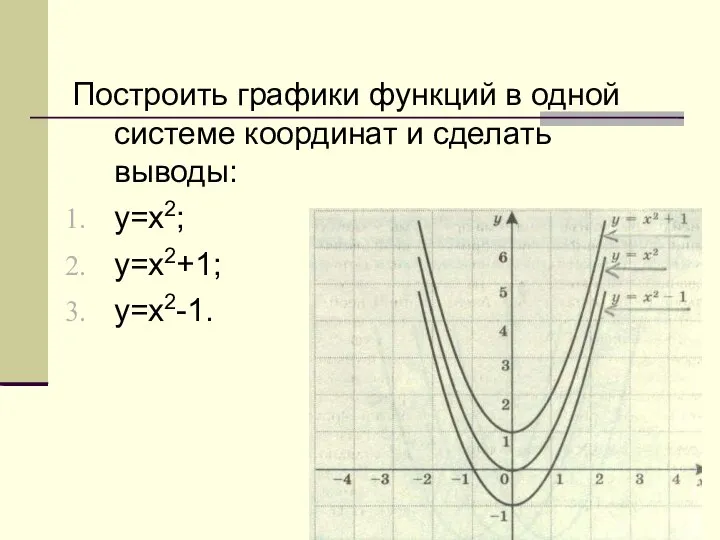 Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика Основные понятия за 100
Основные понятия за 100 Презентация на тему Статистика
Презентация на тему Статистика  Сокращение дробей. 6 класс
Сокращение дробей. 6 класс Презентация на тему Линейная функция и ее график (7 класс)
Презентация на тему Линейная функция и ее график (7 класс)  Математическое моделирование, внедрение методов численного анализа в системах. Расчетный эксперимент
Математическое моделирование, внедрение методов численного анализа в системах. Расчетный эксперимент свойства функции
свойства функции Симметрия относительно прямой
Симметрия относительно прямой Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Вычисление логарифмов
Вычисление логарифмов