Содержание
- 2. Комбинаторикой называют область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или
- 3. Число перестановок. Определение: Отличающиеся друг от друга порядком наборы, составленные из всех элементов данного конечного множества,
- 4. Пример 2. Цифры 1, 2, 3, 4 написаны на четырех карточках. Сколько различных четырехзначных чисел можно
- 5. Число размещений. Определение: Упорядоченные наборы, состоящие из к различных элементов, выбранных из данных n элементов, называются
- 6. Пример 5. Студентам надо сдать 4 экзамена за 8 дней. Сколькими способами можно составить расписание сдачи
- 7. Число сочетаний. Определение: Неупорядоченные наборы, состоящие из к элементов, взятых из данных n элементов, называются сочетаниями
- 8. Пример 7. В спортивном турнире участвует 6 команд. Каждая команда должна сыграть с каждой одну игру.
- 9. Пример 8. Из трех групп студентов необходимо составить команду, содержащую по одному человеку из каждой группы.
- 10. Пример 10. Какое количество различных символов (букв, чисел и т.д.) можно передать не более чем пятью
- 11. НЬЮТОНА БИНОМ разложение алгебраической суммы двух слагаемых произвольной степени. Впервые была предложена Ньютоном в 1664–1665: Коэффициенты
- 13. Скачать презентацию










 Математика. Решение задач
Математика. Решение задач Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ Решение неравенств. ЕГЭ, задание 15
Решение неравенств. ЕГЭ, задание 15 Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Умножение десятичных дробей
Умножение десятичных дробей Применение преобразований графиков функций
Применение преобразований графиков функций Первообразная функции
Первообразная функции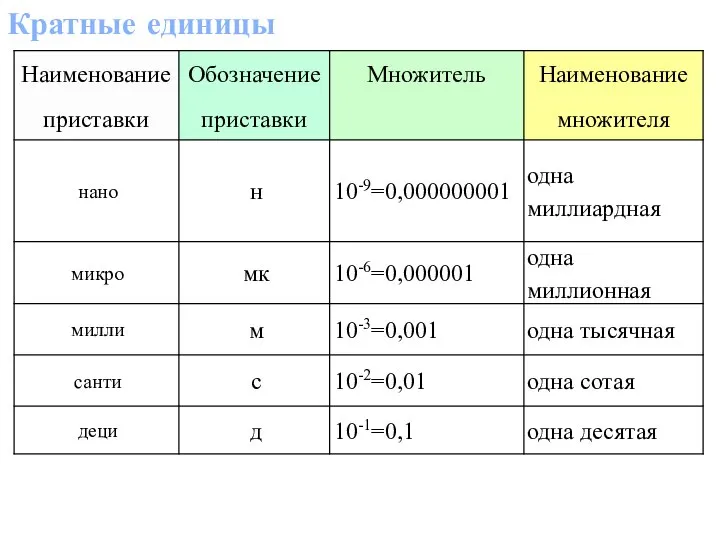 Кратные единицы
Кратные единицы Математические иллюзии
Математические иллюзии Параллельные прямые
Параллельные прямые Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Методы решения творческих задач
Методы решения творческих задач Обыкновенные дроби. Основное свойство дроби. 5 класс
Обыкновенные дроби. Основное свойство дроби. 5 класс Точки экстремума. Промежутки возрастания и убывания функции
Точки экстремума. Промежутки возрастания и убывания функции координаты вектора
координаты вектора Основное тригонометрическое тождество и его следствия
Основное тригонометрическое тождество и его следствия Древнекитайское доказательство
Древнекитайское доказательство Задачи на проценты
Задачи на проценты Математика. Роль математики в жизни людей и общества
Математика. Роль математики в жизни людей и общества Программа по математике для начальной школы в соответствии с ФГОС - 2
Программа по математике для начальной школы в соответствии с ФГОС - 2 Презентация на тему Двугранный угол (10 класс)
Презентация на тему Двугранный угол (10 класс)  Геометрическое место точек. 7 класс
Геометрическое место точек. 7 класс Проценты. Графический диктант
Проценты. Графический диктант Метрология: применение математической статистики при измерениях и испытаниях
Метрология: применение математической статистики при измерениях и испытаниях Сложение и вычитание трёхзначных чисел. Геометрическое задание
Сложение и вычитание трёхзначных чисел. Геометрическое задание Проценты
Проценты Погрешность прямых измерений
Погрешность прямых измерений Классификация функций
Классификация функций