Содержание
- 2. Вспомним какие бывают числа (: Link: https://ru.wikipedia.org/wiki/Число
- 3. Что для нас важно? Главным образом в криптографии используются НАТУРАЛЬНЫЕ числа. Мы не работаем с дробными,
- 4. Что еще для нас важно? В криптографии как правило используется не бесконечное множество натуральных чисел, а
- 5. Алгебраические свойства
- 7. Какие алгебраические свойства у операции бывают? 1) Конечно же + (известно со школы – от перестановки
- 8. Ок, это было просто, а какие тогда не коммутативны? 2) Матрицы, матрицы... Ага. Перемножение матриц!
- 9. Какие они бывают?
- 10. Вроде разобрались. У нас есть некоторые операции и свойства этих операций. А еще мы будем работать
- 11. Алгебраические структуры
- 12. К основным алгебраическим структурам относятся: Алгебраические структуры с одной бинарной операцией Группоид Полугруппа Моноид Группа Алгебраические
- 15. Так так так стоп! Ничего не понятно, что за нейтральный элемент, что за обратный элемент и
- 16. Нейтральный элемент Ничего сложного, правда? Да и вы и сами сможете назвать нейтральный элемент множества натуральных
- 17. Обратный элемент Что будет обратным элементов для 4 по умножению для множества рациональных чисел (те, что
- 20. Поле Группа с четырьмя операциями, имеющие свойства, близкие к свойствам четырех основных операций с числами (сложения,
- 21. Математические операции 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
- 22. Функция Эйлера
- 24. Скачать презентацию





















 Теорема Пифагора
Теорема Пифагора Классы интегрируемых функций
Классы интегрируемых функций Интеллектуальная игра по математике для 8 класса
Интеллектуальная игра по математике для 8 класса Движение в геометрии
Движение в геометрии Математическая модель
Математическая модель Примеры. Карточки, счет +-10, 11, 12
Примеры. Карточки, счет +-10, 11, 12 Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Масса предметов
Масса предметов Теория игр
Теория игр Методика изучения площади
Методика изучения площади Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Осевая семетрия
Осевая семетрия Координатная плоскость. Ордината. Абсцисса
Координатная плоскость. Ордината. Абсцисса Алгоритм и письменное деление на двузначное число
Алгоритм и письменное деление на двузначное число Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)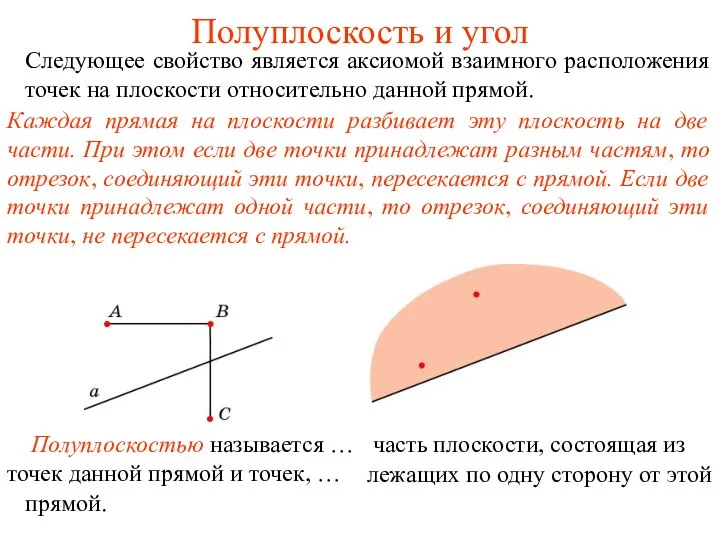 Полуплоскость и угол
Полуплоскость и угол Компланарны ли тройки векторов
Компланарны ли тройки векторов Четырехугольники
Четырехугольники Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Математика интелектуальная разминка
Математика интелектуальная разминка Усеченый конус
Усеченый конус Кратчайшие расстояния
Кратчайшие расстояния Параллельные прямые 7 класс
Параллельные прямые 7 класс Таблица истинности
Таблица истинности Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед
Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед Таблицы данных с двумя переменными
Таблицы данных с двумя переменными Показательные уравнения и неравенства
Показательные уравнения и неравенства