Содержание
- 2. Задачи интеллектуального анализа данных Задачи ИАД Описательные Ассоциативные правила Кластеризация Классификация Прогнозирование Предсказательные
- 3. Введение Задача кластеризации состоит в разделении исследуемого множества объектов на группы «похожих» объектов, называемых кластерами Решение
- 4. Кластеризация отличается от классификации тем, что этап обучения на примерах отсутствует В задачах классификации множество классов
- 5. Задача кластеризации часто решается на начальных этапах исследования, когда о данных мало что известно Ее решение
- 6. ПРИМЕР –кластеризация результатов поиска
- 8. Формальная постановка задачи Дано множество данных, состоящее из N объектов (векторов): S1, S2, …, SN Каждый
- 9. Формальная постановка задачи Таким образом, i-й объект можно записать в виде: Si = (xi1, xi2, …,
- 10. Формальная постановка задачи Требуется: найти способ сравнения d(Sp, Sq) объектов между собой (меру сходства, функцию расстояния)
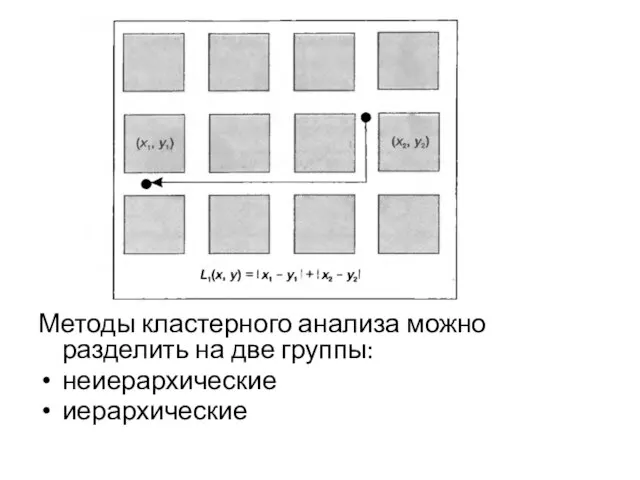
- 11. евклидово расстояние Манхэттенское расстояние расстояние Чебышева Метрики расстояния между объектами
- 12. Методы кластерного анализа можно разделить на две группы: неиерархические иерархические
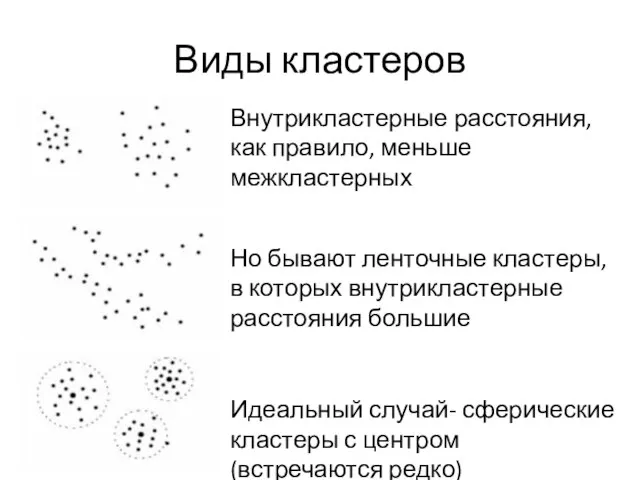
- 13. Виды кластеров Внутрикластерные расстояния, как правило, меньше межкластерных Но бывают ленточные кластеры, в которых внутрикластерные расстояния
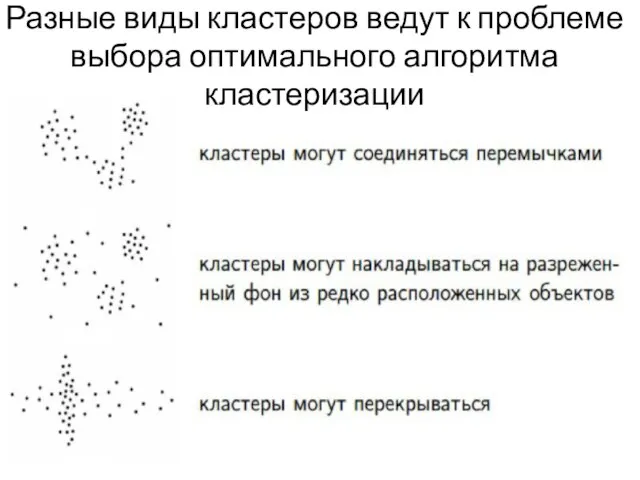
- 14. Разные виды кластеров ведут к проблеме выбора оптимального алгоритма кластеризации
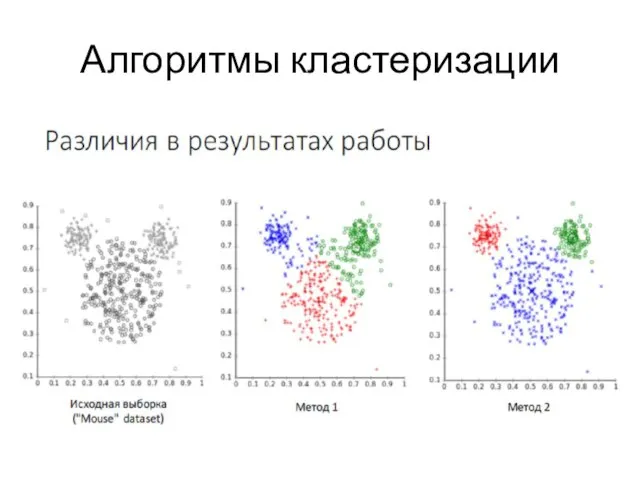
- 15. Алгоритмы кластеризации
- 16. Как сделать признаки равноправными в образовании кластеров? ИТОГ: мы получим значения признаков, 95% которых находится в
- 17. Метод k-средних Неиерархическим методом кластеризации является метод k-средних (k-means) Предварительно необходимо выбрать вероятное число кластеров k
- 18. Метод k-средних 1. Выбирается k произвольных исходных центров кластеров – обычно выбираются k объектов 2. Все
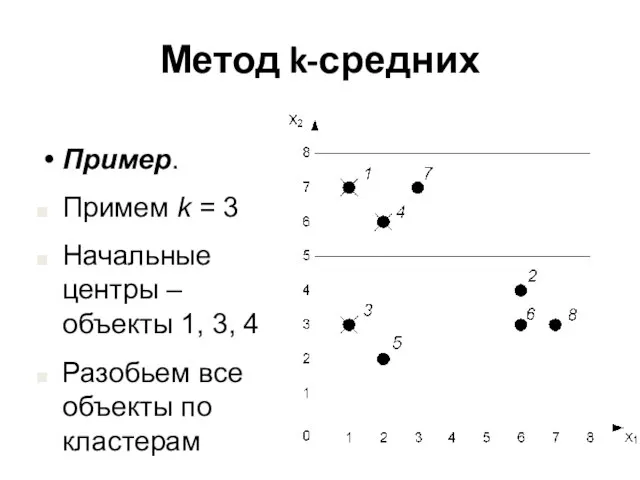
- 19. Метод k-средних Пример. Примем k = 3 Начальные центры – объекты 1, 3, 4 Разобьем все
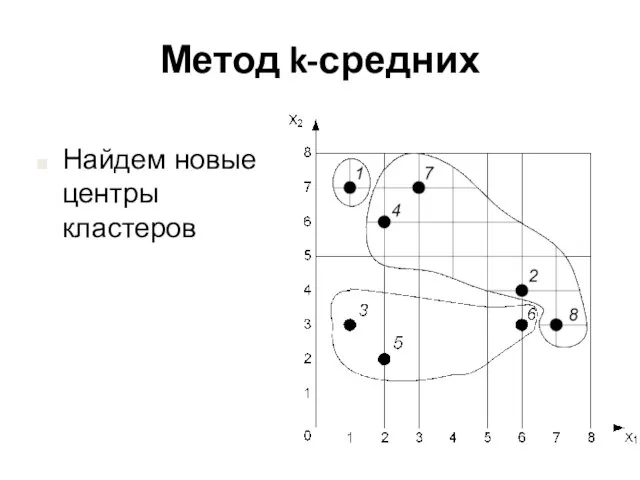
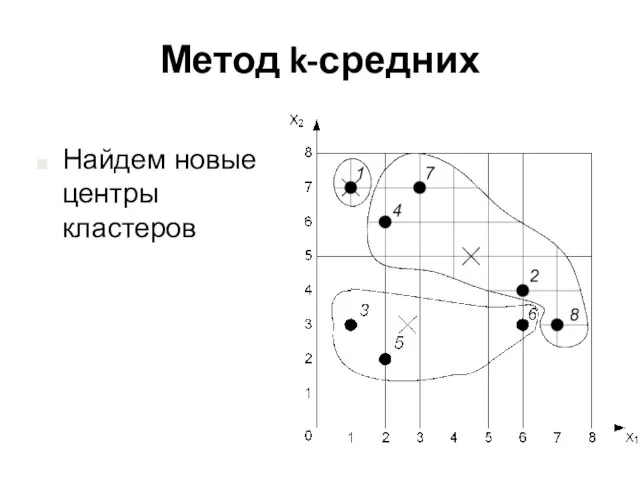
- 20. Метод k-средних Найдем новые центры кластеров
- 21. Метод k-средних Найдем новые центры кластеров
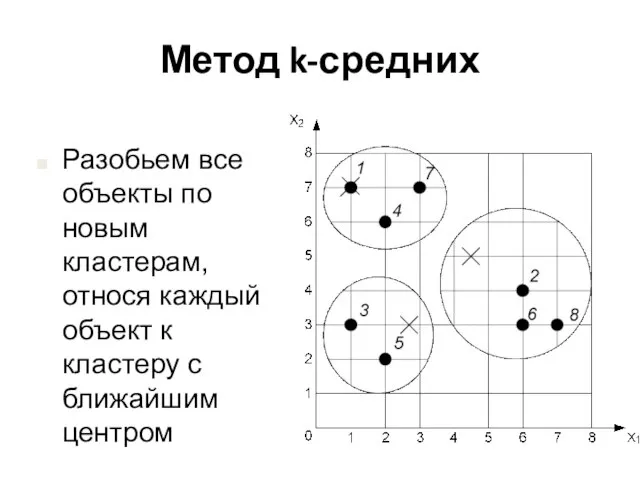
- 22. Метод k-средних Разобьем все объекты по новым кластерам, относя каждый объект к кластеру с ближайшим центром
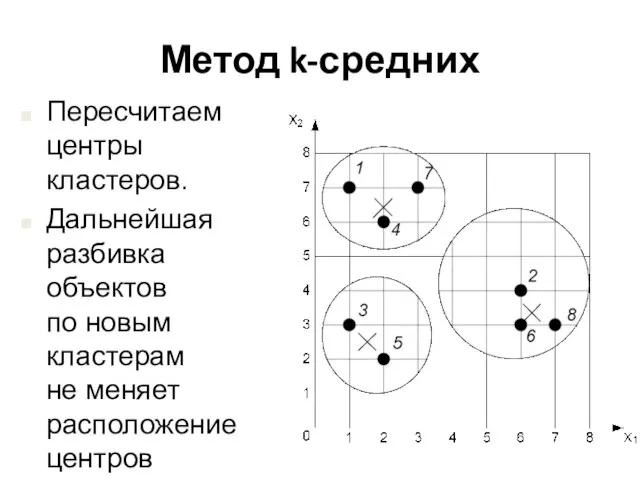
- 23. Метод k-средних Пересчитаем центры кластеров. Дальнейшая разбивка объектов по новым кластерам не меняет расположение центров
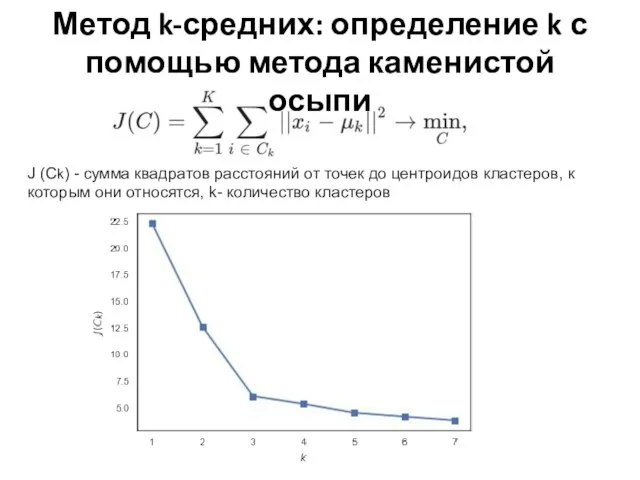
- 24. Метод k-средних: определение k с помощью метода каменистой осыпи J (Ck) - сумма квадратов расстояний от
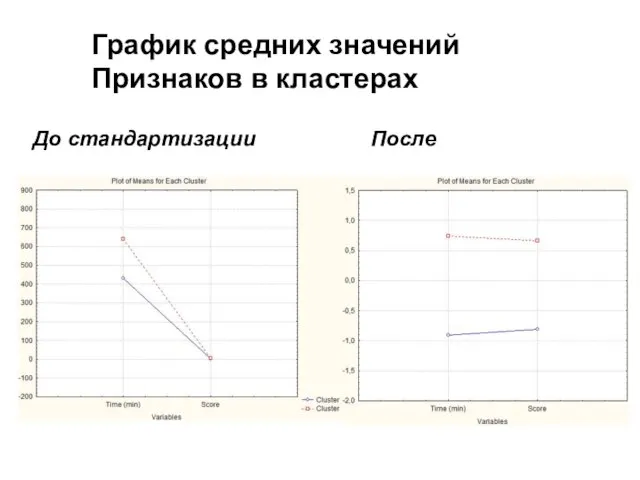
- 25. До стандартизации После График средних значений Признаков в кластерах
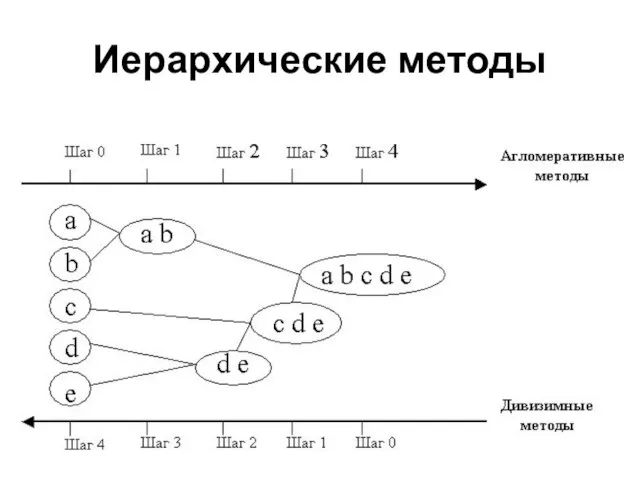
- 26. Иерархические методы К иерархическим методам кластеризации относятся: агломеративный алгоритмы дивизимный алгоритмы
- 27. Агломеративный метод В начале работы алгоритма все объекты являются отдельными кластерами На первом шаге наиболее похожие
- 28. Метод ближайшего соседа (одиночная связь, Single linkage). Расстояние между двумя кластерами определяется расстоянием между двумя наиболее
- 29. 4. Невзвешенный центроидный метод (Unweighted pair-group centroid). В этом методе расстояние между двумя кластерами определяется как
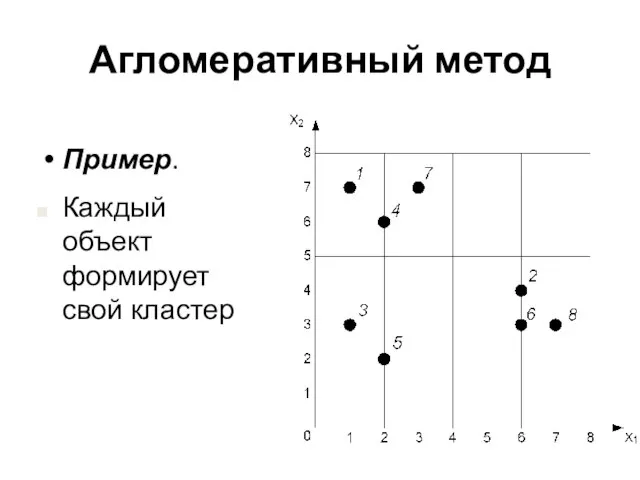
- 30. Агломеративный метод Пример. Каждый объект формирует свой кластер
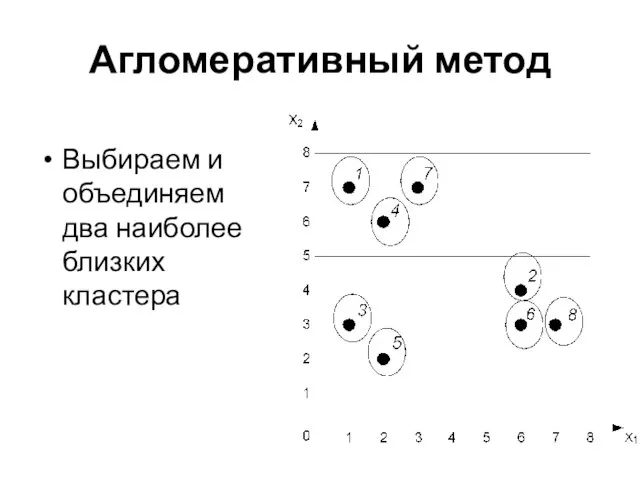
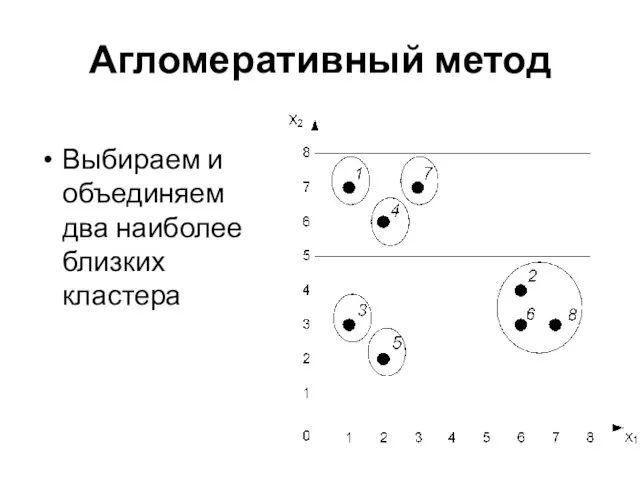
- 31. Агломеративный метод Выбираем и объединяем два наиболее близких кластера
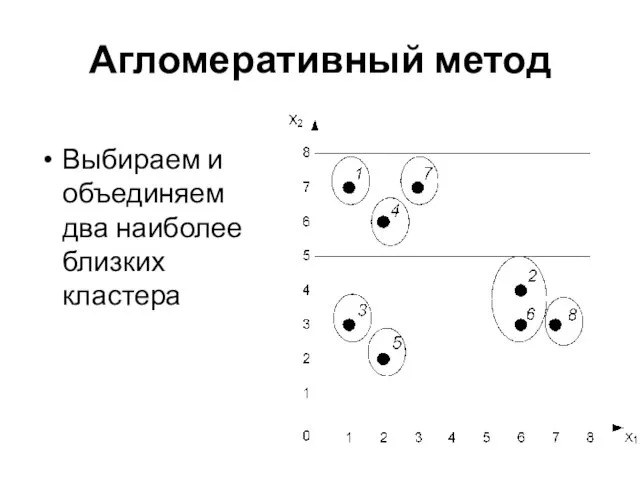
- 32. Агломеративный метод Выбираем и объединяем два наиболее близких кластера
- 33. Агломеративный метод Выбираем и объединяем два наиболее близких кластера
- 34. Дивизимный метод На первом шаге все объекты помещаются в один кластер С1 Выбирается объект, у которого
- 35. Дивизимный метод Выбранный объект удаляется из кластера С1 и формирует первый элемент второго кластера С2 На
- 36. Дивизимный метод В результате один кластер делится на два дочерних, один из которых расщепляется на следующем
- 37. Иерархические методы
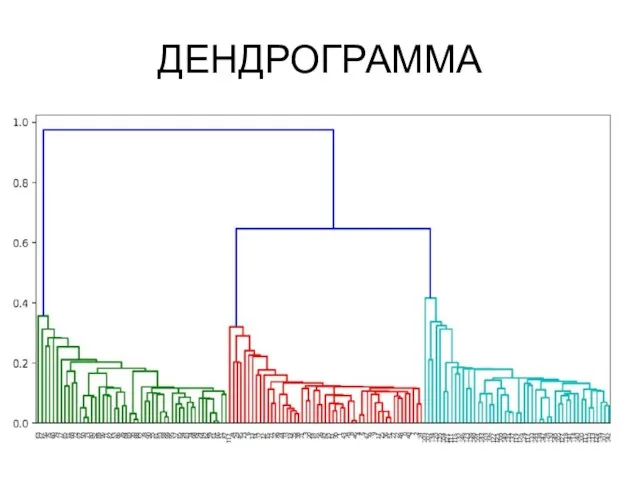
- 38. ДЕНДРОГРАММА
- 39. Метрики качества кластеризации Коэффициент силуэта: Здесь a — среднее внутрикластерное расстояние (то есть среднее расстояние между
- 40. Пример программы на Python from sklearn import datasets dataset = datasets.load_iris() X = dataset.data y =
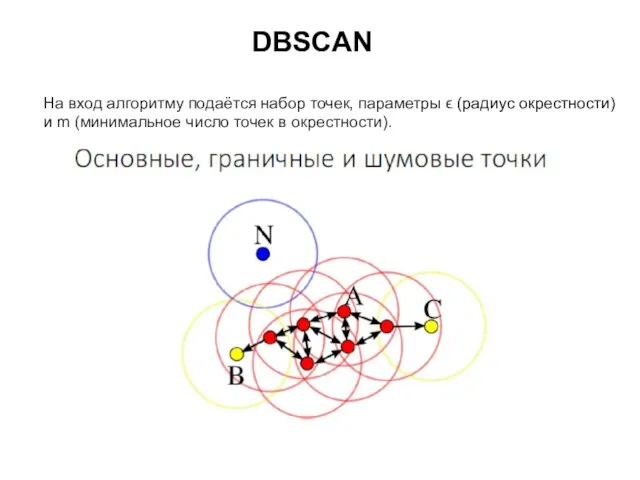
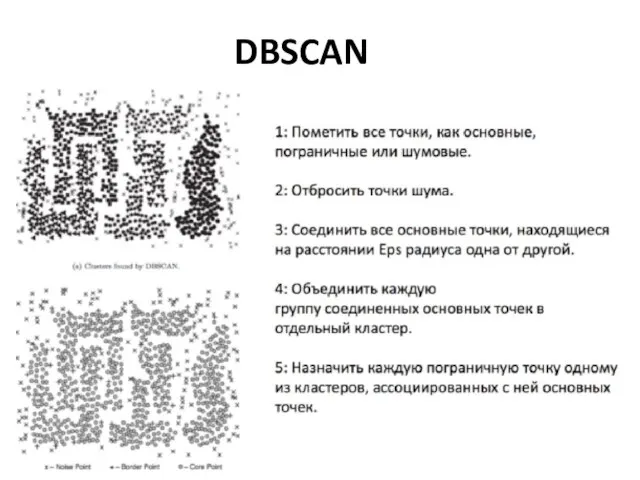
- 41. DBSCAN На вход алгоритму подаётся набор точек, параметры ϵ (радиус окрестности) и m (минимальное число точек
- 42. DBSCAN
- 43. DBSCAN: результаты работы
- 45. Скачать презентацию









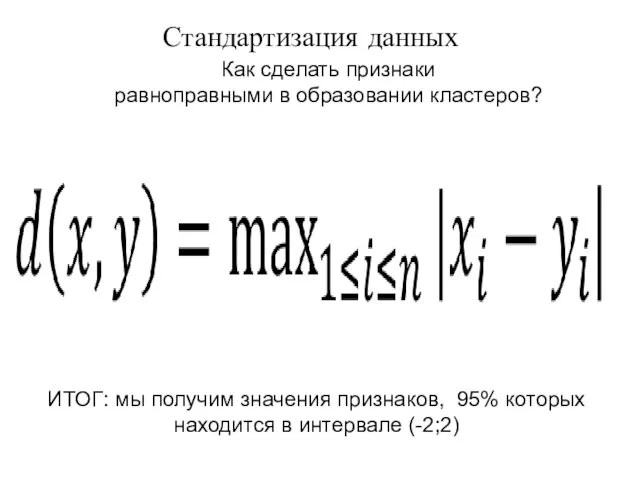












 Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Квадратний тричлен
Квадратний тричлен Перпендикуляр. Определение
Перпендикуляр. Определение Веселая математика
Веселая математика Презентация на тему Десятичные дроби и действия над ними
Презентация на тему Десятичные дроби и действия над ними  Логика, делимость. Задание №15
Логика, делимость. Задание №15 Площадь эллипса и окружности
Площадь эллипса и окружности Множество значений тригонометрических функций
Множество значений тригонометрических функций Устный счет
Устный счет Моделирование в технике
Моделирование в технике Прямоугольные треугольники
Прямоугольные треугольники Пропорции. Задачи
Пропорции. Задачи Выдающиеся российские математики. Урок-лекция, 5- 11 кл
Выдающиеся российские математики. Урок-лекция, 5- 11 кл Презентация на тему Логарифмическая функция
Презентация на тему Логарифмическая функция  Теорема Пифагора
Теорема Пифагора Неравенства. Тест
Неравенства. Тест тригонометрические неравенства (1)
тригонометрические неравенства (1) Уменьшаемое. Вычитаемое. Разность
Уменьшаемое. Вычитаемое. Разность Математика в лицах. Леонардо Пизанский (Фибоначчи)
Математика в лицах. Леонардо Пизанский (Фибоначчи) Иррациональные неравенства. Неравенства с модулем
Иррациональные неравенства. Неравенства с модулем Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости
Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости Действия над матрицами. Вычисление определителей второго и третьего порядков
Действия над матрицами. Вычисление определителей второго и третьего порядков Занимательная математика. Задачи в стихах (1 класс)
Занимательная математика. Задачи в стихах (1 класс) Элементы теории обобщенных функций
Элементы теории обобщенных функций Графический метод решения систем уравнений
Графический метод решения систем уравнений Решение примеров в пределах 10
Решение примеров в пределах 10 Множення і ділення
Множення і ділення Мир многогранников
Мир многогранников