Содержание
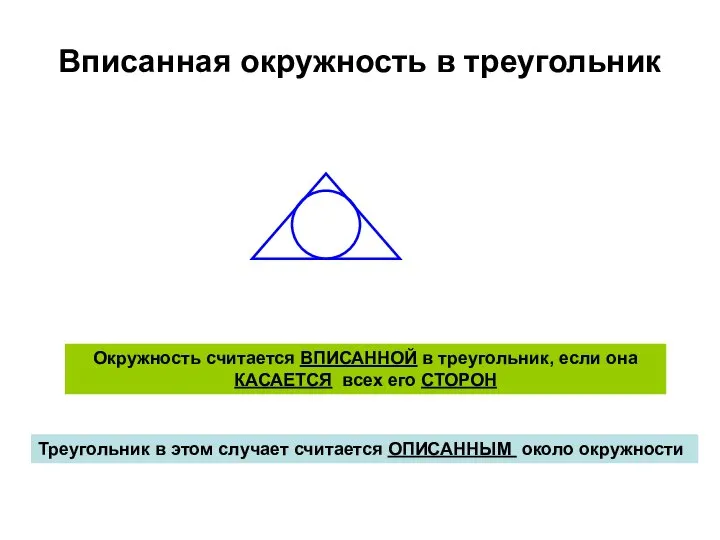
- 2. Вписанная окружность в треугольник Окружность считается ВПИСАННОЙ в треугольник, если она КАСАЕТСЯ всех его СТОРОН Треугольник
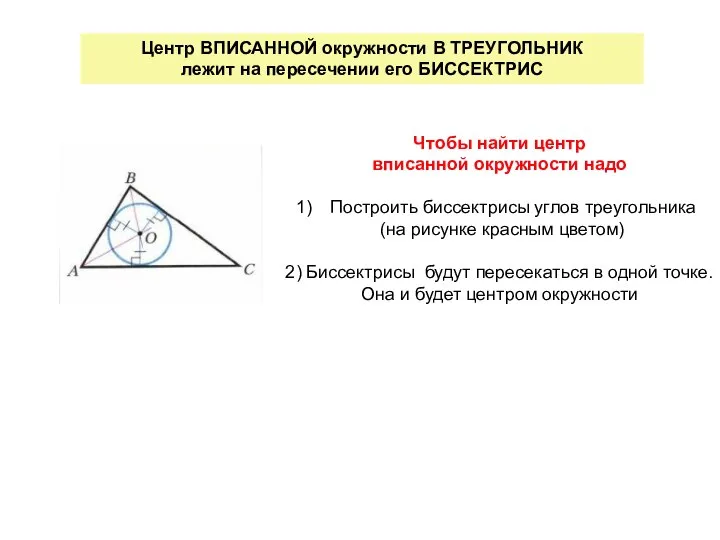
- 3. Центр ВПИСАННОЙ окружности В ТРЕУГОЛЬНИК лежит на пересечении его БИССЕКТРИС Чтобы найти центр вписанной окружности надо
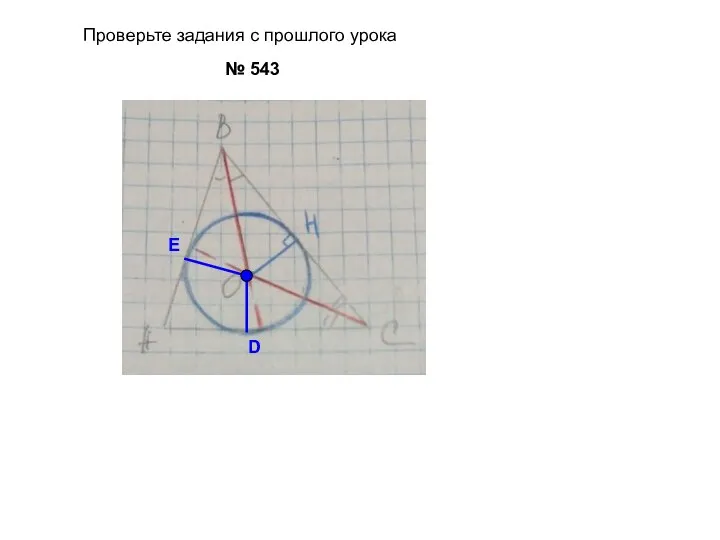
- 4. № 543 E D Проверьте задания с прошлого урока
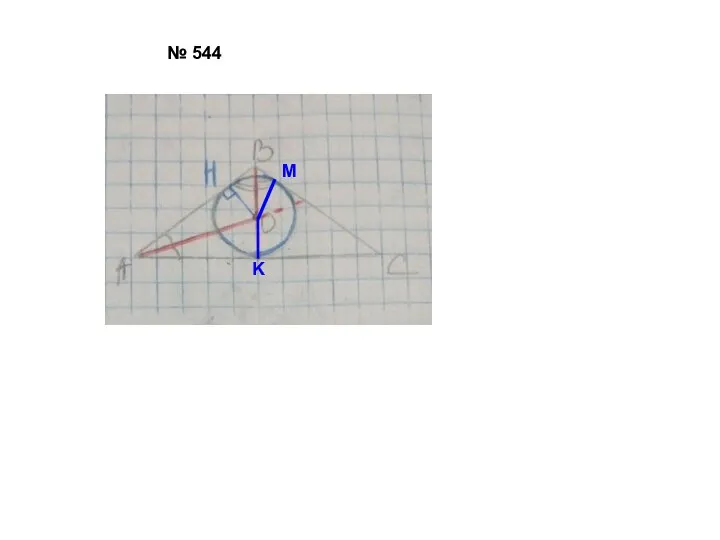
- 5. № 544 K M
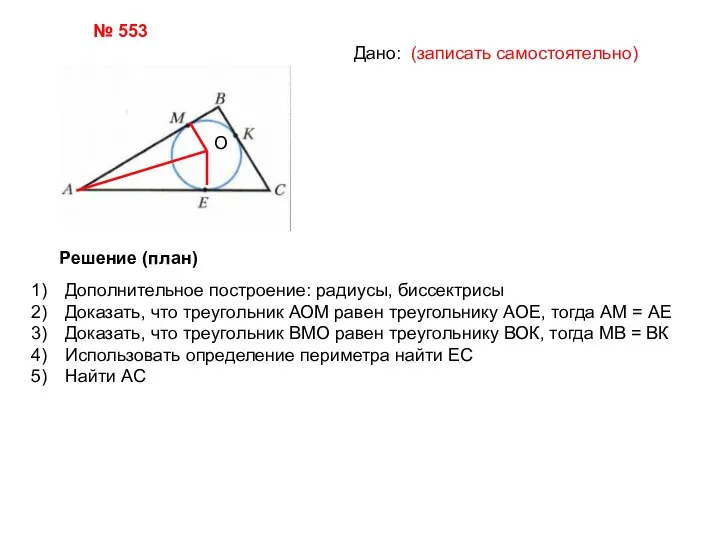
- 6. № 553 Дано: (записать самостоятельно) Решение (план) О Дополнительное построение: радиусы, биссектрисы Доказать, что треугольник АОМ
- 8. Скачать презентацию
 Сумма углов треугольника
Сумма углов треугольника Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Производные функции нескольких переменных (часть 1)
Производные функции нескольких переменных (часть 1) Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3
Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3 Геометрия прически
Геометрия прически Сравнение множеств
Сравнение множеств Презентация на тему Уравнение множественной регрессии
Презентация на тему Уравнение множественной регрессии  Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Линейное уравнение с одной переменной. Подготовка к контрольной работе
Линейное уравнение с одной переменной. Подготовка к контрольной работе Прогрессии в физике
Прогрессии в физике Математические правила и законы
Математические правила и законы Признаки параллельности прямых
Признаки параллельности прямых Параллельность плоскостей
Параллельность плоскостей Мир функций и графиков. Урок - аукцион
Мир функций и графиков. Урок - аукцион Задачи на дроби (повторение)
Задачи на дроби (повторение) Координатная плоскость. Прямоугольная система координат
Координатная плоскость. Прямоугольная система координат Умножение и деление смешанных чисел
Умножение и деление смешанных чисел ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола
ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола 04.17.21.00[1]
04.17.21.00[1] Многогранники. Решение задач
Многогранники. Решение задач Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Анализ геометрических высказываний
Анализ геометрических высказываний Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Линейная функция. Задания
Линейная функция. Задания Параллелограмм. Свойства параллелограмма. Трапеция
Параллелограмм. Свойства параллелограмма. Трапеция Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Метрология. Стандартизация
Метрология. Стандартизация Презентация на тему Квадратные уравнения 8 класс
Презентация на тему Квадратные уравнения 8 класс