Содержание
- 2. Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. Пьер Симон Лаплас
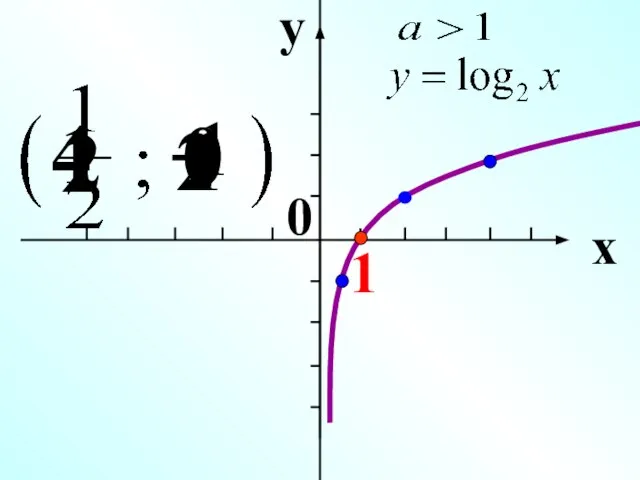
- 3. y = logax Логарифмическая функция
- 4. y x -1 1 0 2 1 4 2 1 0
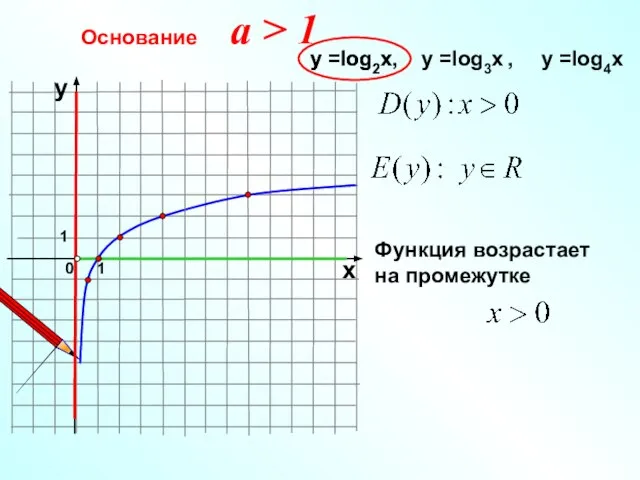
- 5. Основание 1 0 х у у =log2x, у =log3x , у =log4x у =log2x a >
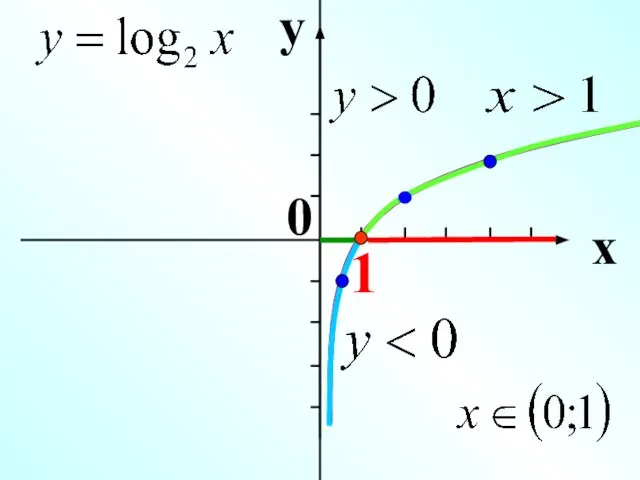
- 6. y x 1 0
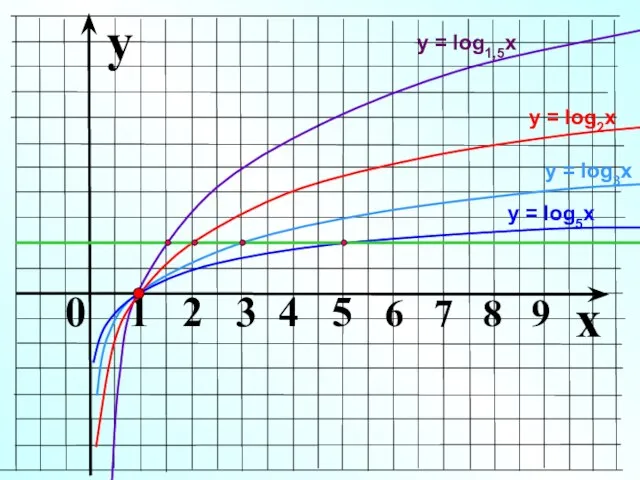
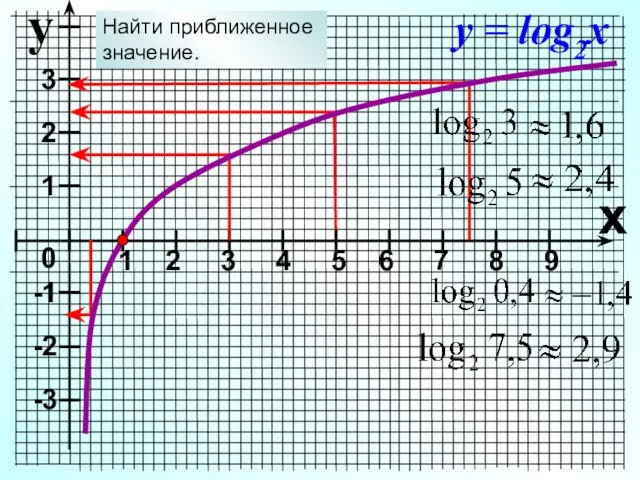
- 7. y 0 1 2 3 4 5 6 7 8 9 x
- 8. y х 1 2 3 4 5 6 7 8 9 3 2 1 0 -1
- 9. y x 0 1 1 0 2 -1 4 -2 1 0
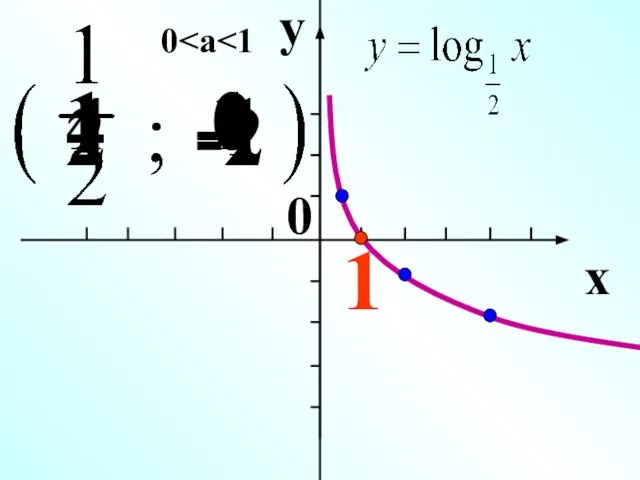
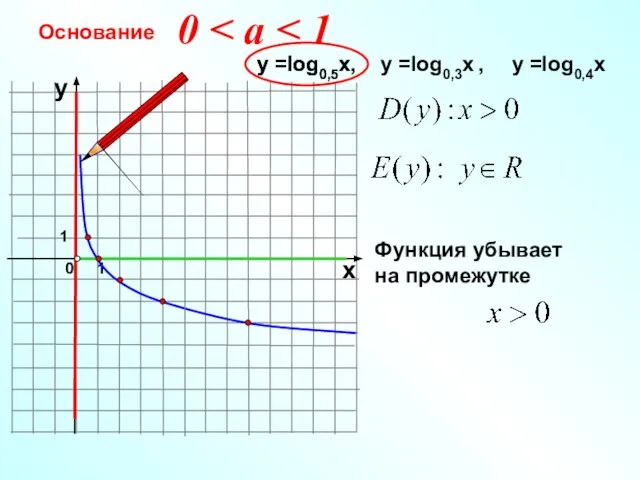
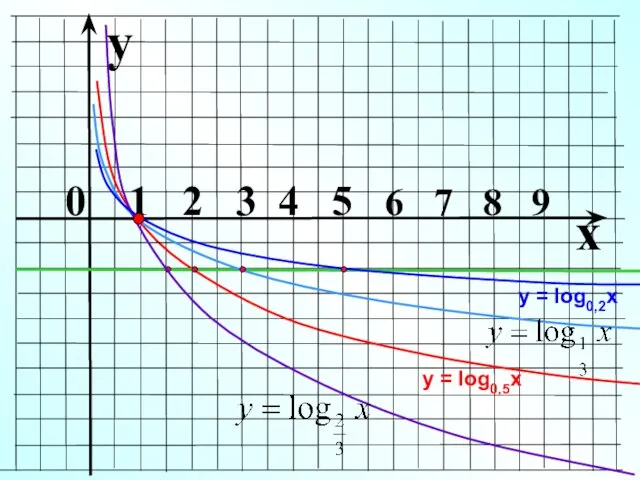
- 10. Основание 1 0 х у у =log0,5x, у =log0,3x , у =log0,4x у =log0,5x 0 1
- 11. y x 0 1 x =1 0
- 12. y x 0 1 2 3 4 5 6 7 8 9
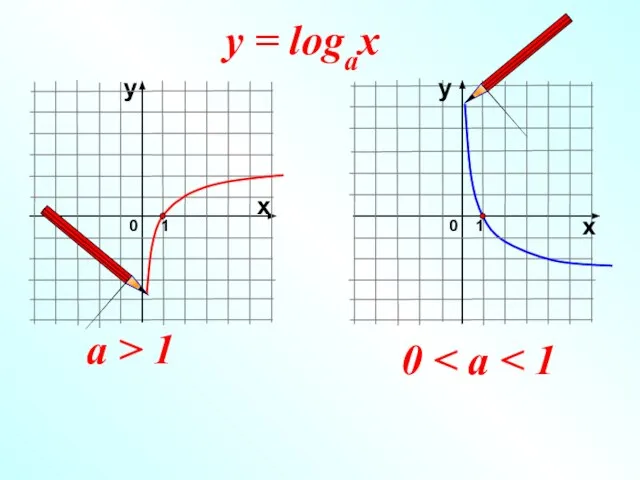
- 13. у 0 1 х 0 1 х у a > 1 0 y = logax
- 14. log3 log3 2,7 4 можно выполнить, используя свойство возрастания или убывания логарифмической функции Сравнение чисел т.к.
- 15. 1 > функция у = log3x возраст. 0 23 1 1
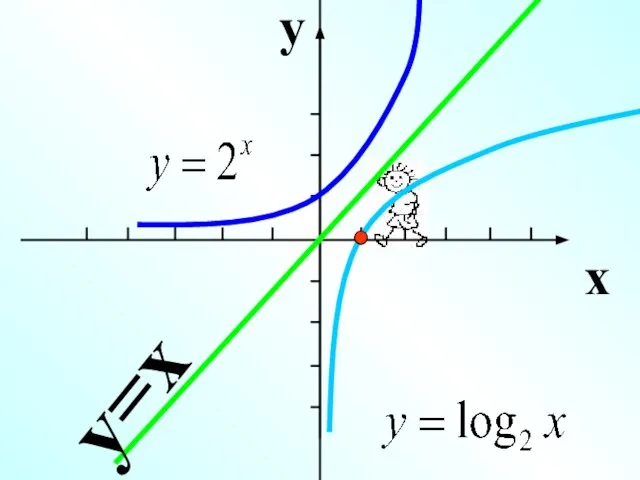
- 16. y x y=x
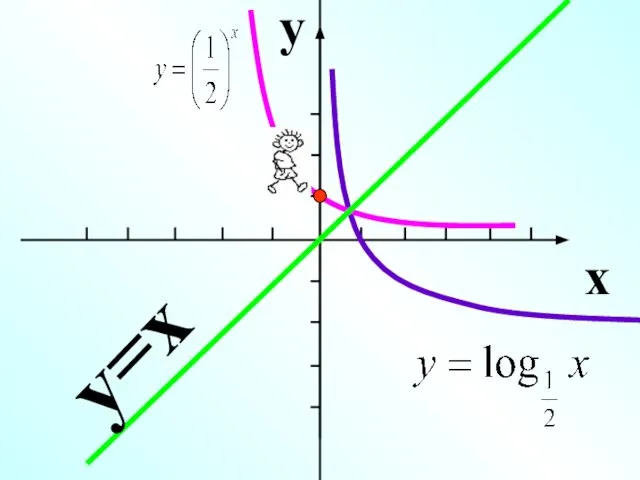
- 17. y x y=x
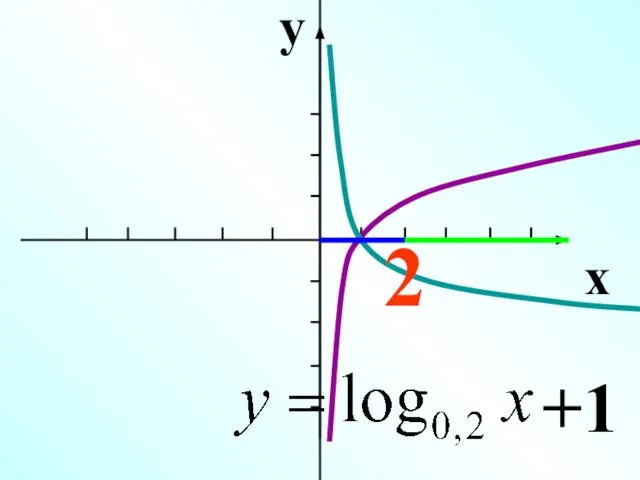
- 18. y x 2 +1
- 19. y x -2
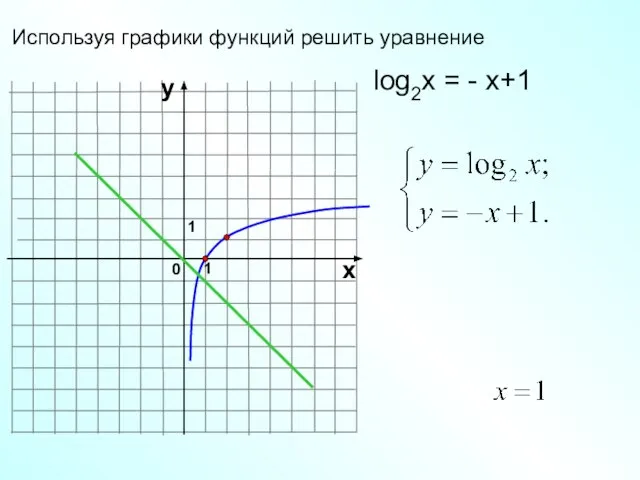
- 20. Используя графики функций решить уравнение 1 0 х у 1 log2x = - x+1
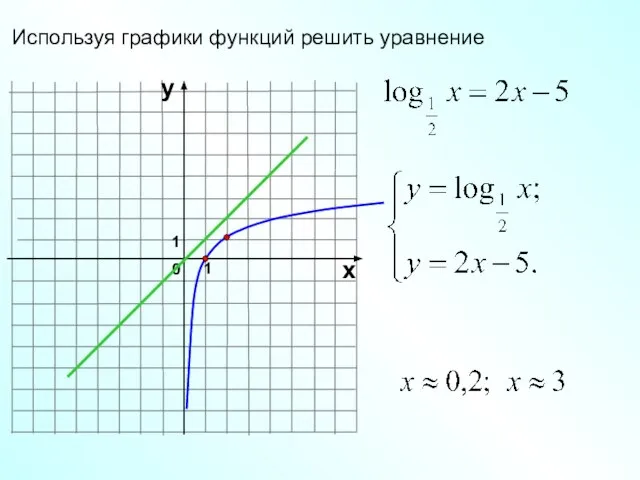
- 21. Используя графики функций решить уравнение 1 0 х у 1
- 22. 1 0 х у 1 Используя графики функций решить неравенство
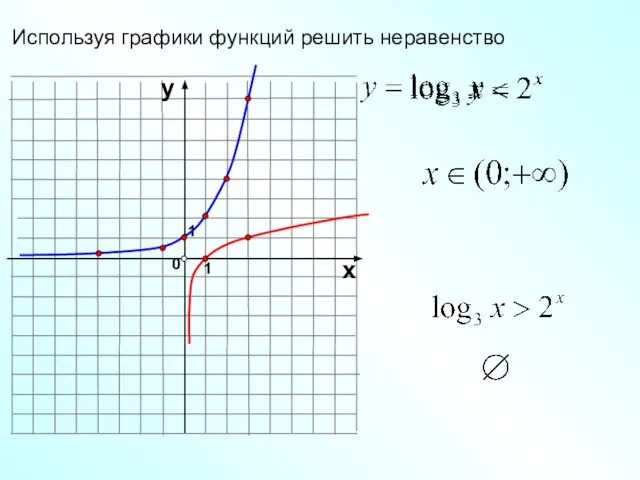
- 23. 1 0 х у 1 Используя графики функций решить неравенство
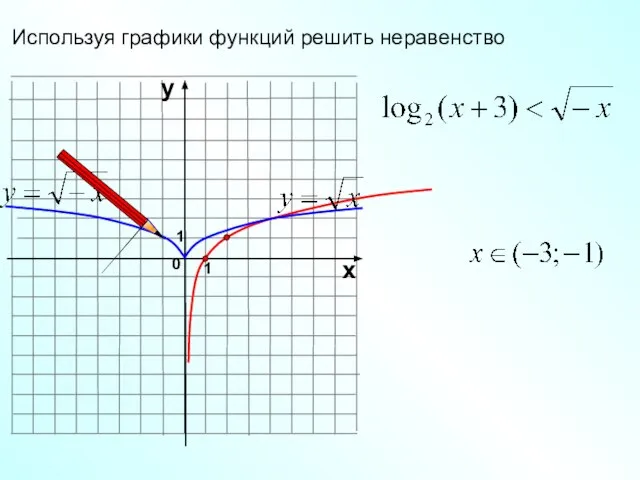
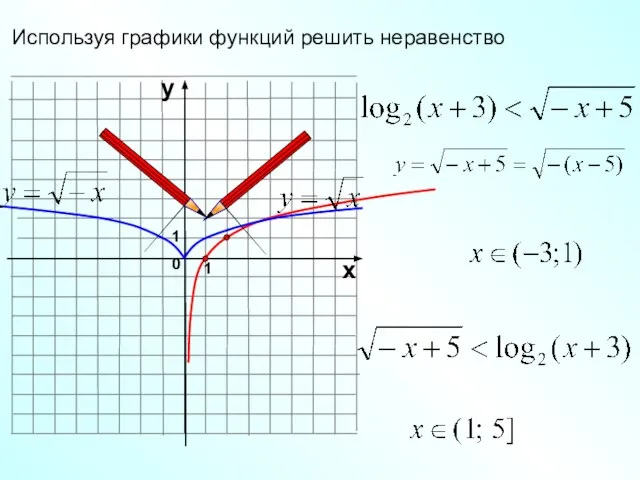
- 24. 1 0 х у 1 Используя графики функций решить неравенство
- 26. Скачать презентацию


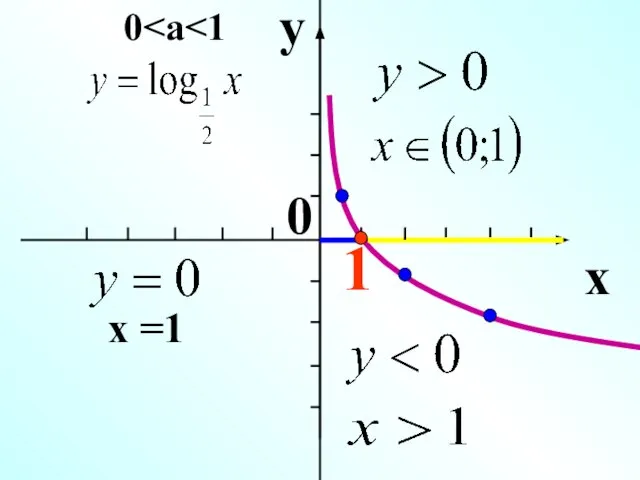


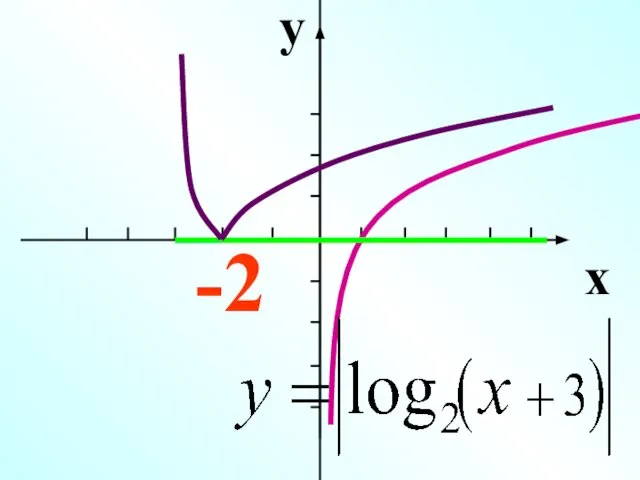
 Куб. Параллелепипед. Тест
Куб. Параллелепипед. Тест Обратные тригонометрические функции
Обратные тригонометрические функции Презентация на тему Умножение и деление на 10
Презентация на тему Умножение и деление на 10  Концентрация. Часть II
Концентрация. Часть II Добери знак
Добери знак Разложение разности квадратов на множители
Разложение разности квадратов на множители Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)  Показательные уравнения
Показательные уравнения Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Прямой угол
Прямой угол Решение задач
Решение задач Ловушка фиктивных переменных
Ловушка фиктивных переменных Решение линейных неравенств
Решение линейных неравенств Лекция 5_1_СЛАУ_Итерац методы
Лекция 5_1_СЛАУ_Итерац методы Квадратичная функция
Квадратичная функция Презентация на тему Как извлечь корень?
Презентация на тему Как извлечь корень?  Задания со спичками
Задания со спичками Полезные витамины
Полезные витамины Непериодические бесконечные десятичные дроби
Непериодические бесконечные десятичные дроби Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика
Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах Геометрия һәм оригами
Геометрия һәм оригами Квадратный метр и квадратный сантиметр. 3 класс
Квадратный метр и квадратный сантиметр. 3 класс Методика изучения площади
Методика изучения площади Арифметический корень натуральной степени
Арифметический корень натуральной степени Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Формы представления регрессионных уравнений
Формы представления регрессионных уравнений Окружность и круг. Задачи
Окружность и круг. Задачи