Множественный регрессионный анализ

Множественная линейная регрессия
- линейная модель
- i-ое наблюдаемое значение отклика
- i-ые наблюдаемые значения факторов

Множественная линейная регрессия
Модель:
Наблюдения:

Множественная линейная регрессия

Множественная линейная регрессия

Множественная линейная регрессия
- система нормальных уравнений

Множественная линейная регрессия

Множественная линейная регрессия

Интервальные оценки
Оценка остаточной дисперсии

Множественная линейная регрессия
Оценка остаточной дисперсии
Адекватность модели
Оценка общей дисперсии

Полиномиальная регрессия
Замена:
В матричной форме

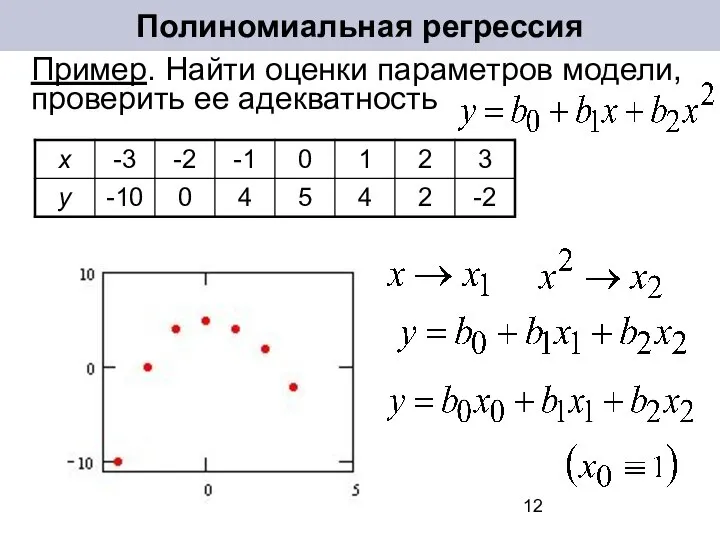
Полиномиальная регрессия
Пример. Найти оценки параметров модели, проверить ее адекватность

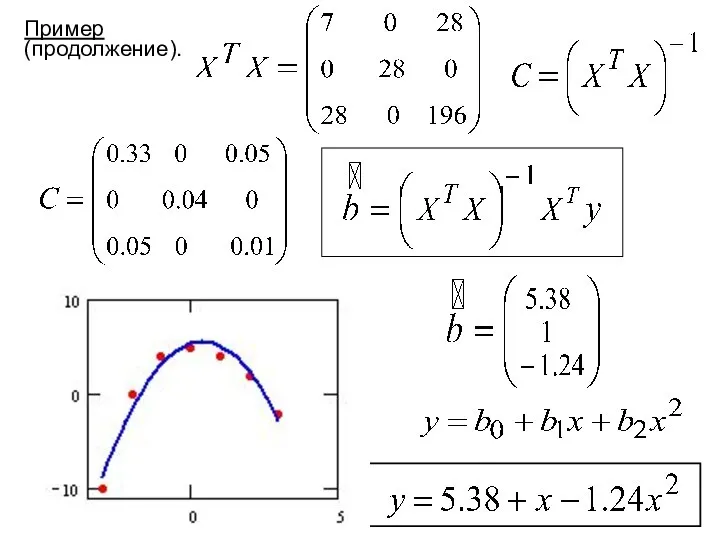
Пример (продолжение).
Перейдем к матричной форме

Пример (продолжение).

Интервальные оценки
Пример (продолжение)