Математическая статистика (лекция 7)

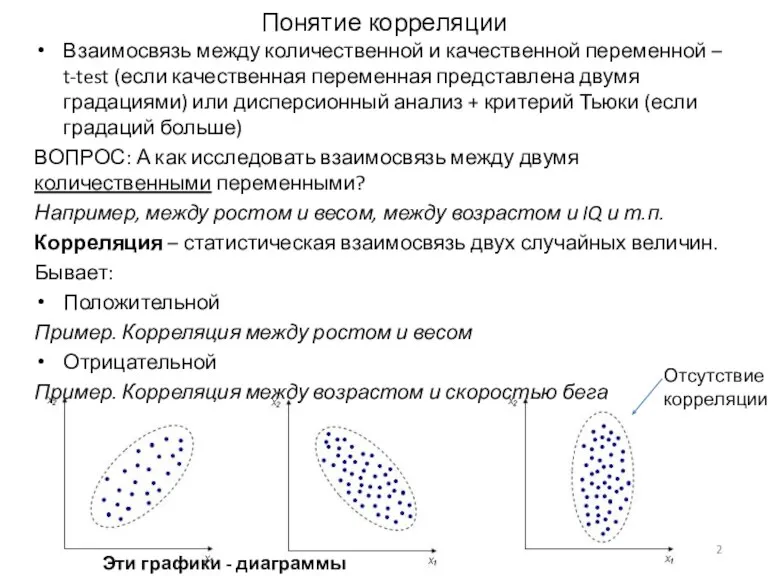
Понятие корреляции
Взаимосвязь между количественной и качественной переменной – t-test (если качественная переменная представлена двумя градациями) или дисперсионный анализ + критерий Тьюки (если градаций больше)
ВОПРОС: А как исследовать взаимосвязь между двумя количественными переменными?
Например, между ростом и весом, между возрастом и IQ и т.п.
Корреляция – статистическая взаимосвязь двух случайных величин.
Бывает:
Положительной
Пример. Корреляция между ростом и весом
Отрицательной
Пример. Корреляция между возрастом и скоростью бега
Эти графики - диаграммы рассеяния
Отсутствие корреляции

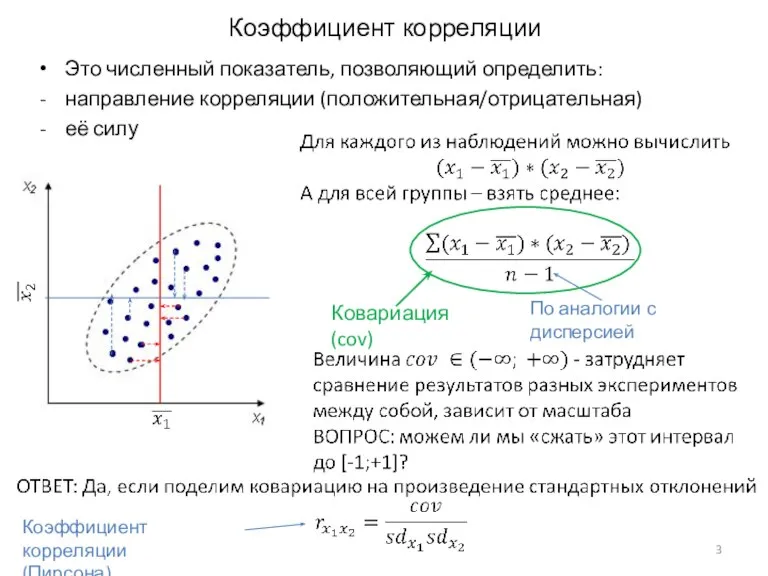
Коэффициент корреляции
Это численный показатель, позволяющий определить:
направление корреляции (положительная/отрицательная)
её силу
По аналогии с дисперсией
Ковариация (cov)
Коэффициент корреляции
(Пирсона)

Почему коэффициент корреляции варьирует на [-1;+1]?
Скалярное произведение векторов A и B
Норма вектора A
Норма вектора B

Коэффициент детерминации R2
Это коэффициент корреляции в квадрате
Всегда неотрицателен и варьирует на [0;1]
R2 – часть изменчивости (дисперсии) переменной, обусловленная её взаимосвязью с другой переменной
Визуализация с сайта http://rpsychologist.com/d3/correlation/

Статистическая значимость коэффициента корреляции Пирсона
С уменьшением N уменьшается и t-значение

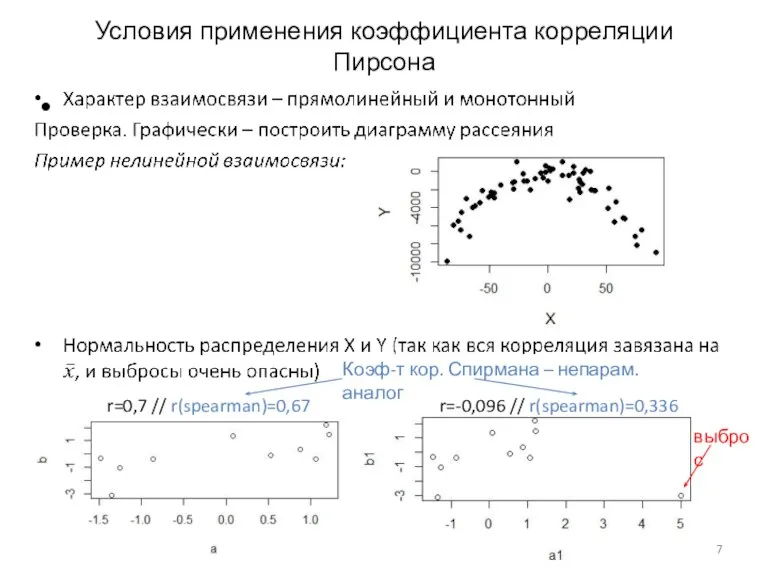
Условия применения коэффициента корреляции Пирсона
выброс
r=0,7 // r(spearman)=0,67
r=-0,096 // r(spearman)=0,336
Коэф-т кор. Спирмана – непарам.аналог

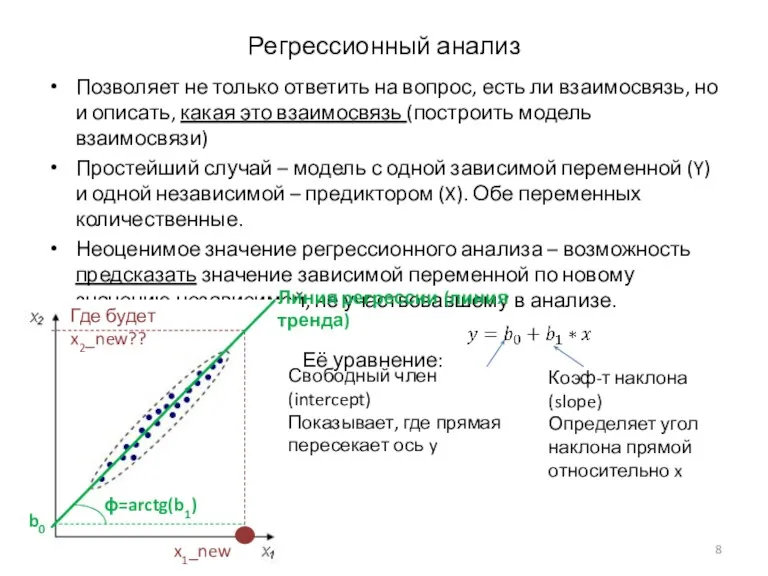
Регрессионный анализ
Позволяет не только ответить на вопрос, есть ли взаимосвязь, но и описать, какая это взаимосвязь (построить модель взаимосвязи)
Простейший случай – модель с одной зависимой переменной (Y) и одной независимой – предиктором (X). Обе переменных количественные.
Неоценимое значение регрессионного анализа – возможность предсказать значение зависимой переменной по новому значению независимой, не участвовавшему в анализе.
Её уравнение:
x1_new
Где будет x2_new??
Линия регрессии (линия тренда)
Свободный член (intercept)
Показывает, где прямая
пересекает ось y
b0
Коэф-т наклона (slope)
Определяет угол наклона прямой относительно x
ϕ=arctg(b1)

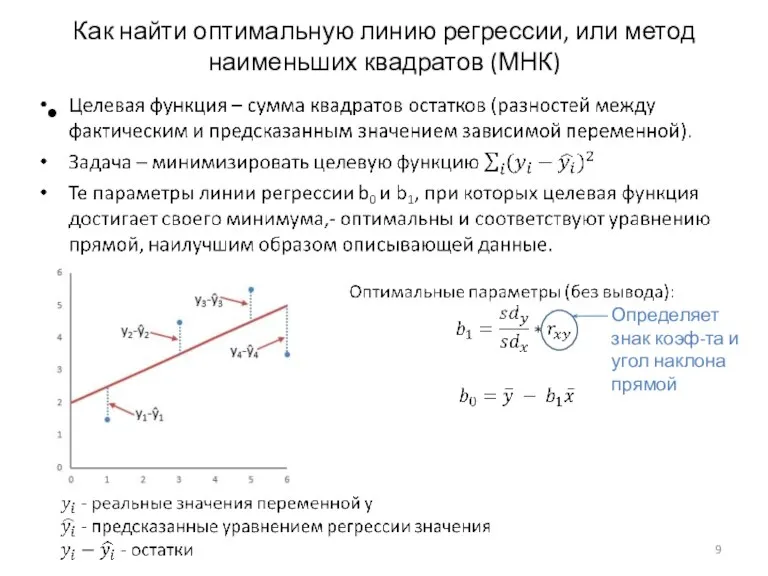
Как найти оптимальную линию регрессии, или метод наименьших квадратов (МНК)
Определяет знак коэф-та и угол наклона прямой

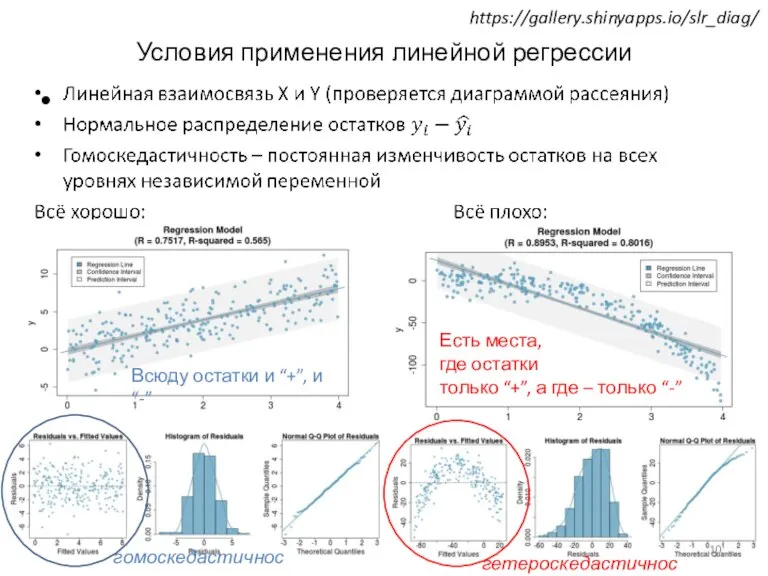
Условия применения линейной регрессии
гомоскедастичность
гетероскедастичность
Всюду остатки и “+”, и “-”
Есть места,
где остатки
только “+”, а где – только “-”
https://gallery.shinyapps.io/slr_diag/

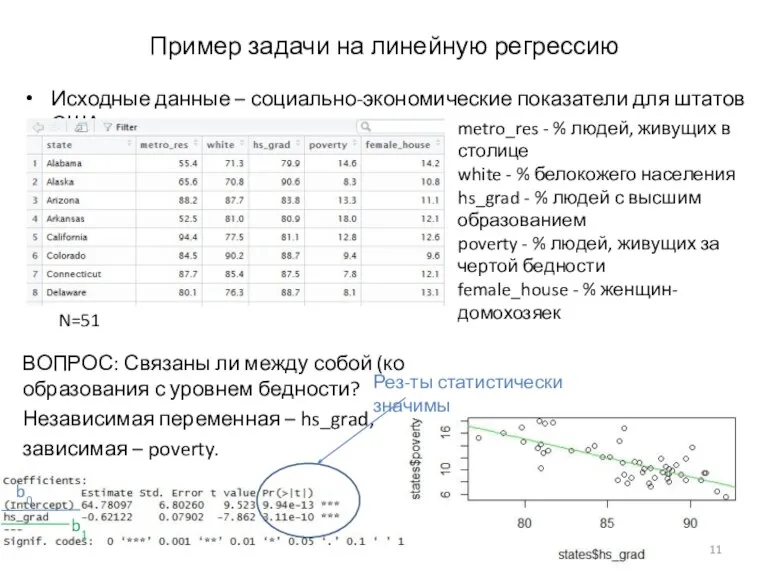
Пример задачи на линейную регрессию
Исходные данные – социально-экономические показатели для штатов США
ВОПРОС: Связаны ли между собой (коррелируют ли) уровень образования с уровнем бедности?
Независимая переменная – hs_grad,
зависимая – poverty.
metro_res - % людей, живущих в столице
white - % белокожего населения
hs_grad - % людей с высшим образованием
poverty - % людей, живущих за чертой бедности
female_house - % женщин-домохозяек
N=51
b0
b1
Рез-ты статистически значимы

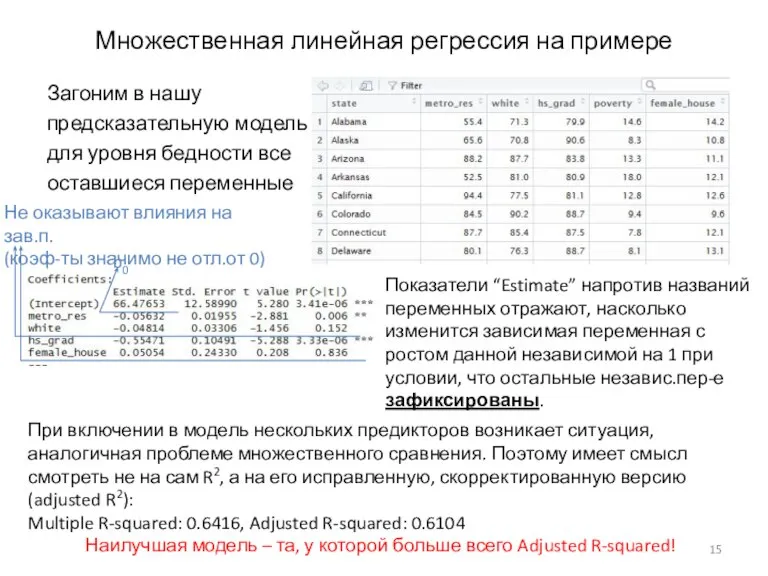
Ещё об интерпретации
b1
Вероятность наблюдать t-значение, равное ±7,862 (или выше), при условии, что верна H0: μ(b1)=0
% бедных
% образованных

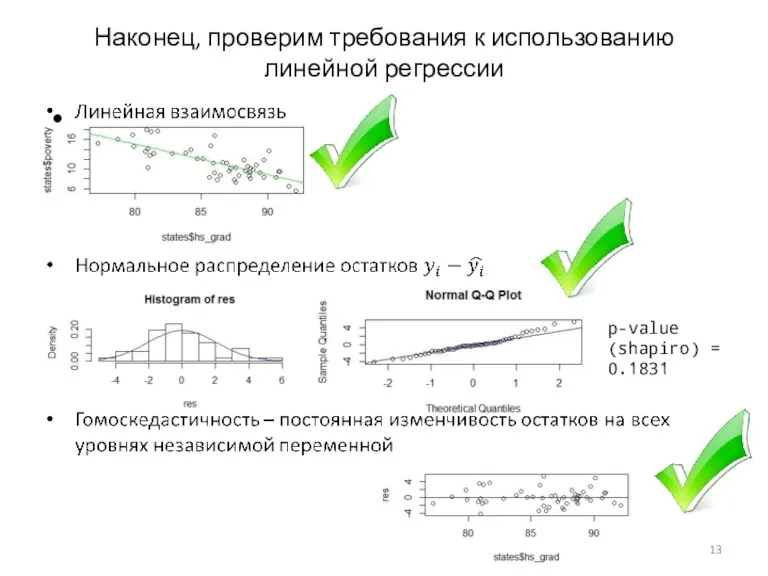
Наконец, проверим требования к использованию линейной регрессии
p-value (shapiro) = 0.1831

Множественная линейная регрессия
Зависимая переменная
Предикторы

Множественная линейная регрессия на примере
Загоним в нашу
предсказательную модель
для уровня бедности все
оставшиеся переменные
b0
Не оказывают влияния на зав.п.
(коэф-ты значимо не отл.от 0)
Показатели “Estimate” напротив названий переменных отражают, насколько изменится зависимая переменная с ростом данной независимой на 1 при условии, что остальные независ.пер-е зафиксированы.
При включении в модель нескольких предикторов возникает ситуация, аналогичная проблеме множественного сравнения. Поэтому имеет смысл смотреть не на сам R2, а на его исправленную, скорректированную версию(adjusted R2):
Multiple R-squared: 0.6416, Adjusted R-squared: 0.6104
Наилучшая модель – та, у которой больше всего Adjusted R-squared!

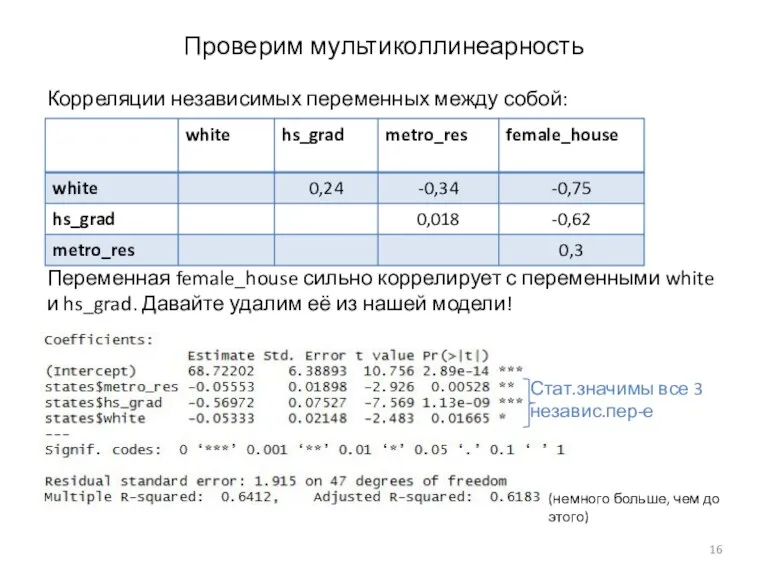
Проверим мультиколлинеарность
Корреляции независимых переменных между собой:
Переменная female_house сильно коррелирует с переменными white и hs_grad. Давайте удалим её из нашей модели!
Стат.значимы все 3 независ.пер-е
(немного больше, чем до этого)

Введение в логистическую регрессию

От вероятности к логарифму шанса

Как подбирать коэффициенты логистической регрессии?
Будем двигаться последовательно, и начнём с модели вовсе без предикторов (intercept-only model).
В качестве тренировочного примера возьмём данные про пассажиров «Титаника» (714 наблюдений). Номинативные переменные:
Выжил/нет (это будет зависимая переменная)
Пол (мужчина/женщина)
Класс каюты (1й класс/2й класс/3й класс)

Модель с одним номинативным предиктором
Теперь будем учитывать ещё и пол пассажира.
Распределение пассажиров по полу и исходу пребывания на Титанике (таблица сопряжённости):
Рассчитаем шанс выжить для мужчин и ываываываыаыаываыва женщин по отдельности:
odds(male)=93/360=0,26
odds(female)=197/64=3,08
Их логарифмы: ln(odds(male))=-1,35
ln(odds(female))=1,12
Отношение шансов выжить для мужчин и женщин = 0,26/3,08=0,08
Его логарифм: ln(odds(male)/odds(female))=ln(odds(male))-ln(odds(female))=-2,47
Уравнение регрессии примет вид:
ln(odds(survive))=1,12-2,47*Sex_male
Логарифм шанса выжить, если пассажир - женщина
b0
«Штраф» (цена перехода), если пассажир мужчина, – логарифм отношения шансов выжить для мужчин и базового уровня фактора (женщин)
b1
Переменная, принимающая значение 0, если пассажир – женщина, и 1 – если мужчина
Какая градация будет базовым уровнем – выбирается просто по алфавиту!

Если независимая переменная - количественная
ЗАДАЧА. Исследовать, как влияет средний балл абитуриента в школе на вероятность его поступления в ВУЗ.
Исходные данные – 400 наблюдений вида
Коэффициенты уравнения регрессии:
завис.пер-я (1 – поступил, 0 –нет)
независ.колич.пер-я (сред.балл в школе, gpa ϵ [2,26;4])
Логарифмы шансов. 1,0511 – насколько увеличится логарифм шанса поступления при увеличении gpa на 1
ось ln(odds)
ось средних баллов (gpa)
4,5
Если ср.балл ≈ 4.5, то ln(p/(1-p))≈0,3
Отсюда p/(1-p)≈ exp(0,3)≈1,35
Отсюда p≈0,57
Вероятность поступить со средним баллом 4,5 равна 0,57.