Содержание
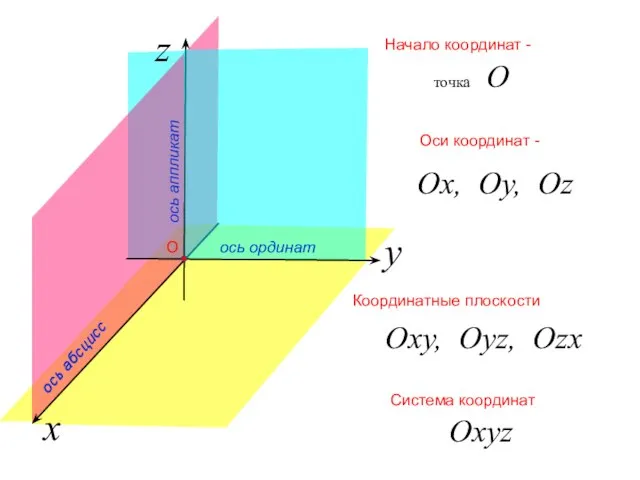
- 2. Прямоугольная система координат в пространстве Если через точку пространства проведены три попарно перпендикулярные прямые, на каждом
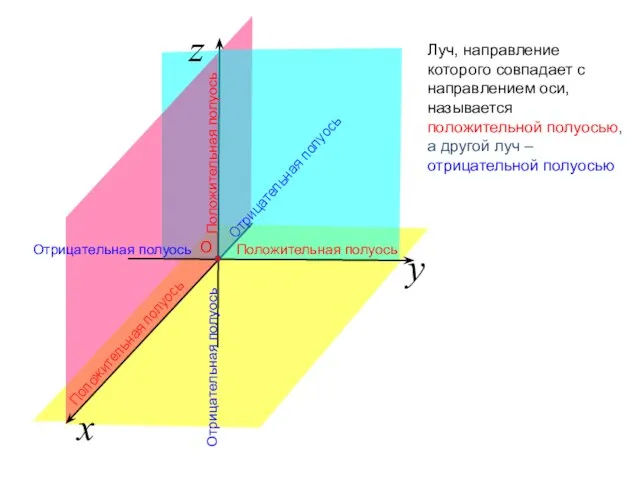
- 4. Определение луча на координатной плоскости. Точка О разделяет каждую из осей координат на два луча. Луч,
- 5. x z y Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч
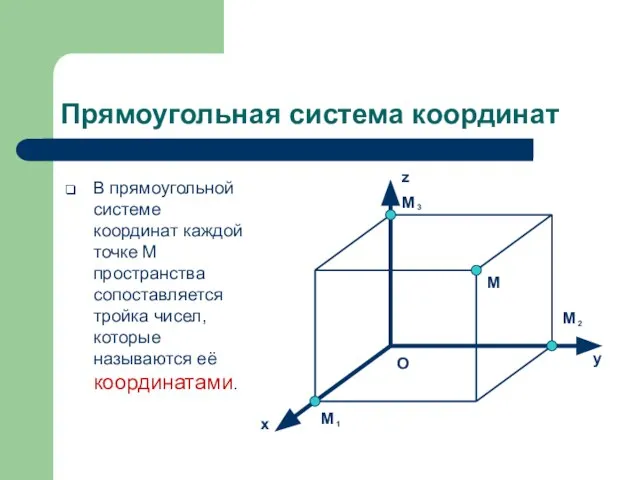
- 6. Прямоугольная система координат В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются
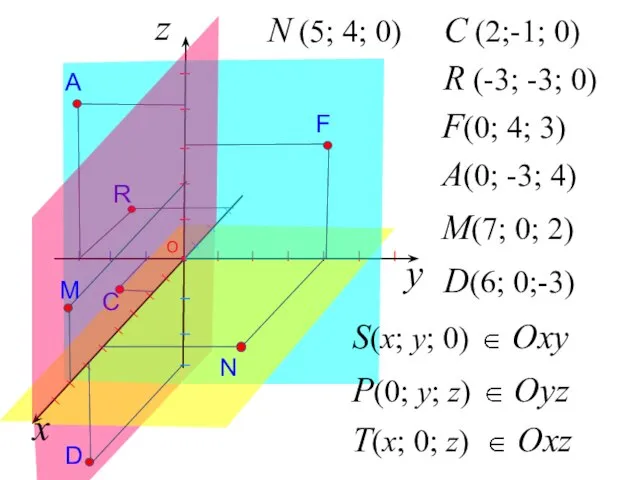
- 7. z N (5; 4; 0) C (2;-1; 0) I I I I I I I I
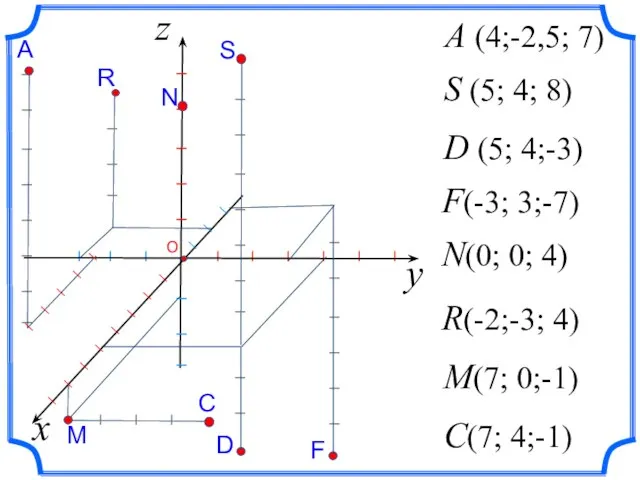
- 8. z A (4;-2,5; 7) S (5; 4; 8) I I I I I I I I
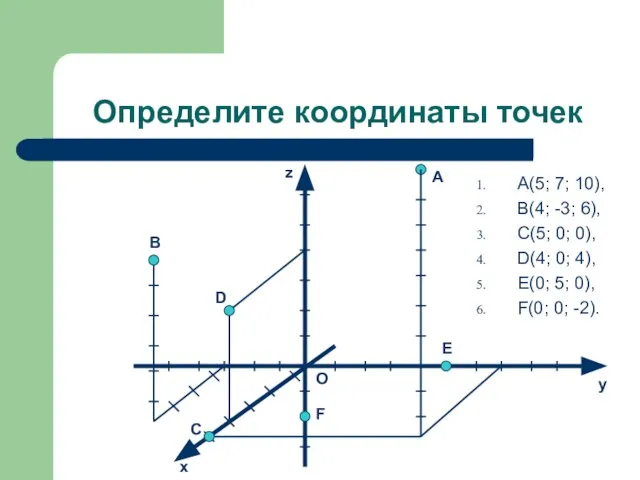
- 9. Определите координаты точек B C O E F D z y x A A(5; 7; 10),
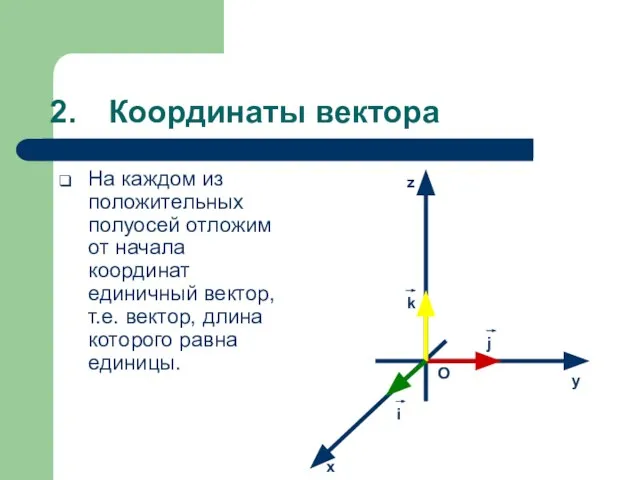
- 10. Координаты вектора На каждом из положительных полуосей отложим от начала координат единичный вектор, т.е. вектор, длина
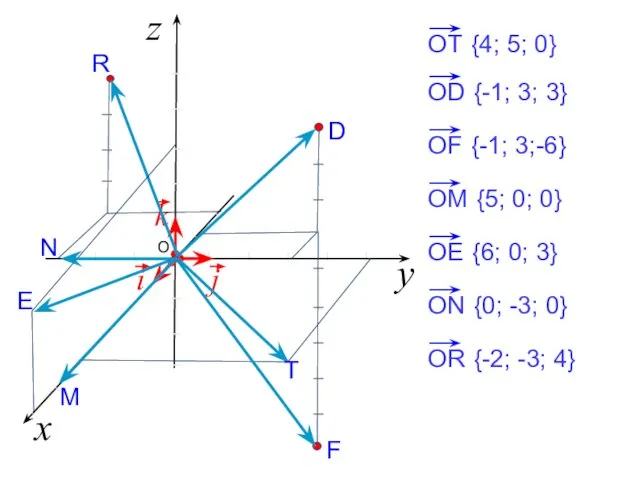
- 11. Связь между координатами векторов и координатами точек. Вектор, конец которого совпадает с данной точкой, а начало
- 12. y x z I I I I I I I I I I I I I
- 13. Разложение по координатным векторам Любой вектор a можно разложить по координатным векторам, т.е. представить в виде
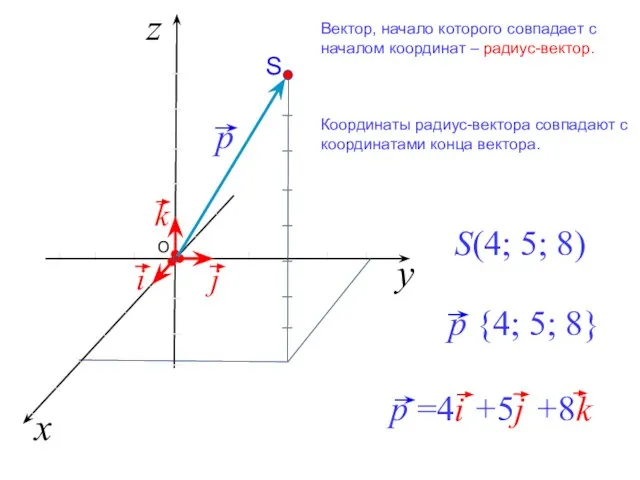
- 14. Вектор, начало которого совпадает с началом координат – радиус-вектор. Координаты радиус-вектора совпадают с координатами конца вектора.
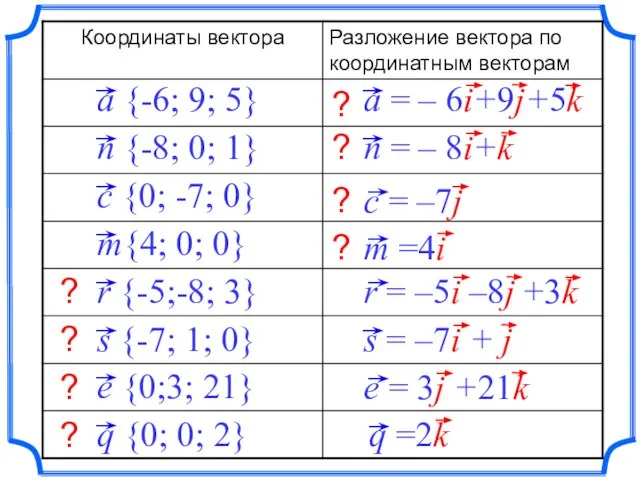
- 15. a {-6; 9; 5} n {-8; 0; 1} m{4; 0; 0} c {0; -7; 0} ?
- 16. Правила №1 Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Если
- 17. Правило №2 Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если a {x
- 18. Правило №3 Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число.
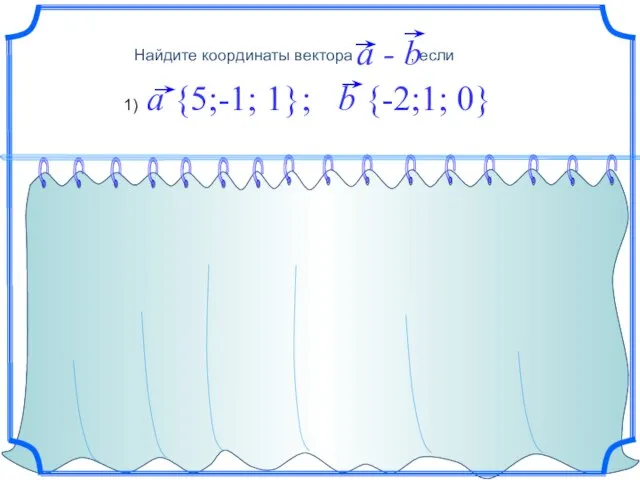
- 19. Найдите координаты вектора , если
- 20. Задача 1 Даны векторы d {-2,7; 3,1; 0,5}
- 21. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. 30
- 22. + Даны векторы Найдите координаты вектора 1) 2) 3) {4;-18;-9}
- 24. Скачать презентацию










 Готовимся к ЕГЭ. Геометрия в3, в6, в9
Готовимся к ЕГЭ. Геометрия в3, в6, в9 Нахождение процентов от числа
Нахождение процентов от числа Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание Применение производной
Применение производной Прямая и окружность
Прямая и окружность Способы построения параллельных прямых
Способы построения параллельных прямых Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Правильные многогранники
Правильные многогранники Возможности символьного вычисления в среде MatLab
Возможности символьного вычисления в среде MatLab Решение примеров
Решение примеров Современный урок: какой он?
Современный урок: какой он? Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе Презентация на тему Разность квадратов
Презентация на тему Разность квадратов  Графический способ решения систем уравнений
Графический способ решения систем уравнений Таблица умножения и деления с числом 7
Таблица умножения и деления с числом 7 Решение задач ОГЭ. Реальная математика, № 16
Решение задач ОГЭ. Реальная математика, № 16 Логарифмические уравнения
Логарифмические уравнения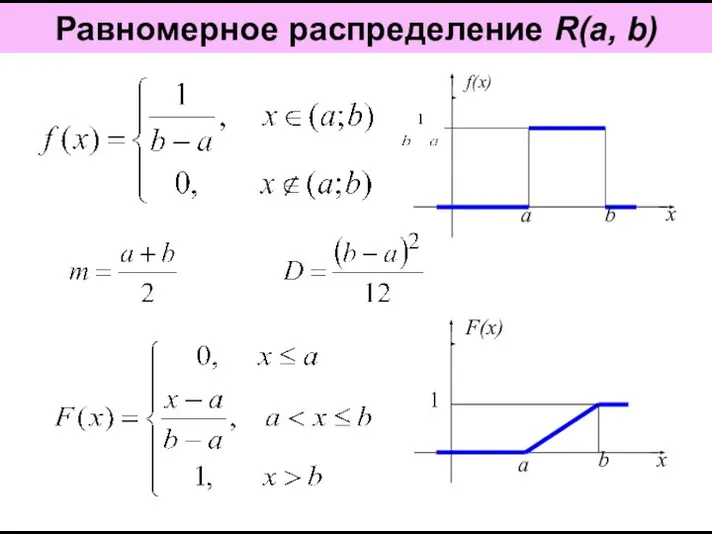 Равномерное распределение R(a, b)
Равномерное распределение R(a, b) Презентация на тему Решение текстовых задач различными способами
Презентация на тему Решение текстовых задач различными способами  Задачи математической статистики. Обработка данных
Задачи математической статистики. Обработка данных Презентация на тему Умножение и деление десятичных дробей на натуральные числа
Презентация на тему Умножение и деление десятичных дробей на натуральные числа  Разложение квадратного трёхчлена на множители
Разложение квадратного трёхчлена на множители Задачи по математике. 1 класс
Задачи по математике. 1 класс Презентация на тему ИЗМЕНЕНИЕ ВЕЛИЧИН
Презентация на тему ИЗМЕНЕНИЕ ВЕЛИЧИН  Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Наибольшее и наименьшее значение функции. Примеры
Наибольшее и наименьшее значение функции. Примеры