- Главная
- Математика
- Багдадская математическая школа

Содержание
- 2. Одним из первых крупных ученых-энциклопедистов Багдадской школы был ал-Кинди (800-879). Он работал в Багдаде и написал
- 3. Однако самым выдающимся математиком IX века, прославившим Багдадскую математическую школу, был ал-Хорезми (783 – ок. 850).
- 4. В Доме мудрости ал-Хорезми не только проводил глубокие математические исследования, но и был талантливым организатором науки.
- 5. Алгебраический трактат ал-Хорезми озаглавлен « Китаб мухтасар ал-Джебр вал-Мукабала»(книга о восстановлении и противопоставлении). В этом трактате
- 10. В 970-1170 г. нарождающуюся алгебру ал- Хорезми и Абу-Камила вознесли на ещё большую высоту ал-Караджи(Караги) и
- 13. Среди них особая роль принадлежит Омару Хайяму – персидскому и таджикскому поэту, философу, астроному и математику.
- 15. Многие арабские математики Багдадской школы перевели наиболее известные труды греческих и индийских математиков и дали комментарии
- 17. Скачать презентацию
Слайд 2Одним из первых крупных ученых-энциклопедистов Багдадской школы был ал-Кинди (800-879). Он работал
Одним из первых крупных ученых-энциклопедистов Багдадской школы был ал-Кинди (800-879). Он работал

в Багдаде и написал около двухсот работ, посвященных различным областям знаний – геометрии, астрономии, оптике, метеорологии, медицине, музыке. Он подчеркивал роль математических и естественных наук в научном познании и утверждал, что философия невозможна без знания математики.
Слайд 3Однако самым выдающимся математиком IX века, прославившим Багдадскую математическую школу, был ал-Хорезми
Однако самым выдающимся математиком IX века, прославившим Багдадскую математическую школу, был ал-Хорезми

(783 – ок. 850). Он родился в Хорезме и получил от отца, одного из просвещенных людей своего времени, необходимое первоначальное образование, которое продолжил в купном городе восточного региона халифата – Мерве. Будучи талантливым и многообещающим молодым ученым, ал-Хорезми уже в начале IX века был привлечён к окружению ал-Мамуна, сына халифа ал-Рашида. В 813 г. после смерти отца ал-Мамун стал халифом. Переехав в 818 г. в Багдад, он пригласил в столицу халифата наиболее известных ученых, в том числе ал-Хорезми. Ему было поручено заведовать книгохранилищем в Байт ал хикма( Доме Мудрости), игравшем в IX-XII веках роль Академии наук халифат.
Слайд 4В Доме мудрости ал-Хорезми не только проводил глубокие математические исследования, но и
В Доме мудрости ал-Хорезми не только проводил глубокие математические исследования, но и

был талантливым организатором науки. Он возглавлял три экспедиции в различные области халифата, руководил работой ученых различных отраслей знаний, приглашенных их разных стран.
Именно в Багдаде ал-Хорезми создал основные всемирно известные труды по математике, астрономии, географии и истории.
После кончины халифа ал-Мамуна ал-Хорезми оставался в Багдаде и пользовался почетом и при других халифах: Мутасиме(833-842) и ал-Васике(842-847).
Наиболее известными математическими и астрономическими трудами ал-Хорезми являются «Арифметический трактат», «Алгебраический трактат», «Извлечения из астрономических таблиц индийцев – синдхинд», «Извлечения из исправленных таблиц хорд Птолемея», «Определение азимута при помощи астролябии», «Книга о мраморных солнечных часах».
Именно в Багдаде ал-Хорезми создал основные всемирно известные труды по математике, астрономии, географии и истории.
После кончины халифа ал-Мамуна ал-Хорезми оставался в Багдаде и пользовался почетом и при других халифах: Мутасиме(833-842) и ал-Васике(842-847).
Наиболее известными математическими и астрономическими трудами ал-Хорезми являются «Арифметический трактат», «Алгебраический трактат», «Извлечения из астрономических таблиц индийцев – синдхинд», «Извлечения из исправленных таблиц хорд Птолемея», «Определение азимута при помощи астролябии», «Книга о мраморных солнечных часах».
Слайд 5Алгебраический трактат ал-Хорезми озаглавлен « Китаб мухтасар ал-Джебр вал-Мукабала»(книга о восстановлении и
Алгебраический трактат ал-Хорезми озаглавлен « Китаб мухтасар ал-Джебр вал-Мукабала»(книга о восстановлении и

противопоставлении). В этом трактате впервые алгебра рассматривается как самостоятельный раздел математики. В латинском переводе слово «ал-джебр» приобрело форму «алгебра» и стало впоследствии названием целого раздела математики. А латинизированное ал-Хорезми – Algorithmi(алгоритм) постепенно стало обозначать любой вычислительный процесс, осуществляемый по определенным правилам. Таким образом было увековечено имя этого великого арабского ученого.
Слайд 10В 970-1170 г. нарождающуюся алгебру ал- Хорезми и Абу-Камила вознесли на ещё
В 970-1170 г. нарождающуюся алгебру ал- Хорезми и Абу-Камила вознесли на ещё

большую высоту ал-Караджи(Караги) и Омар Хайям( Гиясэддин) и их ученики.
Ал-Караджи (ум. в 1016) является автором многих очень важных работ: «Достаточная книга о науке арифметике», « Ал-Фахри»(алгебраический трактат, посвященный визирю Багдада Фахру ал-Мулку), «Ал-Бади»(исследование неопределенных уравнений).
В книге по арифметике ал-Караджи систематизировал результаты трудов арабских математиков Абул-л-Вафа (940-998), ал- Уклидизи (ок. 954-953) и ан-Насави. Это – учебник практической арифметики, аналогичный трактату Абу-л-Вафа « Книга по арифетике для писцов и торговцев», в которой он подробно рассмотрел теорию дробей.
Ал-Караджи (ум. в 1016) является автором многих очень важных работ: «Достаточная книга о науке арифметике», « Ал-Фахри»(алгебраический трактат, посвященный визирю Багдада Фахру ал-Мулку), «Ал-Бади»(исследование неопределенных уравнений).
В книге по арифметике ал-Караджи систематизировал результаты трудов арабских математиков Абул-л-Вафа (940-998), ал- Уклидизи (ок. 954-953) и ан-Насави. Это – учебник практической арифметики, аналогичный трактату Абу-л-Вафа « Книга по арифетике для писцов и торговцев», в которой он подробно рассмотрел теорию дробей.
Слайд 13Среди них особая роль принадлежит Омару Хайяму – персидскому и таджикскому поэту,
Среди них особая роль принадлежит Омару Хайяму – персидскому и таджикскому поэту,

философу, астроному и математику. Он родился в местечке Нишапур, получил блестящее образование, был при дворе правителя Бухары Шамс аль-Мулька, затем – придворным персидского султана Исфагана-Мелакшаха, предоставившего Омару Хайяму обсерваторию, но славу этому ученому обеспечили его выдающиеся труды в области алгебры и геометрии и знаменитые «Рубаи» - около тысячи четверостиший на персидском языке.
Омар Хайям – первый среди математиков, создавший геометрическую теорию решения уравнений 3-й степени и давший о трактате «О доказательстве задач алгебры и алмукабалы» общую классификацию всех уравнений. Он впервые дал геометрическое объяснения решения алгебраических уравнений. Его трактат « Комментарии к трудным постулатам книги Евклида» явился серьезным шагом к созданию неевклидовой геометрии.
Омар Хайям – первый среди математиков, создавший геометрическую теорию решения уравнений 3-й степени и давший о трактате «О доказательстве задач алгебры и алмукабалы» общую классификацию всех уравнений. Он впервые дал геометрическое объяснения решения алгебраических уравнений. Его трактат « Комментарии к трудным постулатам книги Евклида» явился серьезным шагом к созданию неевклидовой геометрии.
Слайд 15Многие арабские математики Багдадской школы перевели наиболее известные труды греческих и индийских
Многие арабские математики Багдадской школы перевели наиболее известные труды греческих и индийских

математиков и дали комментарии к ним. Ибн-Корра (836-901) перевел «Начала» на арабский язык и да комментарий к ним. Он ознакомил арабских ученых с сочинением Архимеда «О правильном семиугольнике». Ал-Джаухари (IX в) дал комментарий к пятой книге «Начал» Евклида. Пытался доказать пятый постулат. Ал-Кухи (X в.) дал комментарии к «Началам» Евклида и к сочинению Архимеда «О шаре и цилиндре».
Ал-Джили (ок. 971-1029) сочинил труд «Принципы индийского счета».
- Предыдущая
Шаблон проекта IoT AcademyСледующая -
Культура общения с людьми с инвалидностью





 Сумма углов геометрических фигур
Сумма углов геометрических фигур Презентация на тему Параллельный перенос и Поворот
Презентация на тему Параллельный перенос и Поворот  Гомотетия. Подобие фигур
Гомотетия. Подобие фигур Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр и наклонные. Угол между прямой и плоскостью Вероятность события (часть 1)
Вероятность события (часть 1) Правильные многогранникик
Правильные многогранникик Конустун бетинин аянты
Конустун бетинин аянты Свойства тригонометрических функций
Свойства тригонометрических функций Разряды чисел
Разряды чисел Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности
Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Арифметический диктант
Арифметический диктант Элементы математической логики
Элементы математической логики Додавання і віднімання мішаних чисел
Додавання і віднімання мішаних чисел Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Координаты вектора
Координаты вектора Приближенные формулы Лапласа и Пуассона
Приближенные формулы Лапласа и Пуассона Задачи. Геометрия 8 кл
Задачи. Геометрия 8 кл Математика в профессии сварщика
Математика в профессии сварщика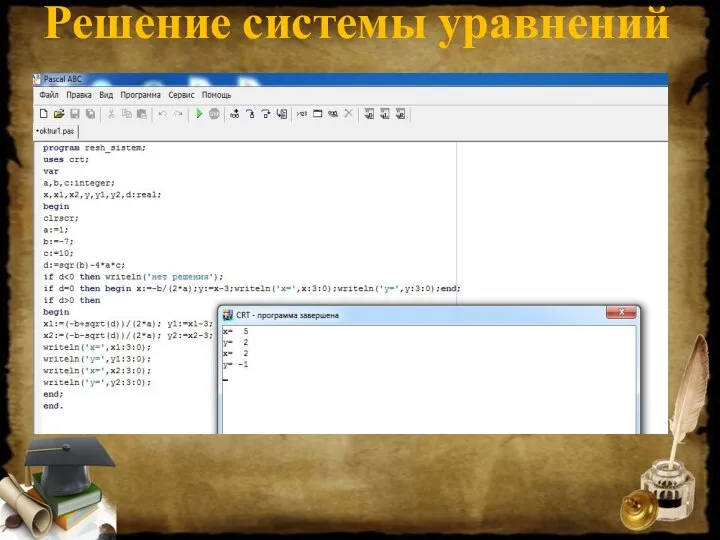 Решение системы уравнений. Задача на странный сюжет
Решение системы уравнений. Задача на странный сюжет Работа над ошибками СОР. Подготовка к СОЧ
Работа над ошибками СОР. Подготовка к СОЧ Показательная функция и ее применение
Показательная функция и ее применение Викторина по геометрии
Викторина по геометрии Геометрия в искусстве
Геометрия в искусстве Формулы сокращенного умножения. Разность квадратов
Формулы сокращенного умножения. Разность квадратов Презентация на тему Статистика и вероятность
Презентация на тему Статистика и вероятность  Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана
Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана Векторы. Тест
Векторы. Тест