Содержание
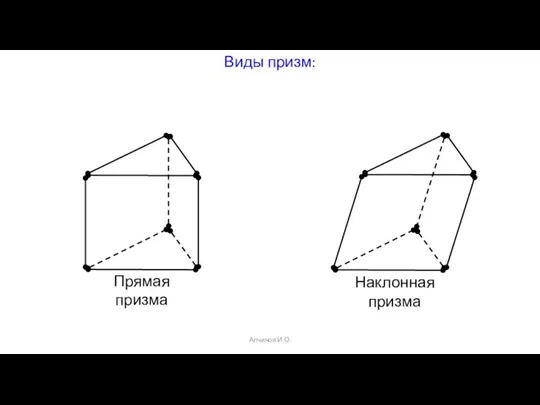
- 2. Алчинов И.О. Виды призм: Прямая призма Наклонная призма
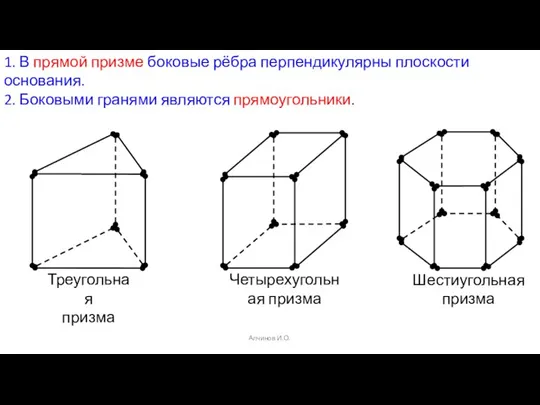
- 3. Алчинов И.О. 1. В прямой призме боковые рёбра перпендикулярны плоскости основания. 2. Боковыми гранями являются прямоугольники.
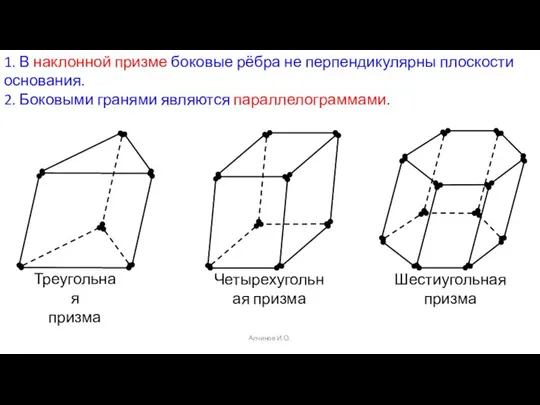
- 4. Алчинов И.О. 1. В наклонной призме боковые рёбра не перпендикулярны плоскости основания. 2. Боковыми гранями являются
- 5. Алчинов И.О. В основании правильной призмы лежит правильный многоугольник
- 6. Алчинов И.О. Диагональ призмы — это отрезок, который соединяет две вершины, не принадлежащие одной грани.
- 7. Алчинов И.О. Диагональное сечение призмы — это сечение плоскостью, проходящей через два боковых ребра, не принадлежащие
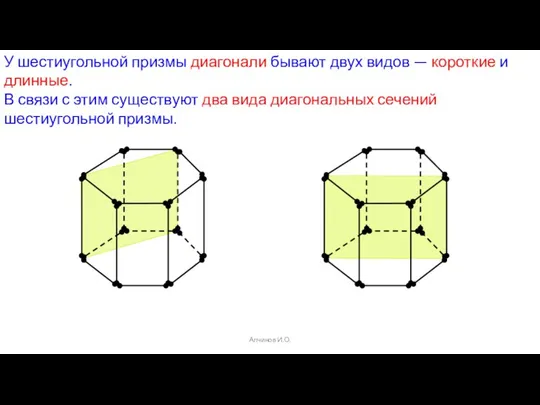
- 8. Алчинов И.О. У шестиугольной призмы диагонали бывают двух видов — короткие и длинные. В связи с
- 9. Алчинов И.О.
- 10. Алчинов И.О. Важные формулы нахождения площади n-угольников
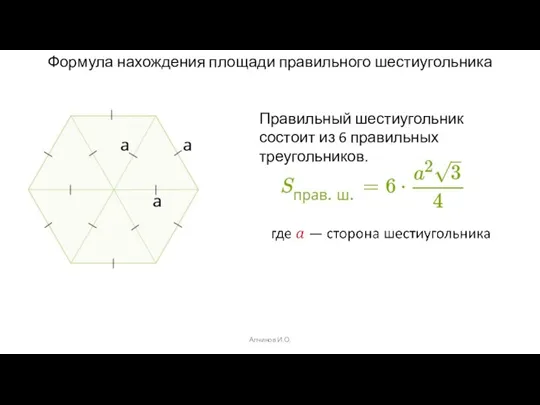
- 11. Алчинов И.О. Формула нахождения площади правильного шестиугольника Правильный шестиугольник состоит из 6 правильных треугольников.
- 12. Алчинов И.О. №6 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое
- 13. Алчинов И.О. №11 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота
- 14. Алчинов И.О. №13 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 15 и 20. Площадь
- 15. Алчинов И.О. Самостоятельная работа №1 1) Нахождение объёма треугольной призмы 2) Нахождение площади боковой поверхности треугольной
- 16. Алчинов И.О. №1 В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см³ воды и погрузили
- 17. Алчинов И.О. №2 В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80
- 18. Алчинов И.О. №8 Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная
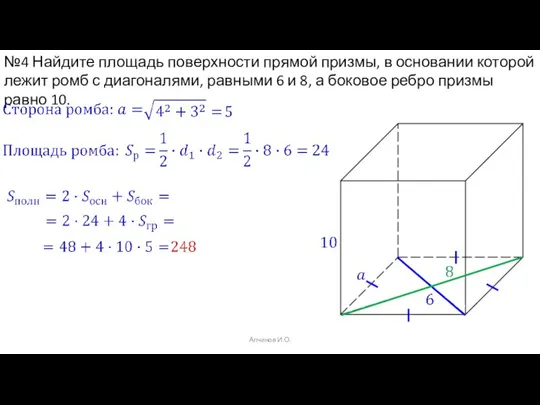
- 19. Алчинов И.О. №4 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными
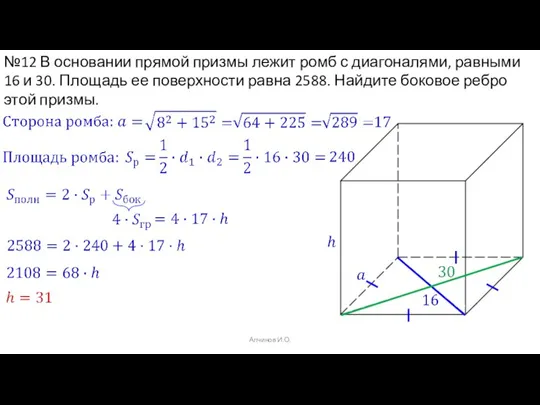
- 20. Алчинов И.О. №12 В основании прямой призмы лежит ромб с диагоналями, равными 16 и 30. Площадь
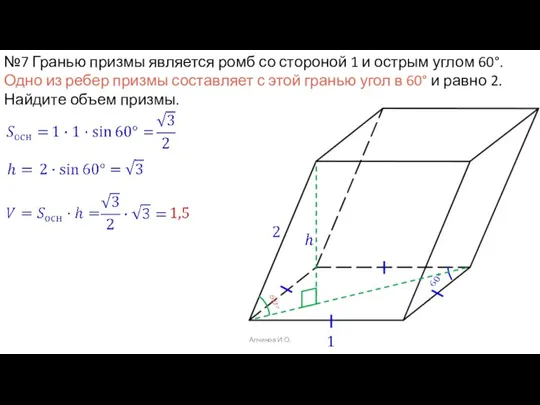
- 21. Алчинов И.О. №7 Гранью призмы является ромб со стороной 1 и острым углом 60°. Одно из
- 22. Алчинов И.О. Самостоятельная работа №2 1) Нахождение объёма четырехугольной призмы 2) Нахождение площади боковой поверхности четырехугольной
- 23. Алчинов И.О. №3 Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а
- 24. Алчинов И.О. №5 Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а
- 25. Алчинов И.О. №10 От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через
- 26. Алчинов И.О. №14 Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой
- 27. Алчинов И.О. №15 Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей
- 28. Алчинов И.О. №16 Найдите объем многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной
- 29. Алчинов И.О. №17 Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, C1 правильной
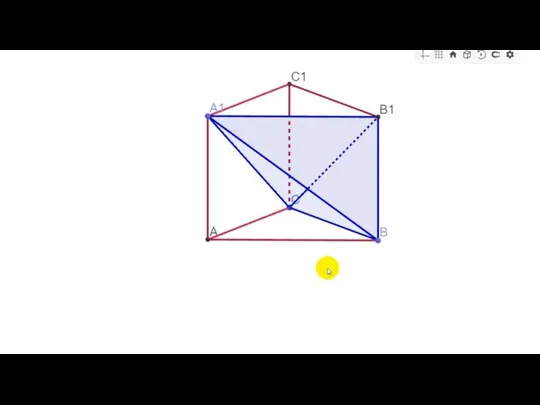
- 30. Алчинов И.О. №18 Найдите объем многогранника, вершинами которого являются точки A1, B1, B, C правильной треугольной
- 31. Алчинов И.О.
- 32. Алчинов И.О. №18 Найдите объем многогранника, вершинами которого являются точки A1, B1, B, C правильной треугольной
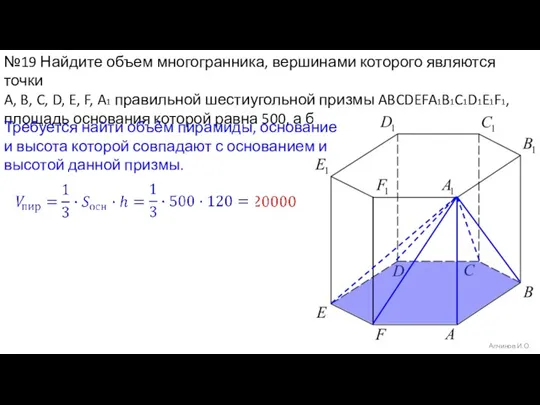
- 33. Алчинов И.О. №19 Найдите объем многогранника, вершинами которого являются точки A, B, C, D, E, F,
- 34. Алчинов И.О. №20 Найдите объем многогранника, вершинами которого являются точки A, B, C,A1, B1, C1 правильной
- 35. Алчинов И.О. №21 Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1,
- 36. Алчинов И.О. №22 Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1,
- 37. Алчинов И.О. №23 Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если
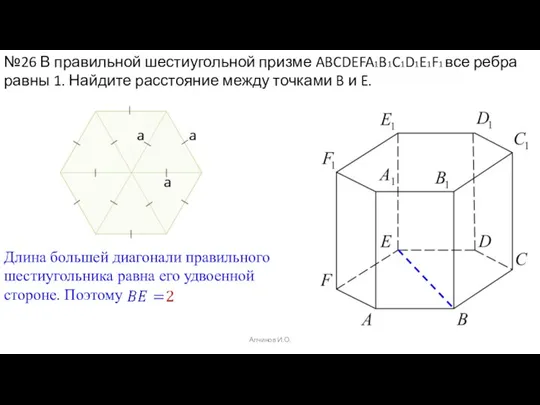
- 38. Алчинов И.О. №26 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками
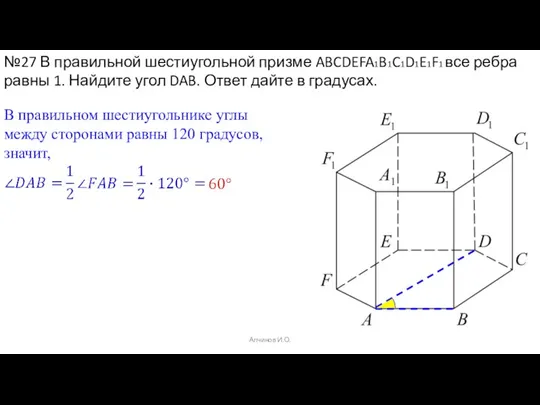
- 39. Алчинов И.О. №27 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ
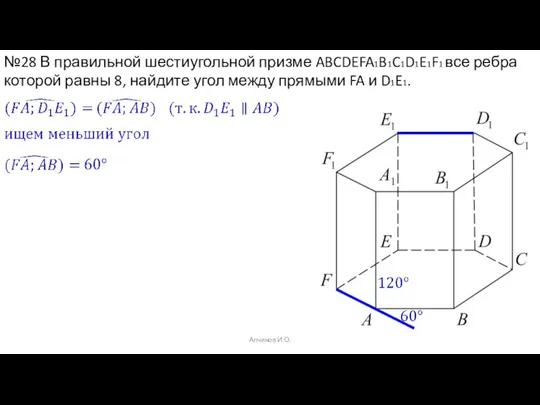
- 40. Алчинов И.О. №28 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра которой равны 8, найдите угол между
- 41. Алчинов И.О.
- 42. Алчинов И.О.
- 43. Алчинов И.О. №43 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками
- 44. Алчинов И.О.
- 45. Алчинов И.О. №45 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
- 46. Алчинов И.О. №46 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AС1С. Ответ
- 47. Алчинов И.О. Самостоятельная работа №3 1) Нахождение объёма части шестиугольной призмы 2) Нахождение угла между прямыми
- 48. Алчинов И.О. №29 В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в
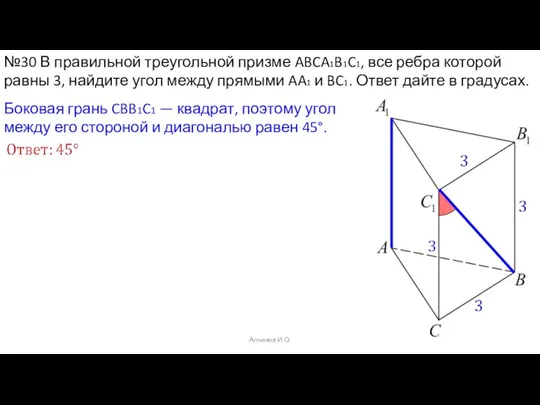
- 49. Алчинов И.О. №30 В правильной треугольной призме ABCA1B1C1, все ребра которой равны 3, найдите угол между
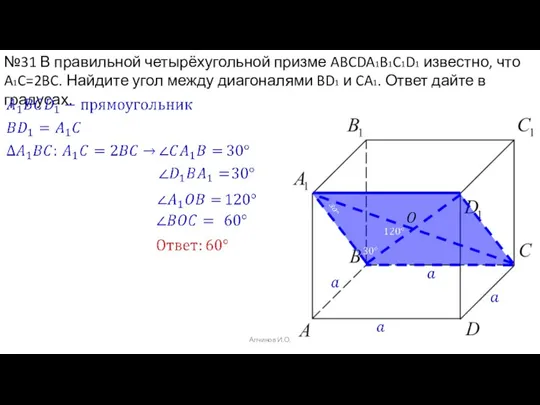
- 50. Алчинов И.О. №31 В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что A1C=2BC. Найдите угол между диагоналями BD1
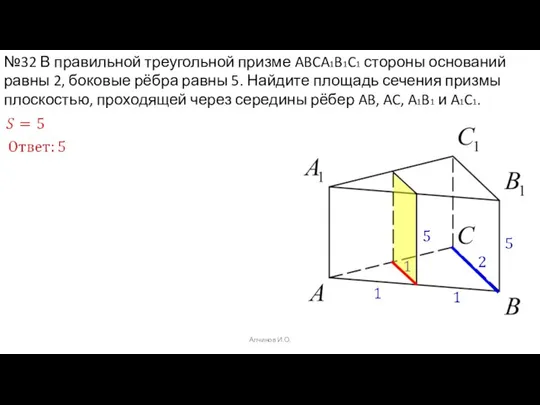
- 51. Алчинов И.О. №32 В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5.
- 52. Алчинов И.О. №33 В правильной четырёхугольной призме ABCDA1B1C1D1 ребро AA1 равно 15, а диагональ BD1 равна
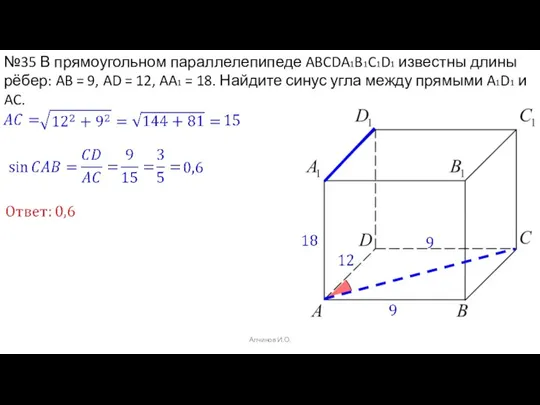
- 53. Алчинов И.О. №35 В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 9, AD = 12,
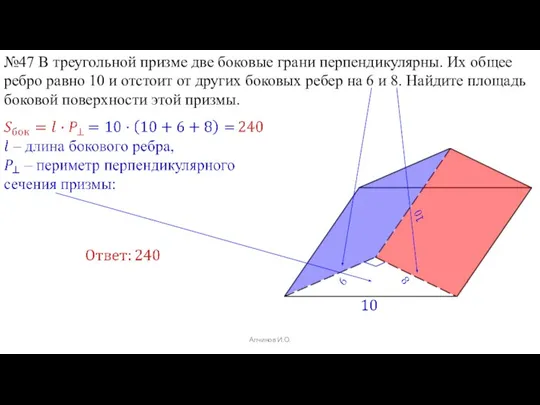
- 54. Алчинов И.О. №47 В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и
- 55. Алчинов И.О.
- 57. Скачать презентацию




































 Геометрический конструктор: Развивающая игра Танграм
Геометрический конструктор: Развивающая игра Танграм Модель частотно-регулируемого привода. (Тема 8)
Модель частотно-регулируемого привода. (Тема 8) Веселый счет. Викторина
Веселый счет. Викторина Производная сложной функции
Производная сложной функции Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые
Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые Мир в поверхности цилиндра
Мир в поверхности цилиндра Сложение чисел с разными знаками
Сложение чисел с разными знаками Многоугольники. Их формы
Многоугольники. Их формы Синус, косинус, тангенс и котангенс
Синус, косинус, тангенс и котангенс Развёртка куба
Развёртка куба Математика в танце
Математика в танце Линейное уравнение с одной переменной (7 класс)
Линейное уравнение с одной переменной (7 класс) Прямоугольник. Квадрат. Периметр многоугольника
Прямоугольник. Квадрат. Периметр многоугольника Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Понятие обыкновенной дроби. Упражнения
Понятие обыкновенной дроби. Упражнения Урок математики. 1 класс
Урок математики. 1 класс Ответы для самопроверки
Ответы для самопроверки Квадратный корень и его свойства
Квадратный корень и его свойства Математика в кинематографии
Математика в кинематографии Решение задач на готовых чертежах. Геометрия. 9 класс
Решение задач на готовых чертежах. Геометрия. 9 класс Презентация на тему Окружность и круг (5 класс)
Презентация на тему Окружность и круг (5 класс)  Работа над ошибками
Работа над ошибками Алгоритм вычисления площади с помощью палетки
Алгоритм вычисления площади с помощью палетки ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Презентация на тему Параллелепипед (9 класс)
Презентация на тему Параллелепипед (9 класс)  Алгоритм фронта волны
Алгоритм фронта волны Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия
Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия