Окружность. (Задача 18. Вариант 105)

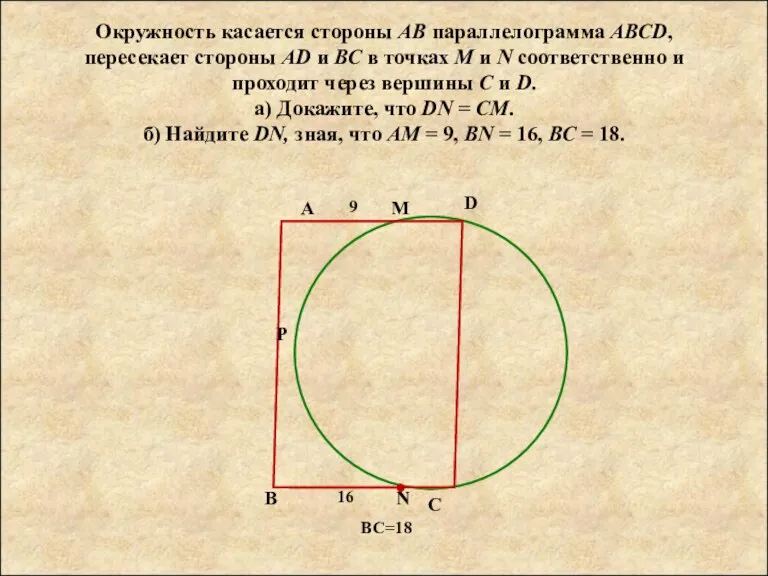
Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.

Доказательство:
ABCD – параллелограмм, ⇒
MD || NC ⇒ NMDC – трапеция.
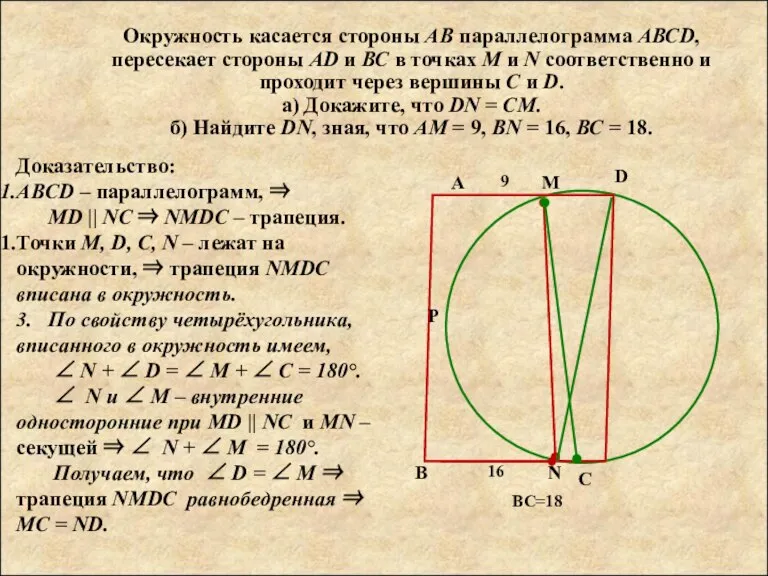
Точки M, D, C, N – лежат на окружности, ⇒ трапеция NMDC вписана в окружность.
3. По свойству четырёхугольника, вписанного в окружность имеем,
∠ N + ∠ D = ∠ M + ∠ C = 180°.
∠ N и ∠ M – внутренние односторонние при MD || NC и MN – секущей ⇒ ∠ N + ∠ M = 180°.
Получаем, что ∠ D = ∠ M ⇒ трапеция NMDC равнобедренная ⇒ МС = ND.
Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.

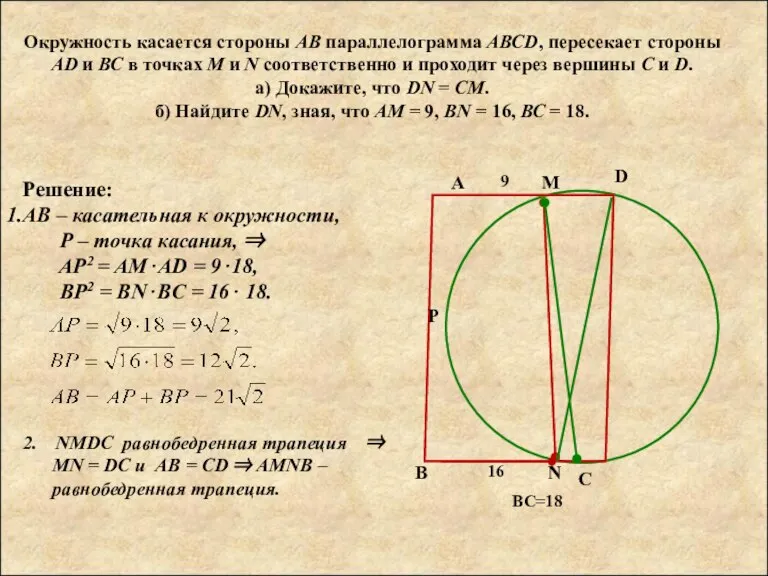
Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.
Решение:
АВ – касательная к окружности,
Р – точка касания, ⇒
AР2 = АМ⋅AD = 9⋅18,
ВР2 = BN⋅BC = 16⋅ 18.
2. NMDC равнобедренная трапеция ⇒ MN = DC и AB = CD ⇒ AMNB – равнобедренная трапеция.