Сфера, описанная вокруг многогранника

Определение: Многогранник называется вписанным в сферу (вписанным в шар), если все вершины многогранника принадлежат этой сфере.
Про сферу в этом случае говорят, что она описана около многогранника.

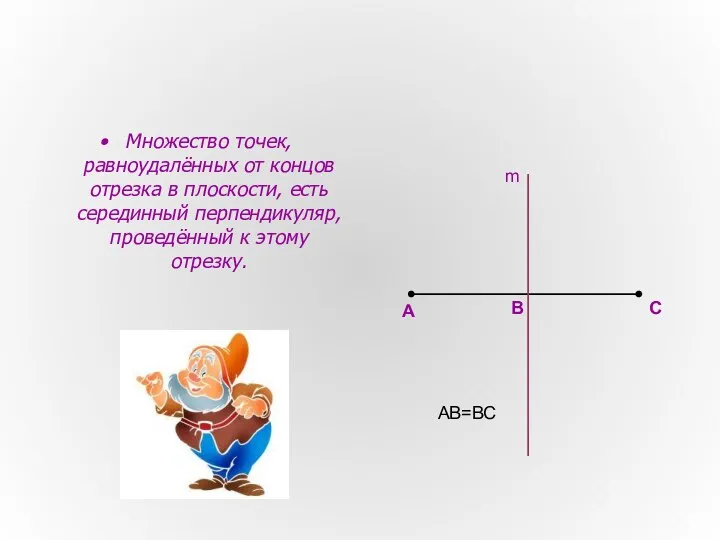
Множество точек, равноудалённых от концов отрезка в плоскости, есть серединный перпендикуляр, проведённый к этому отрезку.
А
В
С
АВ=ВС
m

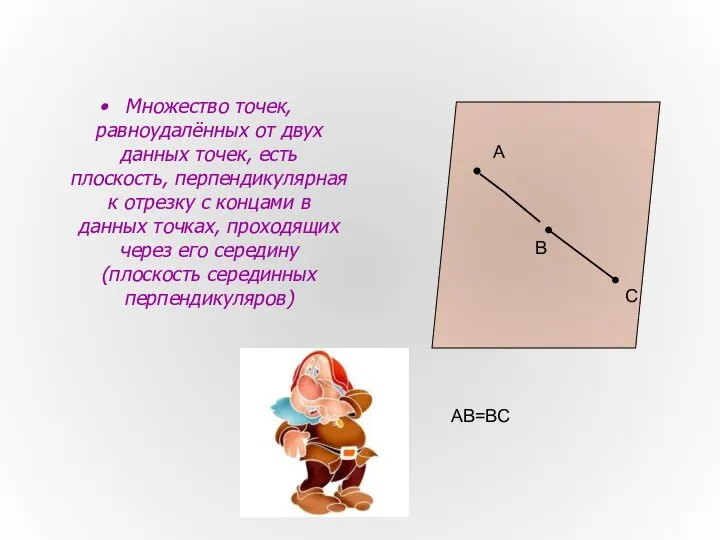
Множество точек, равноудалённых от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках, проходящих через его середину (плоскость серединных перпендикуляров)
А
В
С
АВ=ВС

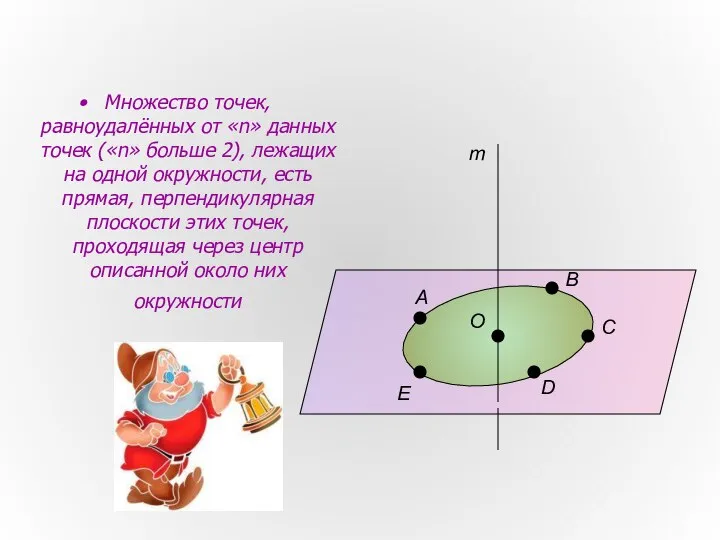
Множество точек, равноудалённых от «n» данных точек («n» больше 2), лежащих на одной окружности, есть прямая, перпендикулярная плоскости этих точек, проходящая через центр описанной около них окружности
А
В
С
D
E
O
m

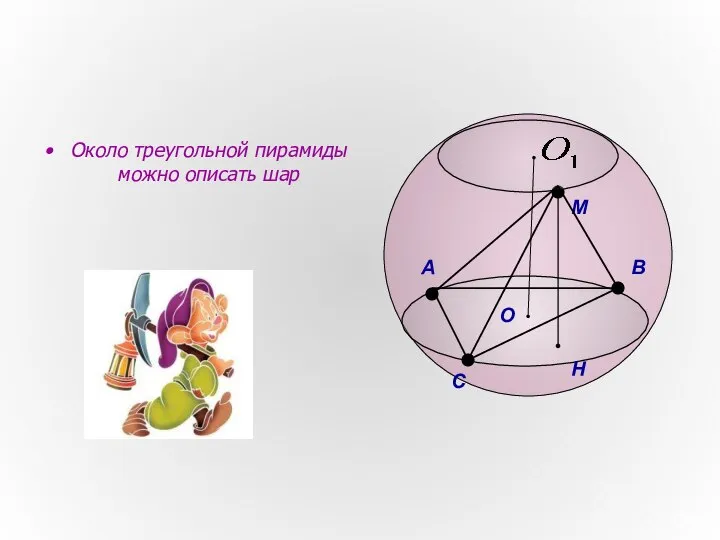
Около треугольной пирамиды можно описать шар
А
В
С
M
H
O

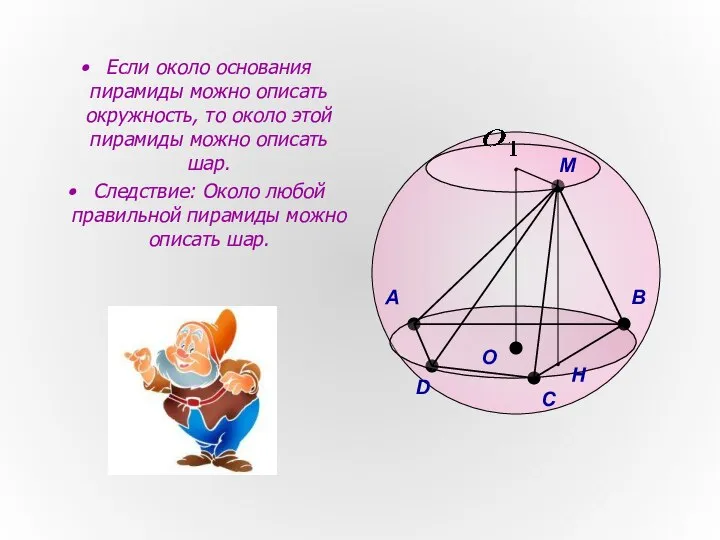
Если около основания пирамиды можно описать окружность, то около этой пирамиды можно описать шар.
Следствие: Около любой правильной пирамиды можно описать шар.
А
В
С
D
M
O
H

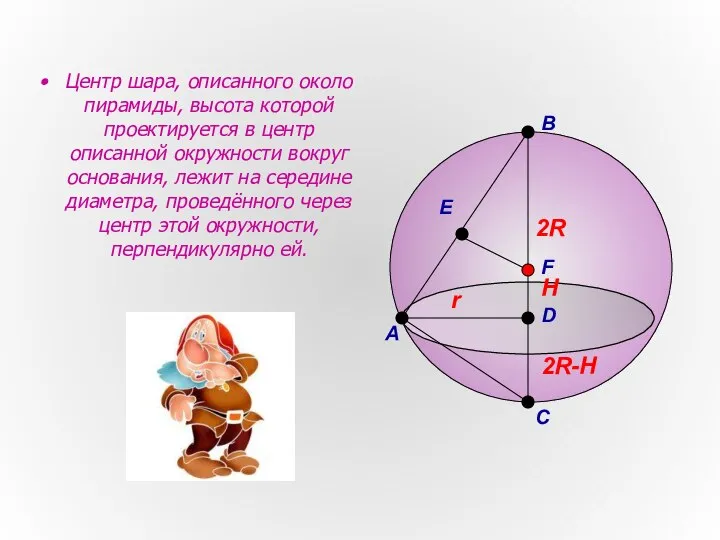
Центр шара, описанного около пирамиды, высота которой проектируется в центр описанной окружности вокруг основания, лежит на середине диаметра, проведённого через центр этой окружности, перпендикулярно ей.
А
В
С
D
Е
F
2R
H
r
2R-H

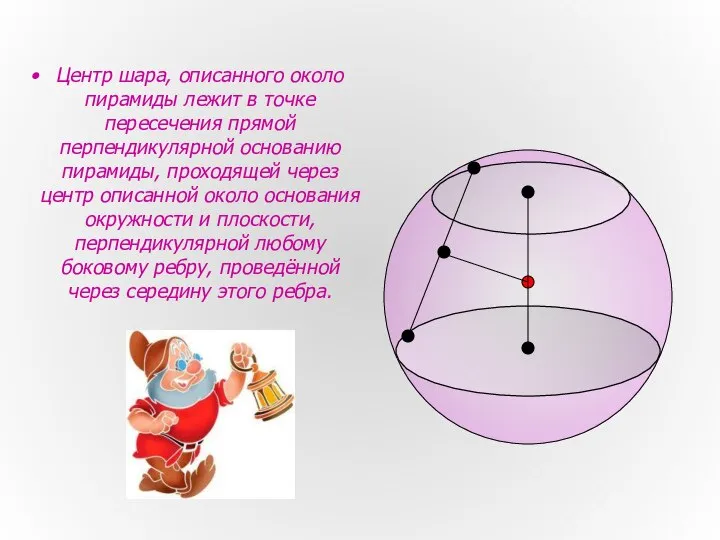
Центр шара, описанного около пирамиды лежит в точке пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведённой через середину этого ребра.