Содержание
- 2. Покажем криволинейный остряк в прижатом к рамному рельсу положении…
- 4. Для выполнения своих функций остряк должен перемещаться из прижатого положения в отведенное и наоборот…
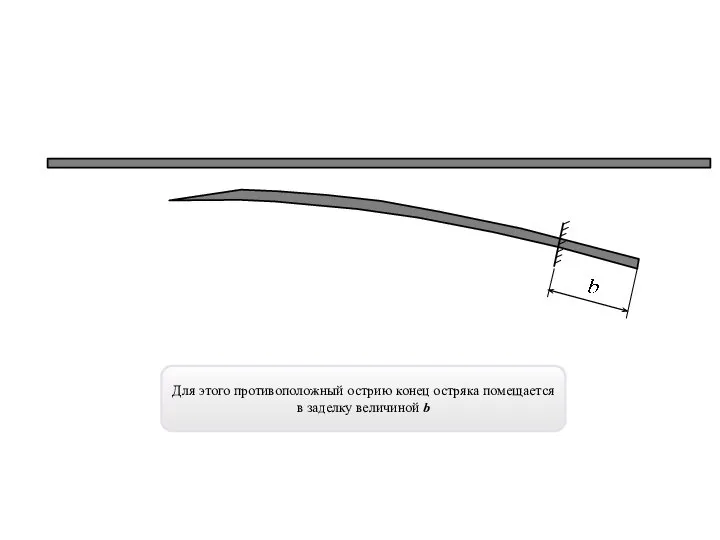
- 5. Для этого противоположный острию конец остряка помещается в заделку величиной b
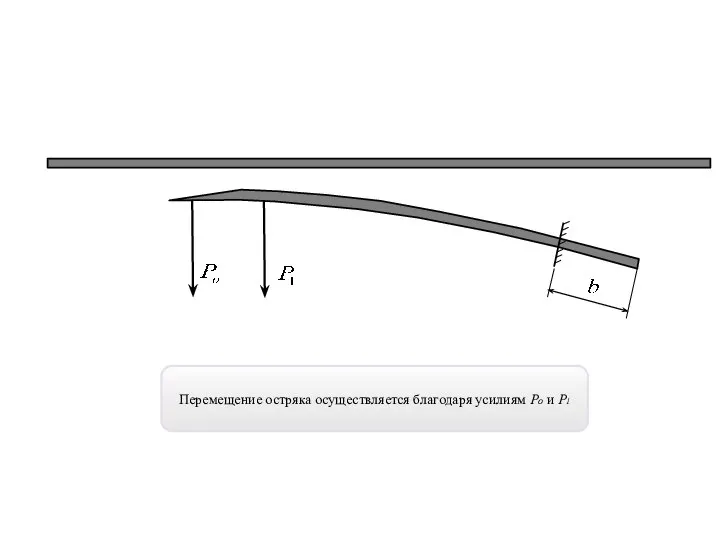
- 6. Перемещение остряка осуществляется благодаря усилиям Ро и Р1
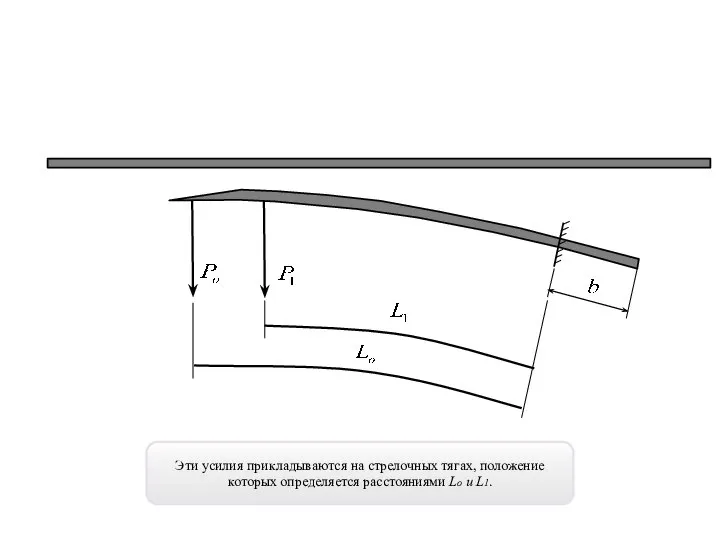
- 7. Эти усилия прикладываются на стрелочных тягах, положение которых определяется расстояниями Lo и L1.
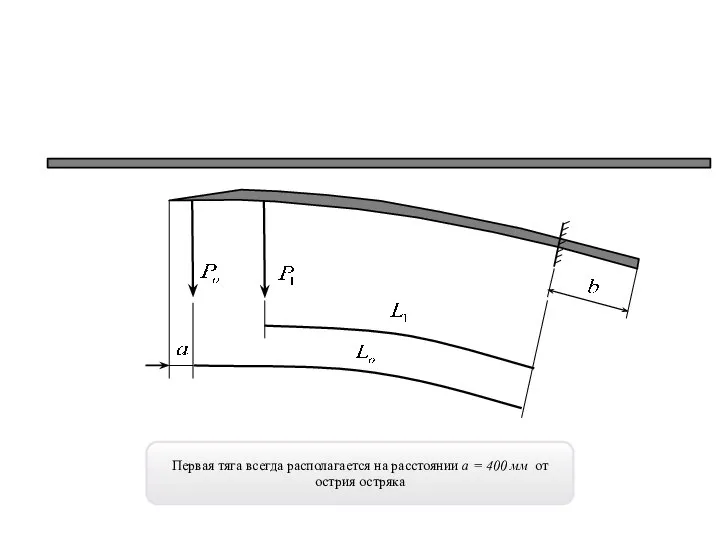
- 8. Первая тяга всегда располагается на расстоянии а = 400 мм от острия остряка
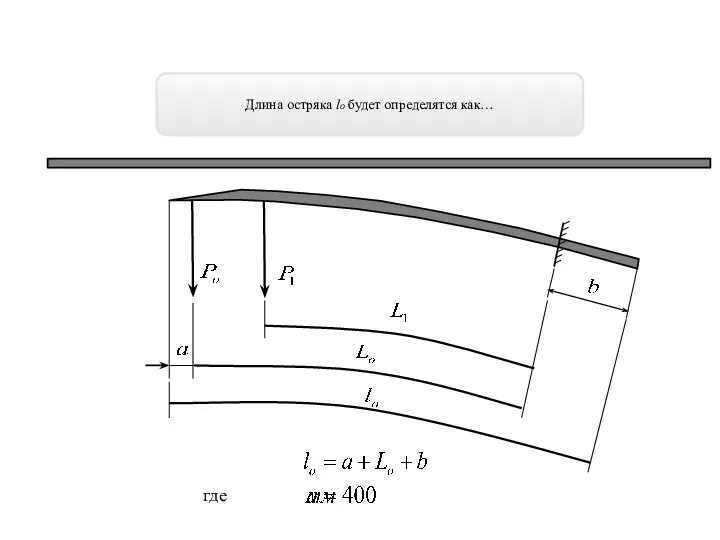
- 9. Длина остряка lo будет определятся как… где
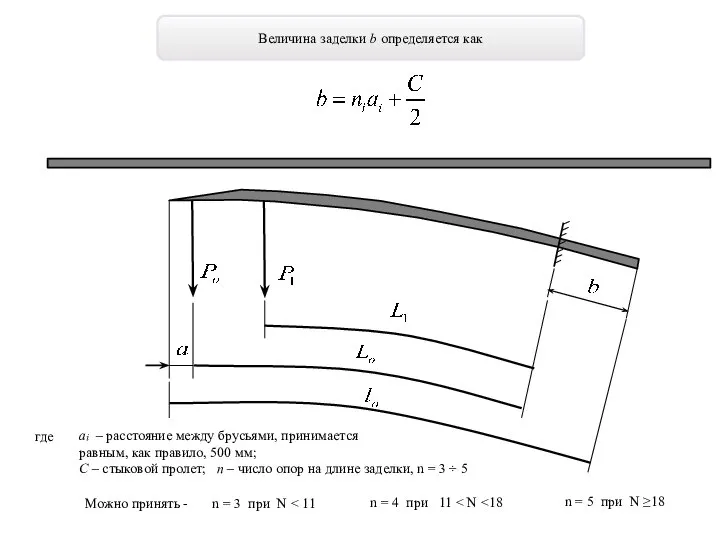
- 10. Величина заделки b определяется как где ai – расстояние между брусьями, принимается равным, как правило, 500
- 11. Длина остряков и тяговых усилий сводится к подбору минимальной длины остряка lo . При этом должны
- 12. Допускаемые значения |t| принимаются равными - для прямого направления - для бокового направления приняв kt =
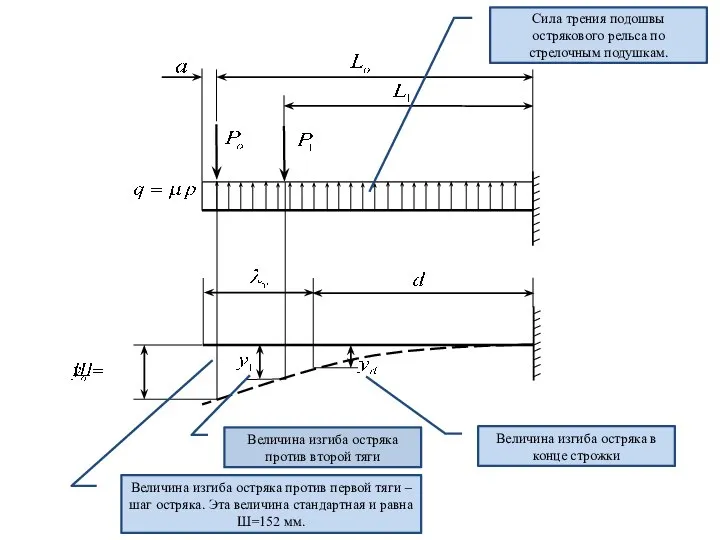
- 13. Для определения длины остряков и тяговых усилий принимают следующую расчетную схему
- 14. Величина изгиба остряка против первой тяги – шаг остряка. Эта величина стандартная и равна Ш=152 мм.
- 15. Величина изгиба остряка против второй тяги y1 принимается на 5 ÷ 15 мм больше, чем т.е.
- 16. Для решения используют методы строительной механики. Методика расчета подробно изложена в п.3.1.5 учебного пособия…
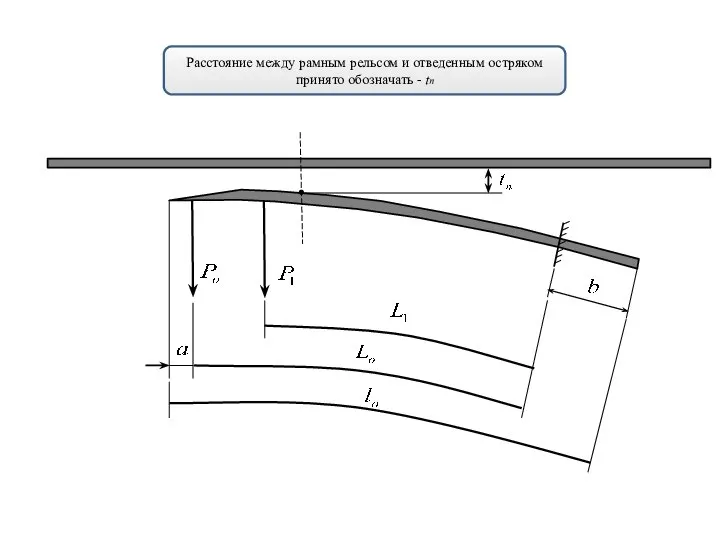
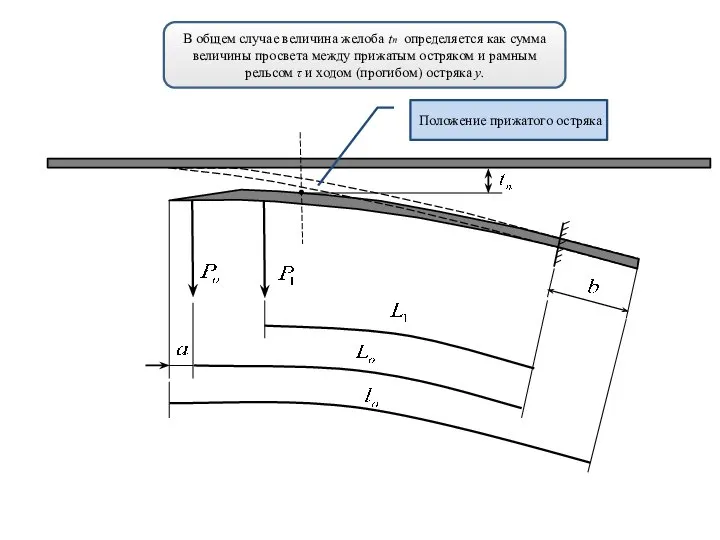
- 17. Расстояние между рамным рельсом и отведенным остряком принято обозначать - tп
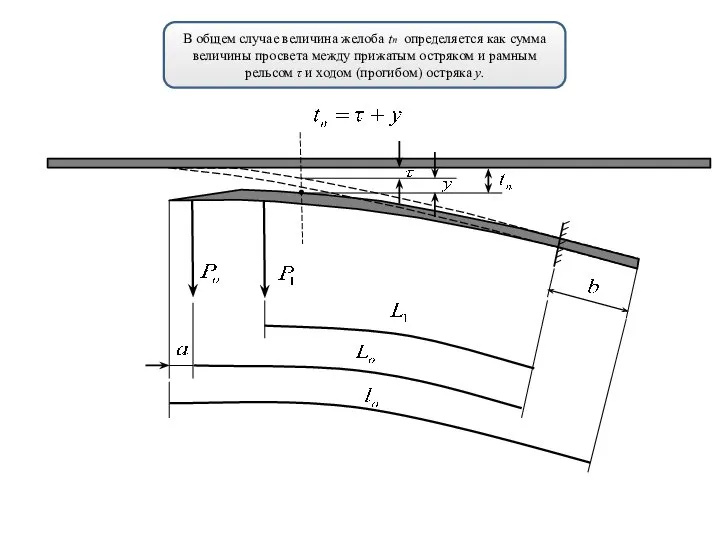
- 18. В общем случае величина желоба tп определяется как сумма величины просвета между прижатым остряком и рамным
- 19. В общем случае величина желоба tп определяется как сумма величины просвета между прижатым остряком и рамным
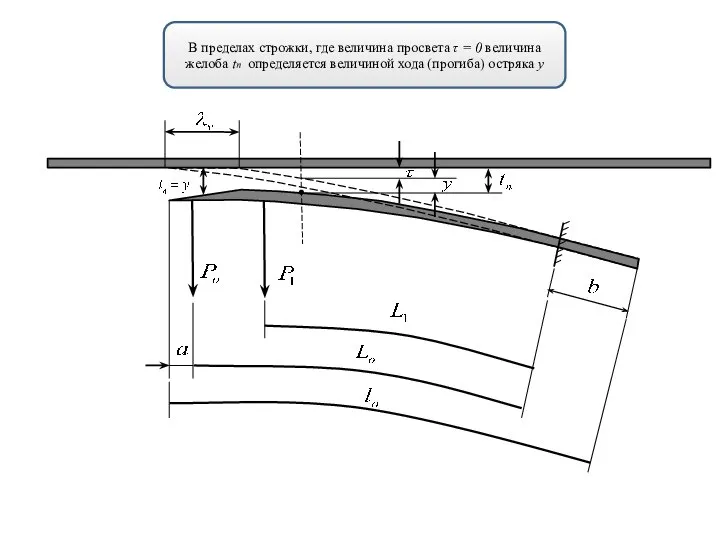
- 20. В пределах строжки, где величина просвета τ = 0 величина желоба tп определяется величиной хода (прогиба)
- 21. Последовательность расчета
- 22. 1. При расчете сначала проверяется возможность перевода остряка с помощью одной тяги. В этом случае задаются
- 23. Обычно в этом случае при существующих параметрах проектирования длина остряка получается слишком большой, что не допустимо,
- 25. Скачать презентацию










 Сумма углов треугольника
Сумма углов треугольника Применение свойств квадратичной функции при решении задач
Применение свойств квадратичной функции при решении задач Практикумы по задачам на готовых чертежах
Практикумы по задачам на готовых чертежах Векторы в координатах
Векторы в координатах Комбинированный урок
Комбинированный урок Математическая логика
Математическая логика Формулы сокращенного умножения
Формулы сокращенного умножения Произведение вектора на число
Произведение вектора на число Преобразование функций и действия над ними
Преобразование функций и действия над ними Диаграммы. Matplotlib ч. 2
Диаграммы. Matplotlib ч. 2 Сдвиг графика функции у=ах2 вдоль осей координат. Этапы построения графиков функции в Microsoft Excel
Сдвиг графика функции у=ах2 вдоль осей координат. Этапы построения графиков функции в Microsoft Excel Мнимые числа. Определение комплексных чисел
Мнимые числа. Определение комплексных чисел Практика. Дискретная математика
Практика. Дискретная математика Основы метрологического обеспечения
Основы метрологического обеспечения Прямая на плоскости
Прямая на плоскости Окружность. Элементы окружности. Формулы
Окружность. Элементы окружности. Формулы Промежутки возрастания, убывания, знакопостоянства и нули функции
Промежутки возрастания, убывания, знакопостоянства и нули функции Признаки подобия треугольников
Признаки подобия треугольников Исаак Ньютон
Исаак Ньютон Криволинейные интегралы. Теория поля
Криволинейные интегралы. Теория поля Закрепление таблицы умножения и деления
Закрепление таблицы умножения и деления Многогранный угол. Трёхгранный угол
Многогранный угол. Трёхгранный угол Теорема Пифагора
Теорема Пифагора Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Движение. Центральная, осевая и зеркальная симметрии. Параллельный перенос
Движение. Центральная, осевая и зеркальная симметрии. Параллельный перенос Элементы теории вероятности и математической статистики
Элементы теории вероятности и математической статистики Линейные пространства и линейные операторы. Лекция 6
Линейные пространства и линейные операторы. Лекция 6 Алгебраические уравнения
Алгебраические уравнения