Площадь сферы

поговорим о формуле для вычисления площади поверхности сферы
узнаем, какой многогранник называется описанным около сферы
решим несколько задач на применение формулы для вычисления площади сферы
Сегодня на уроке:

Определение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Данная точка называется центром сферы.
Данное расстояние – радиусом сферы.
радиус

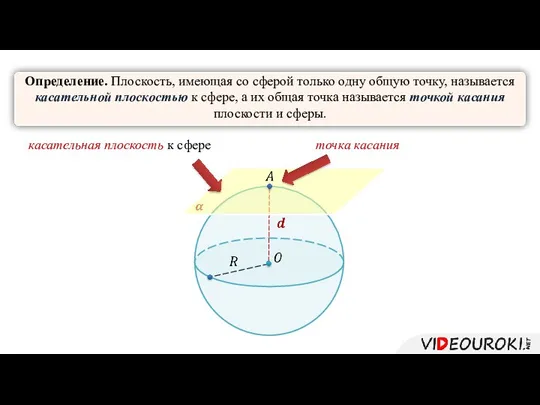
Определение. Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
касательная плоскость к сфере
точка касания

Свойство касательной плоскости к сфере.
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Признак касательной плоскости к сфере.
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

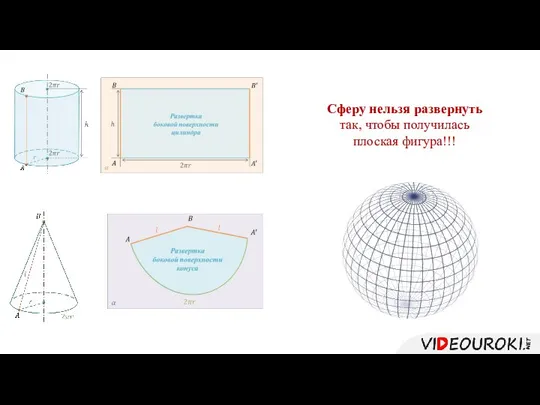
Сферу нельзя развернуть так, чтобы получилась плоская фигура!!!

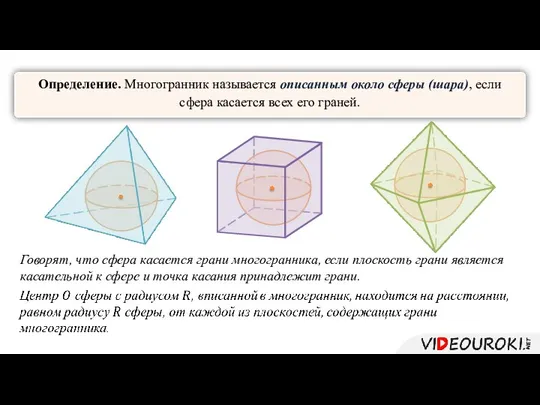
Определение. Многогранник называется описанным около сферы (шара), если сфера касается всех его граней.
Говорят, что сфера касается грани многогранника, если плоскость грани является касательной к сфере и точка касания принадлежит грани.

Рассмотрим последовательность описанных около данной сферы многогранников.
Наибольшим размером грани мы будем называть наибольшее расстояние между двумя точками грани.
Представим себе, что количество граней многогранника стало бесконечно много.
Тогда площадь поверхности многогранника будет приближаться к площади сферы.
За площадь сферы можно принять предел последовательности площадей поверхностей этих многогранников при стремлении к нулю наибольшего размера каждой грани.

Решение.

Решение.

Решение.

Решение.