Содержание
- 2. Концентрация внимания Концентрация внимания равна N. N = (число верно указанных чисел) x 0,125 x 100%
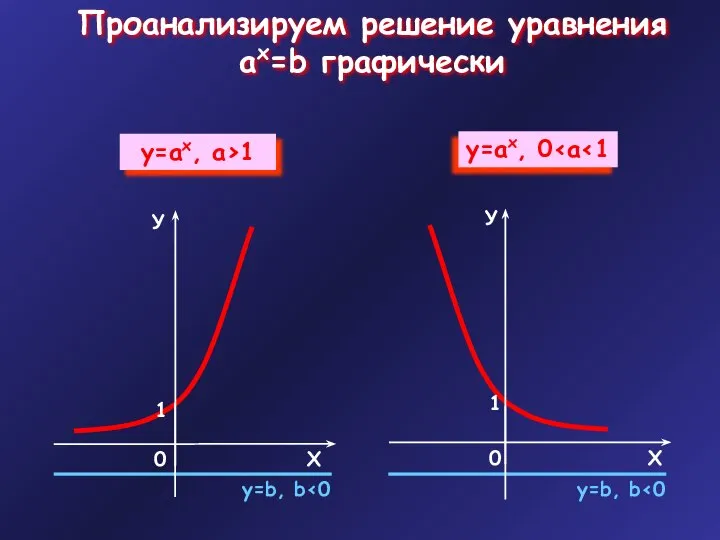
- 4. Проанализируем решение уравнения ax=b графически у=b, b у=b, b
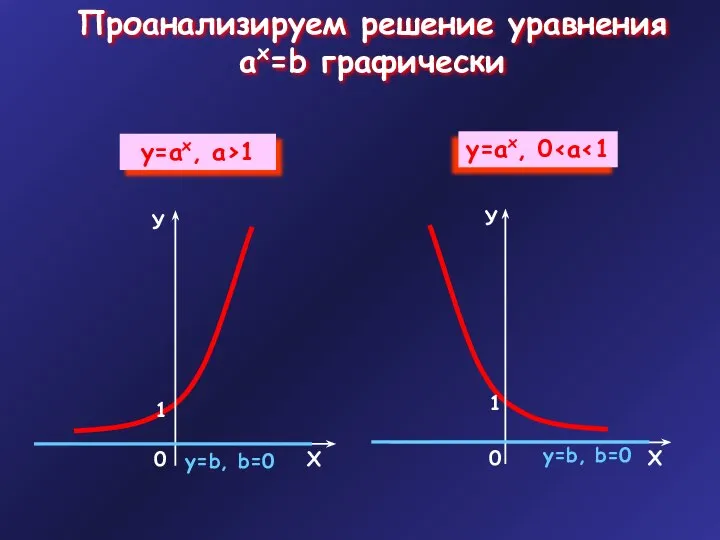
- 5. Проанализируем решение уравнения ax=b графически у=b, b=0 у=b, b=0
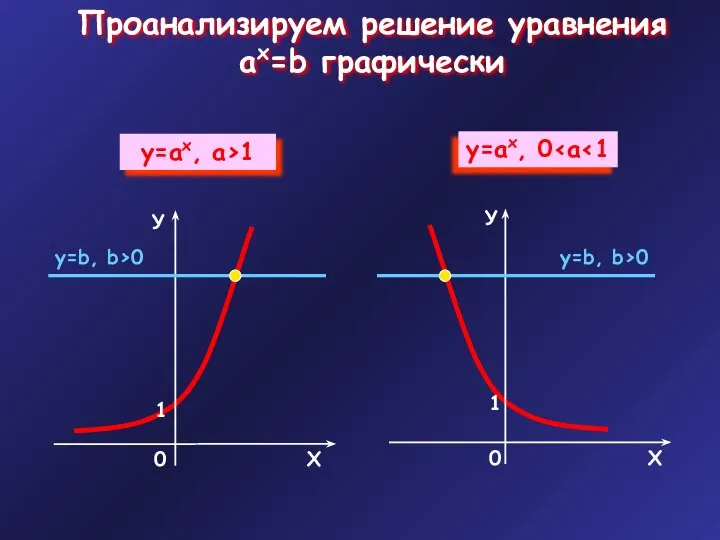
- 6. Проанализируем решение уравнения ax=b графически у=b, b>0 у=b, b>0
- 7. Уравнение ax=b корней не имеет Уравнение ax=b имеет единственное решение x=logab b>0 b≤0 Вывод:
- 8. Пример:
- 9. Во многих случаях решение показательных уравнений после надлежащих преобразований сводится к решению простейших показательных уравнений. При
- 10. ОТВЕТ: -5 ; 1.
- 11. ОТВЕТ: 1.
- 13. ПРИМЕР Показательные уравнения, сводящиеся к квадратным уравнениям. ТИП Вернемся к переменной Х . ОТВЕТ:
- 15. ОТВЕТ:
- 17. . Вернёмся к переменной x ОТВЕТ: 0 ; 1
- 18. Вернёмся к переменной x ОТВЕТ: 0 ; 1.
- 20. ОТВЕТ: Вернёмся к переменной x
- 22. Введём функции и . Функция убывает на R, как сумма убывающих на R. Функция постоянна на
- 23. Легко определить и проверить, что х=3 - корень данного уравнения. Покажем, что других корней уравнение иметь
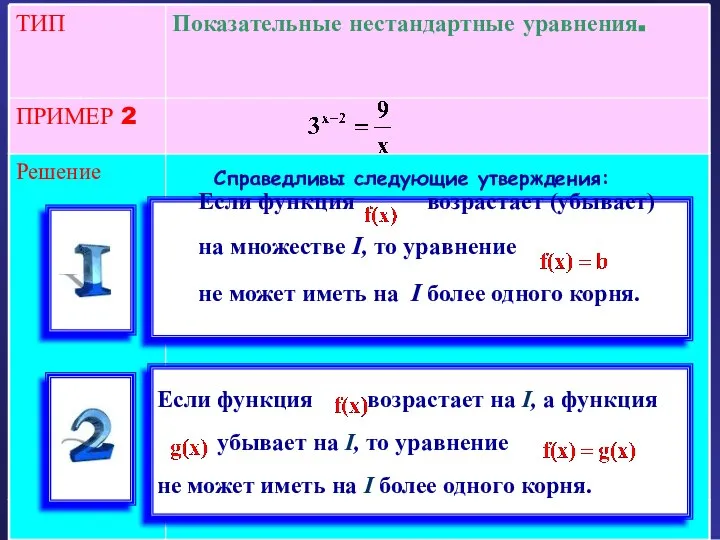
- 24. Решение ПРИМЕР 2 Показательные нестандартные уравнения. ТИП Справедливы следующие утверждения: Если функция возрастает (убывает) на множестве
- 25. ОТВЕТ: 3 Введём функции и . Показательная функция ( ) возрастает на R. Функция (обратная пропорциональность)
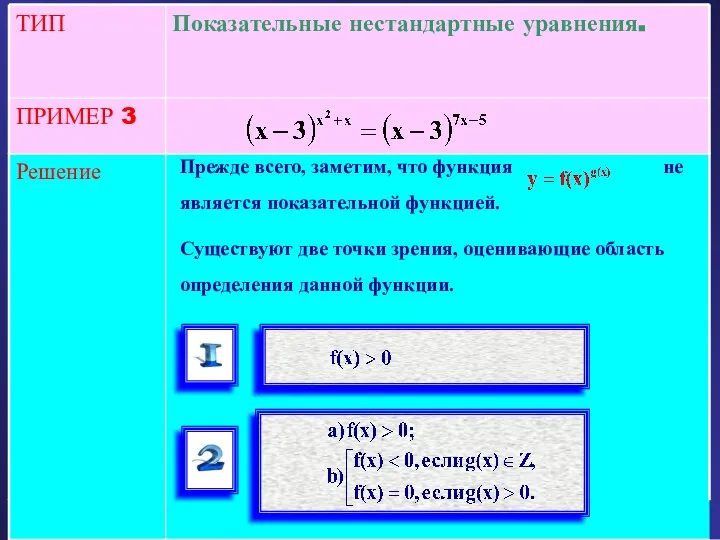
- 26. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Прежде всего, заметим, что функция не является показательной функцией.
- 27. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Решим данное уравнение, придерживаясь второй точки зрения. Вначале проверим,
- 28. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Проверка показала, что x=3 является корнем уравнения. Проверка показала,
- 29. Решение ПРИМЕР 3 Показательные нестандартные уравнения. ТИП Теперь установим, какие из корней уравнения удовлетворяют исходному уравнению.
- 30. ОТВЕТ: 5 ; 4 ; 3 ; 1 Проверка показала, что х=5 является корнем уравнения. Замечание:
- 31. Домашнее задание:
- 33. Скачать презентацию

























 Введение в биоинформатику. Лекция 9
Введение в биоинформатику. Лекция 9 Числото шест
Числото шест Занятие 1_2022
Занятие 1_2022 Таблица умножения и деления с числом 7
Таблица умножения и деления с числом 7 Решение задач на нахождение зависимости между величинами используя графики
Решение задач на нахождение зависимости между величинами используя графики Начальные геометрические сведения
Начальные геометрические сведения Презентация на тему Пентамино
Презентация на тему Пентамино  Деление квадрата на 4 равные части
Деление квадрата на 4 равные части Проверка деления
Проверка деления Признаки делимости на 11
Признаки делимости на 11 Пирамиды. Объём пирамиды
Пирамиды. Объём пирамиды Математика. Вспоминаем, повторяем
Математика. Вспоминаем, повторяем Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Объём цилиндра. Решение задач
Объём цилиндра. Решение задач Геометрия. Построение
Геометрия. Построение Круги Эйлера в решении задач
Круги Эйлера в решении задач Логарифмические уравнения. Обобщающий урок
Логарифмические уравнения. Обобщающий урок Степень числа
Степень числа Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Нахождение числа по его дроби
Нахождение числа по его дроби Матрицы и действия на матрицами
Матрицы и действия на матрицами Скрипт параллелограм
Скрипт параллелограм Площадь треугольника
Площадь треугольника Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Повторение. Решение уравнений
Повторение. Решение уравнений Презентация на тему Математический супертест
Презентация на тему Математический супертест  Нахождение коэффициентов квадратичной функции по графику
Нахождение коэффициентов квадратичной функции по графику Рубежный (итоговый) контроль по математике в 6-х классах образовательных учреждений г.Москвы апрель 2007 года
Рубежный (итоговый) контроль по математике в 6-х классах образовательных учреждений г.Москвы апрель 2007 года