Содержание
- 2. Цель: изучение геометрического смысла производной функции
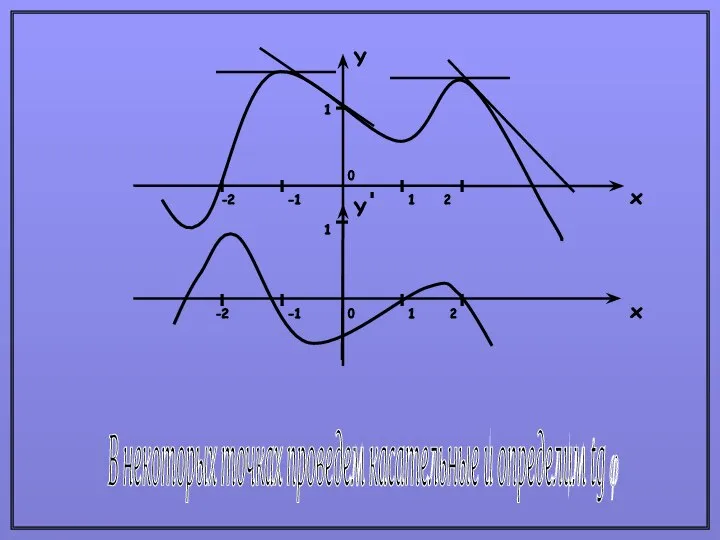
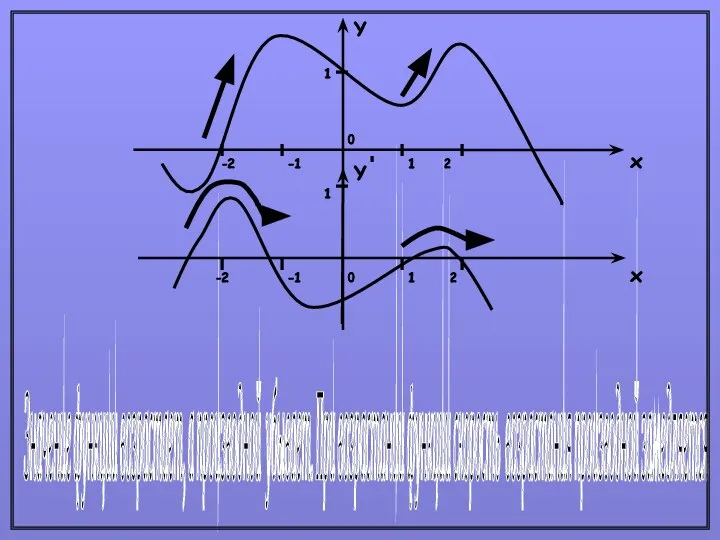
- 3. В некоторых точках проведем касательные и определим tg φ Y x x Y 1 -1 2
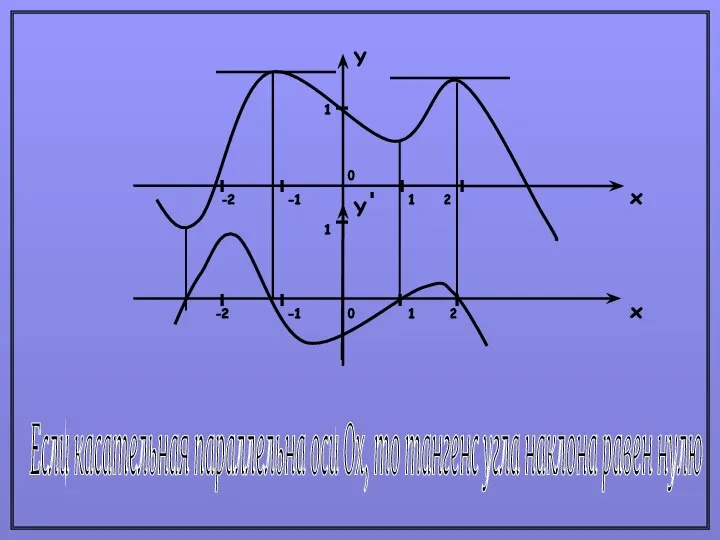
- 4. Если касательная параллельна оси Ох, то тангенс угла наклона равен нулю Y x x Y 1
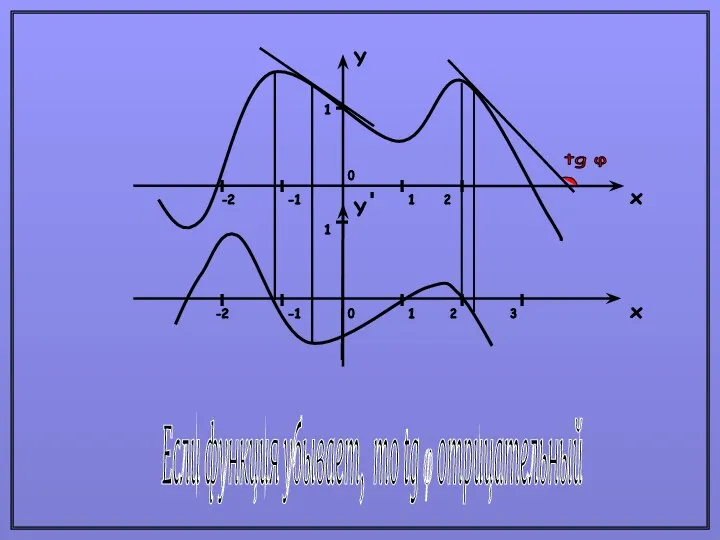
- 5. Если функция убывает, то tg φ отрицательный Y x x Y 1 -1 2 -2 0
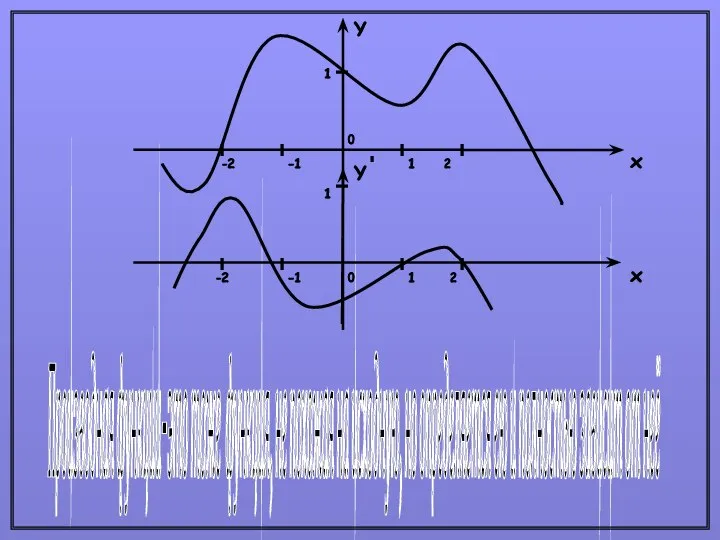
- 6. При построении производной видны "необычные вещи"
- 7. Производная функции-это тоже функция, не похожая на исходную, но определяется ею и полностью зависит от неё
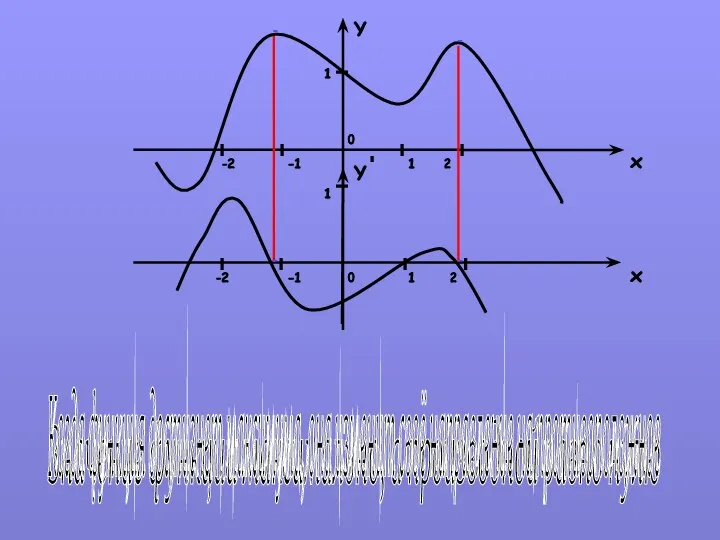
- 8. Значение функции возрастает, а производной убывает. При возрастании функции скорость возрастания производной замедляется Y x x
- 9. Значение функции максимально, а производной равно нулю Y x x Y 1 -1 2 -2 0
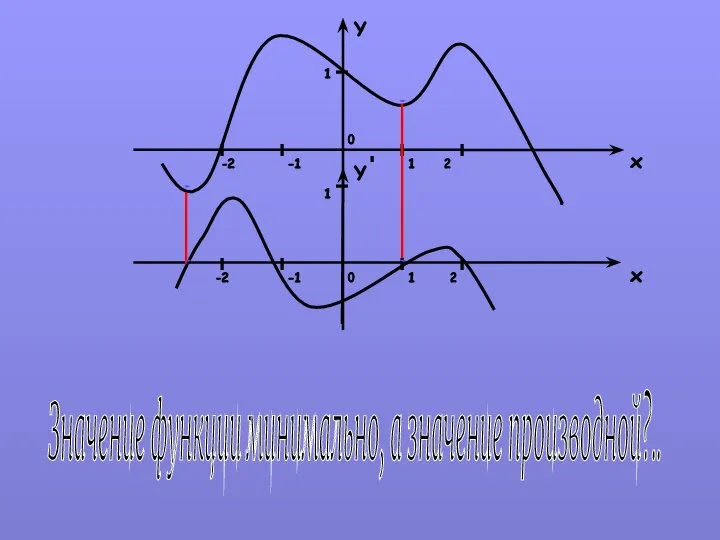
- 10. Значение функции минимально, а значение производной?.. Y x x Y 1 -1 2 -2 0 0
- 12. Скачать презентацию


 Признаки параллельности прямых
Признаки параллельности прямых Сокращение дробей. Самоанализ
Сокращение дробей. Самоанализ Математический тренажёр Бабушкины примеры
Математический тренажёр Бабушкины примеры Математика в парикмахерском искусстве
Математика в парикмахерском искусстве Пропорция. Пропорциональность и обратная пропорциональность
Пропорция. Пропорциональность и обратная пропорциональность Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Презентация на тему Понятие движения (9 класс)
Презентация на тему Понятие движения (9 класс)  Число и цифра 0 (1 класс)
Число и цифра 0 (1 класс) Определение медианы
Определение медианы Методы решения логических задач
Методы решения логических задач Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Сфера. Окружность и круг
Сфера. Окружность и круг Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся
Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника
Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника Действия с алгебраическими дробями
Действия с алгебраическими дробями Презентация на тему Прототипы В12. Задачи на проценты
Презентация на тему Прототипы В12. Задачи на проценты  Задача на движение
Задача на движение Уравнение (урок математики, 5 класс)
Уравнение (урок математики, 5 класс)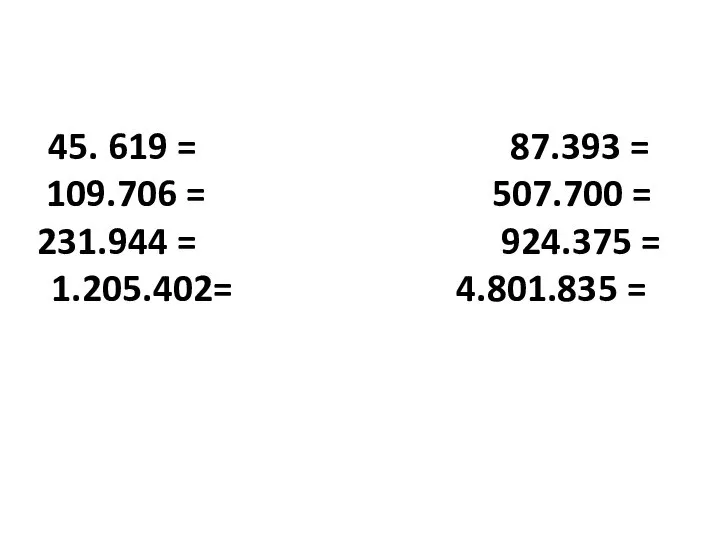 Разряды чисел
Разряды чисел Параллельность плоскостей
Параллельность плоскостей Неопределенный интеграл. Методы интегрирования
Неопределенный интеграл. Методы интегрирования Серединный перпендикуляр
Серединный перпендикуляр Транспортная задача. Методы нахождения начального решения транспортной задачи
Транспортная задача. Методы нахождения начального решения транспортной задачи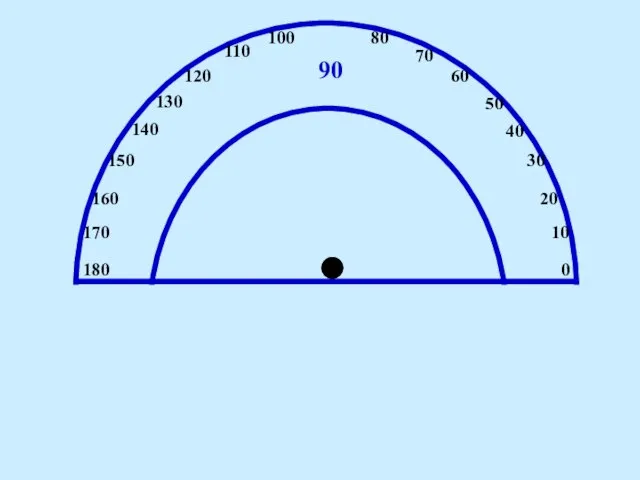 Презентация на тему Транспортир
Презентация на тему Транспортир  Деление с остатком. 4 класс
Деление с остатком. 4 класс