Слайд 2Размещением из n элементов
по k (k ≤ n) называется
любое множество

,состоящее из k элементов, взятых в
определенном порядке из данных n элементов.
Слайд 3Формула для вычисления размещении из n элементов по k
Замечание: Когда n =

k, получается
Будем считать по определению 0! = 1,
то есть
Слайд 4Переходим к рассмотрению задач

Слайд 5Из 20 учеников нашего класса необходимо выбрать командира класса и его заместителя.

Сколькими способами это можно сделать?
Слайд 6Решение:
20!
(20-2)!
Ответ: 380 способов

Слайд 7Сколько различных двухзначных чисел можно записать с помощью цифр 1,2,3,4, если каждую

цифру в двухзначном числе можно использовать лишь один раз?
Слайд 8Решение:
4!
(2-2)!
Ответ: 12 чисел

Слайд 9Учащиеся нашего класса изучают 15 предметов. Сколькими способами можно
составить расписание на

1 день, чтобы в
нем было 6 различных предметов?
Слайд 10Решение:
15!
(15-6)!
Ответ: 3603600 способов

Слайд 11Сколькими способами 6 учеников, сдающих экзамен, могут занять места в аудитории, в

которой стоит 20 одноместных столов?
Слайд 12Решение:
20!
(20-6)!
Ответ: 27907200 способов

Слайд 13Работу выполнили:
Талипова Руфина
Сочнева Аня
Хасаншина Ариель
Марьин Сергей
Романова Даша
Тарасов Женя













 Комплексные числа и действия над ними
Комплексные числа и действия над ними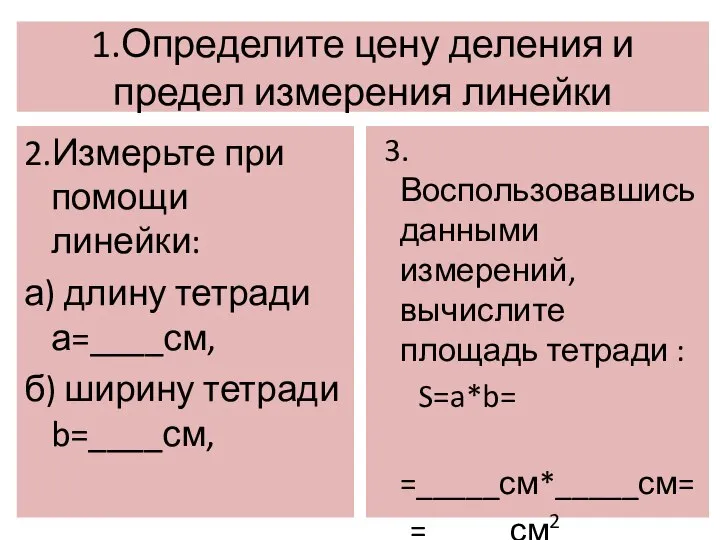 Цена деления и предел измерения линейки
Цена деления и предел измерения линейки Состав чисел
Состав чисел Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу
Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу Реши уравнения
Реши уравнения Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Треугольники
Треугольники Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Решение уравнений с одной переменной
Решение уравнений с одной переменной Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Признаки параллельности прямых
Признаки параллельности прямых Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Математика. Числа до 20
Математика. Числа до 20 Какой функции соответствует график
Какой функции соответствует график Контрольная работа
Контрольная работа Теория антагонистических игр. Задачи для выполнения
Теория антагонистических игр. Задачи для выполнения Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Задачи на перебор вариантов
Задачи на перебор вариантов Решение тригонометрических уравнений
Решение тригонометрических уравнений Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора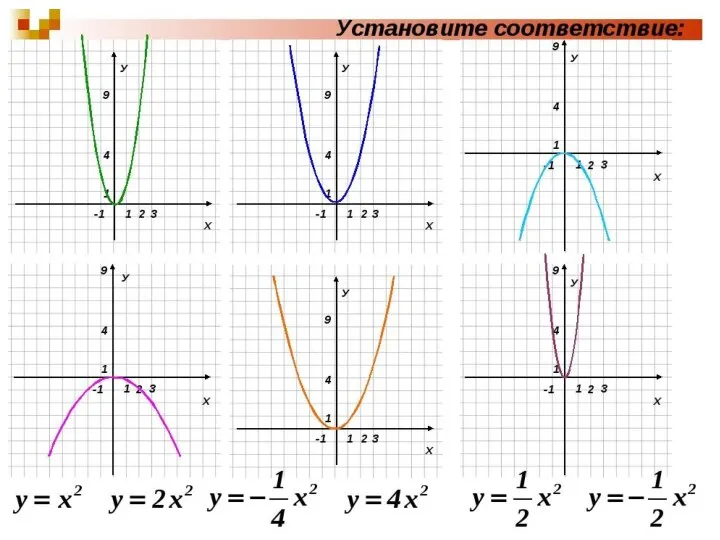 Графики функций
Графики функций Результант. Литература
Результант. Литература Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла