Третий признак равенства треугольников. 7 класс

Цели:
изучить третий признак равенства треугольников, выработать навыки
использования их при решении задач. систематизировать, расширить и углубить знания учащихся о треугольнике, закрепить навыки и умения при решении задач, используя определения и теоремы по данной теме.

Ход урока
1.Организационный момент
2.Повторение
3.Изучение нового материала
4.Закрепление из материала
5.Домашнее задание

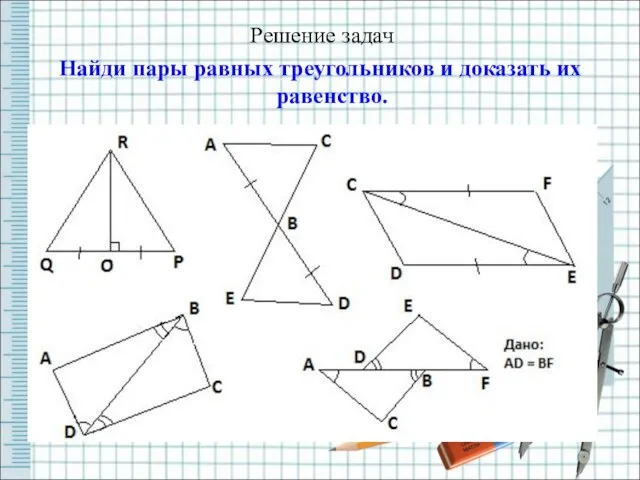
Решение задач
Найди пары равных треугольников и доказать их равенство.

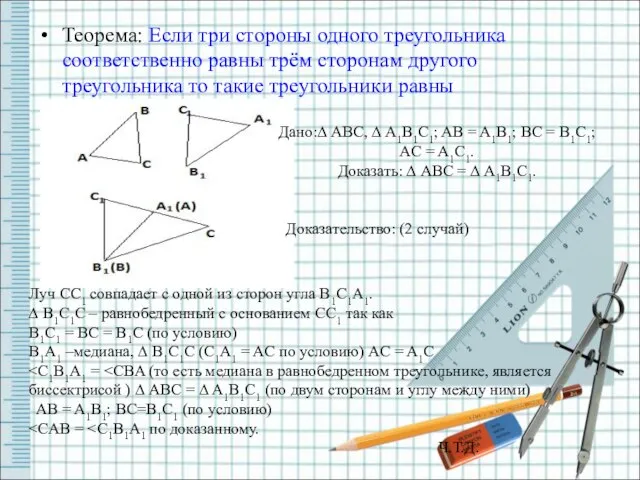
Теорема: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника то такие треугольники равны
Дано:∆ ABC, ∆ A1B1C1; AB = A1B1; BC = B1C1;
AC = A1C1.
Доказать: ∆ ABC = ∆ A1B1C1.
Доказательство: (2 случай)
Луч CC1 совпадает с одной из сторон угла B1C1A1.
∆ B1C1C – равнобедренный с основанием CC1 так как
B1C1 = BC = B1C (по условию)
B1A1 –медиана, ∆ B1C1C (C1A1 = AC по условию) AC = A1C
AB = A1B1; BC=B1C1 (по условию)
Ч.Т.Д.

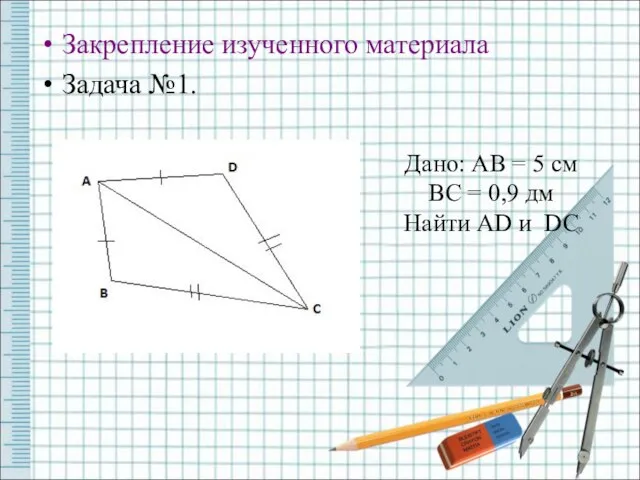
Закрепление изученного материала
Задача №1.
Дано: AB = 5 см
BC = 0,9 дм
Найти AD и DC

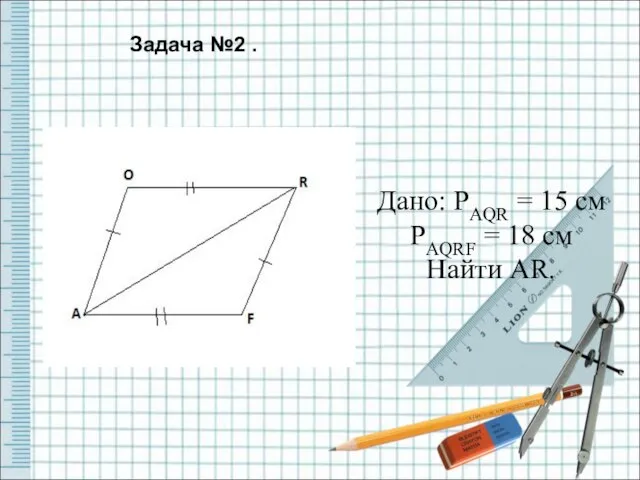
Дано: PAQR = 15 см
PAQRF = 18 см
Найти AR.
Задача №2 .

Стороны одного треугольника равны 30 см, 40 см и 0,5 м, а другого – 30 см, 40см и 5 дм. Равны ли эти треугольники?
Задача №3.

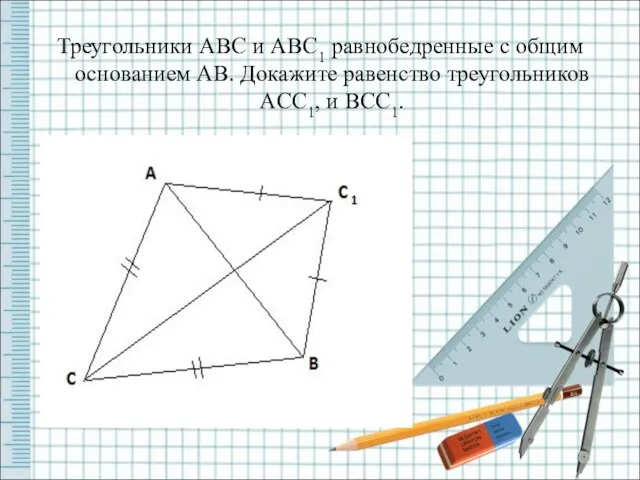
Треугольники ABC и ABC1 равнобедренные с общим основанием AB. Докажите равенство треугольников ACC1, и BCC1.

Решение:
Рассмотрим ∆ACC1 и ∆ BCC1,
AC = BC1 ,так как ∆ ABC1 – равнобедренный
AC = CB ,так как треугольник ABC – равнобедренный сторона CC1 – общая у ∆ ACC1 и ∆ BCC1 , следовательно ∆ ACC1 = ∆ BCC1 по трём сторонам.
Ч.Т.Д