Содержание
- 2. Должны узнать - Что называется углом между прямой и плоскостью? - Как построить угол между прямой
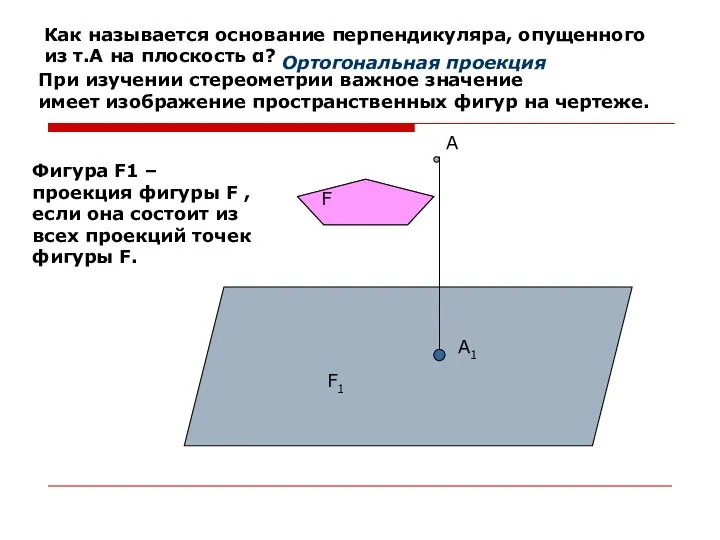
- 3. А А1 Как называется основание перпендикуляра, опущенного из т.А на плоскость α? Ортогональная проекция При изучении
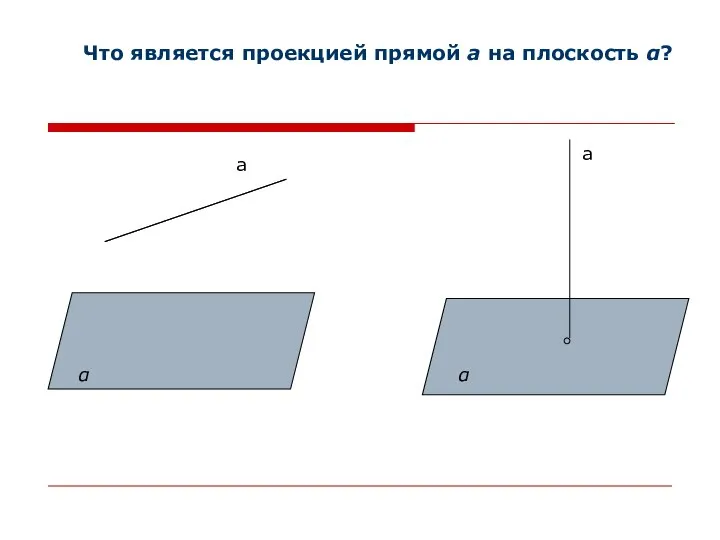
- 4. a a Что является проекцией прямой а на плоскость α? α α
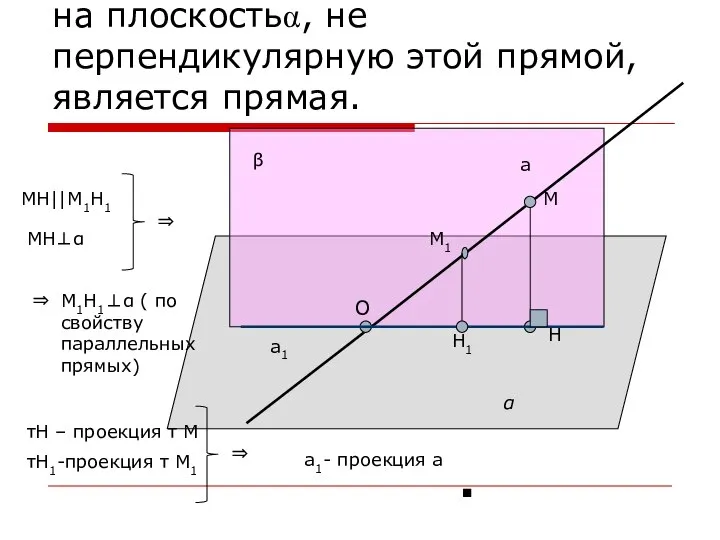
- 5. Докажем, что проекцией прямой а на плоскостьα, не перпендикулярную этой прямой, является прямая. а α О
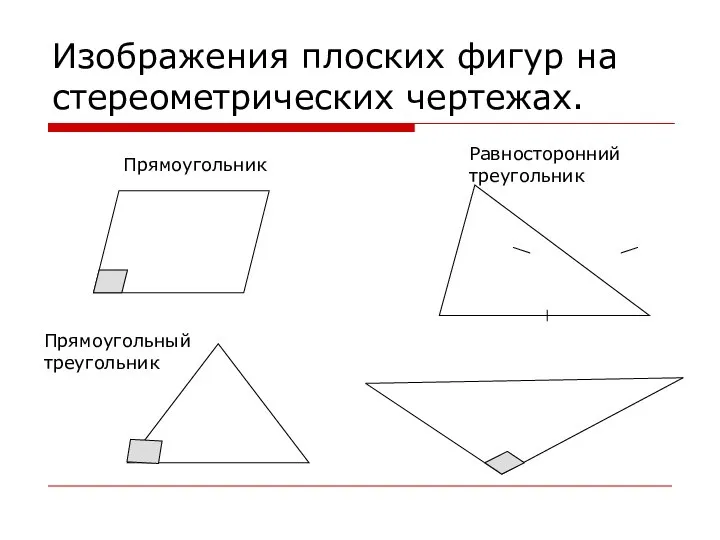
- 6. Изображения плоских фигур на стереометрических чертежах. Прямоугольник Прямоугольный треугольник Равносторонний треугольник
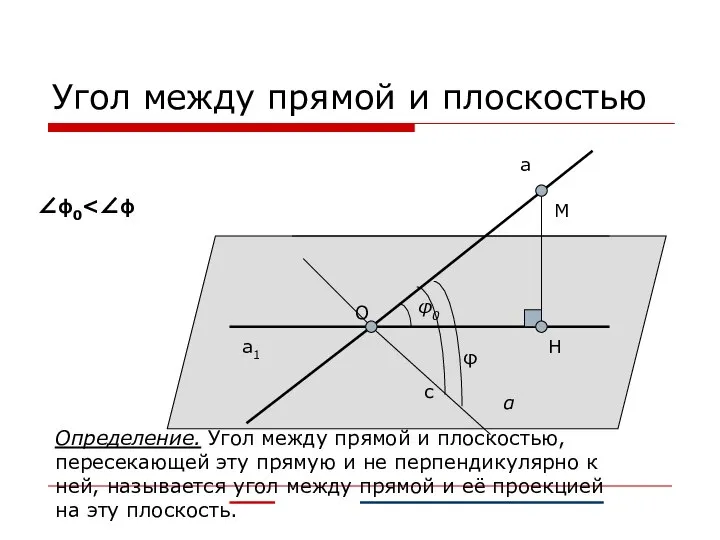
- 7. Угол между прямой и плоскостью а а1 α φ0 с φ H M O Определение. Угол
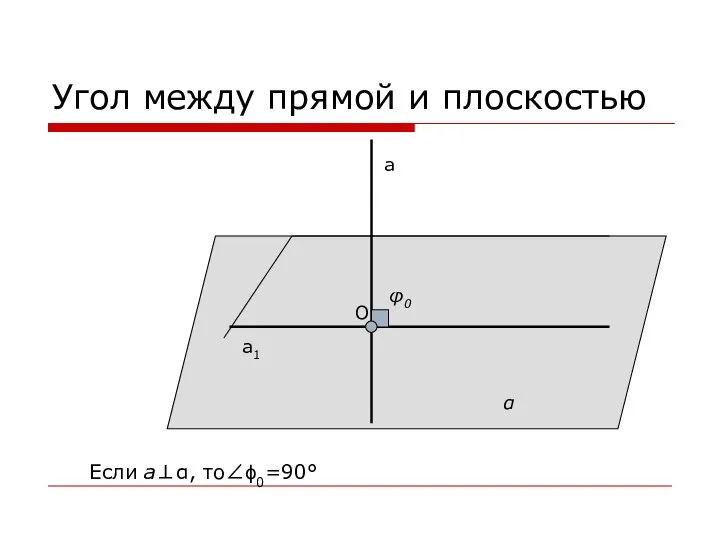
- 8. Угол между прямой и плоскостью а а1 α φ0 O Если а⊥α, то∠ϕ0=90°
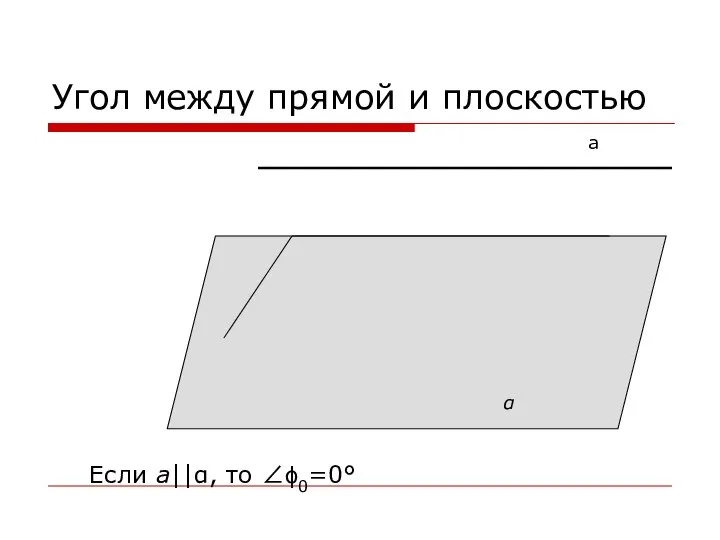
- 9. Угол между прямой и плоскостью а α Если а⎪⎪α, то ∠ϕ0=0°
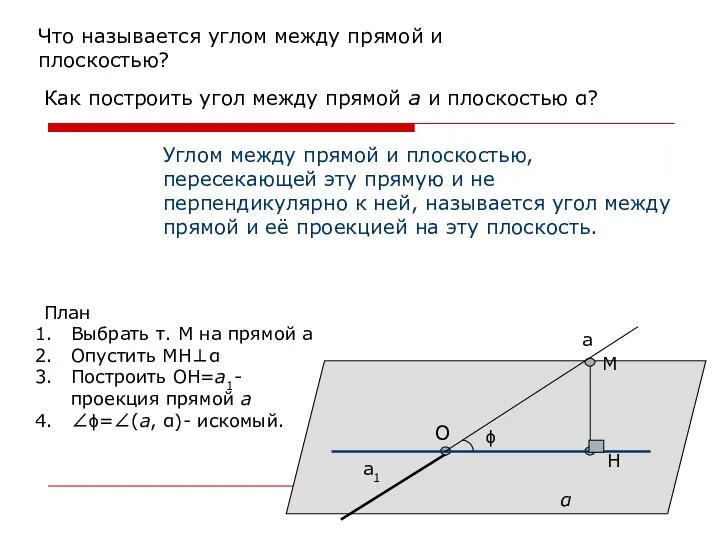
- 10. Что называется углом между прямой и плоскостью? Углом между прямой и плоскостью, пересекающей эту прямую и
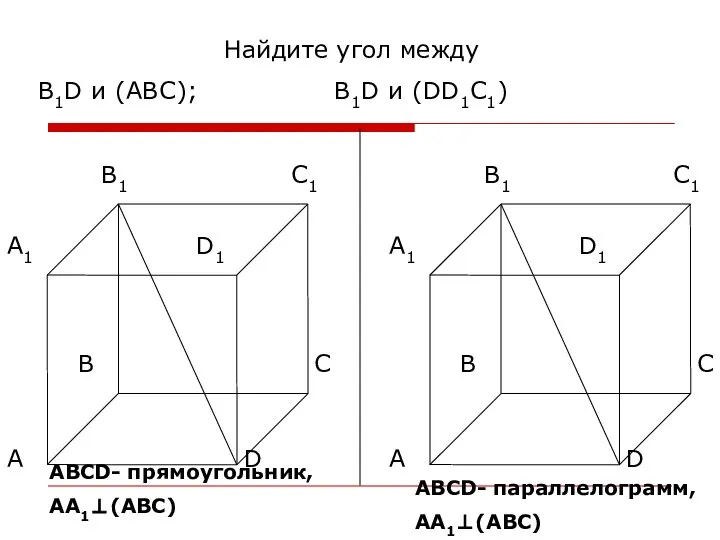
- 11. Найдите угол между В1D и (ABC); В1D и (DD1C1) АВСD- прямоугольник, АА1⊥(АВС) АВСD- параллелограмм, АА1⊥(АВС)
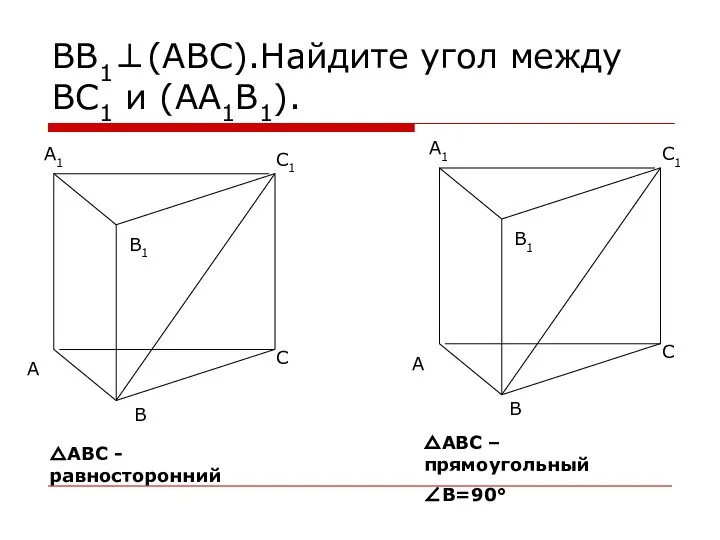
- 12. ВВ1⊥(АВС).Найдите угол между ВС1 и (АА1В1). △АВС - равносторонний △АВС – прямоугольный ∠В=90°
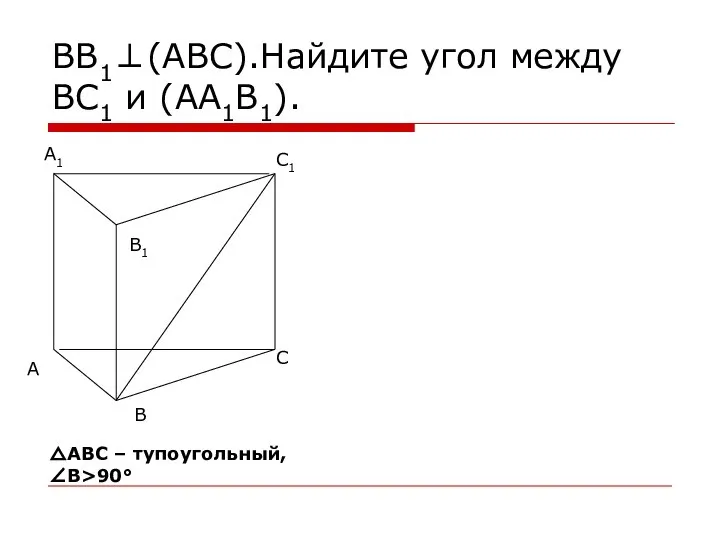
- 13. ВВ1⊥(АВС).Найдите угол между ВС1 и (АА1В1). △АВС – тупоугольный, ∠В>90°
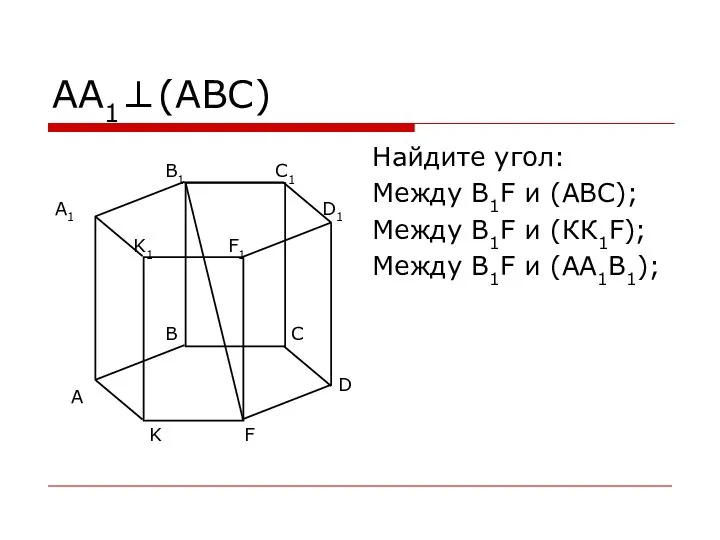
- 14. АА1⊥(АВС) Найдите угол: Между В1F и (АВС); Между В1F и (КК1F); Между В1F и (АА1В1);
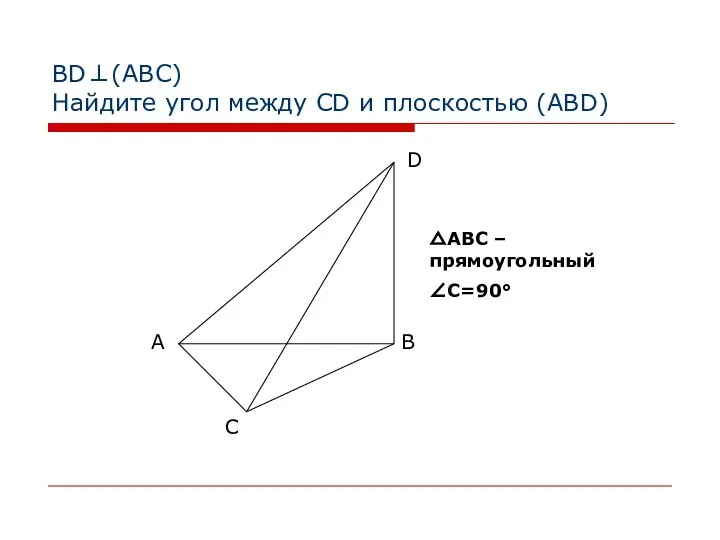
- 15. BD⊥(АВС) Найдите угол между CD и плоскостью (ABD) △АВС – прямоугольный ∠C=90°
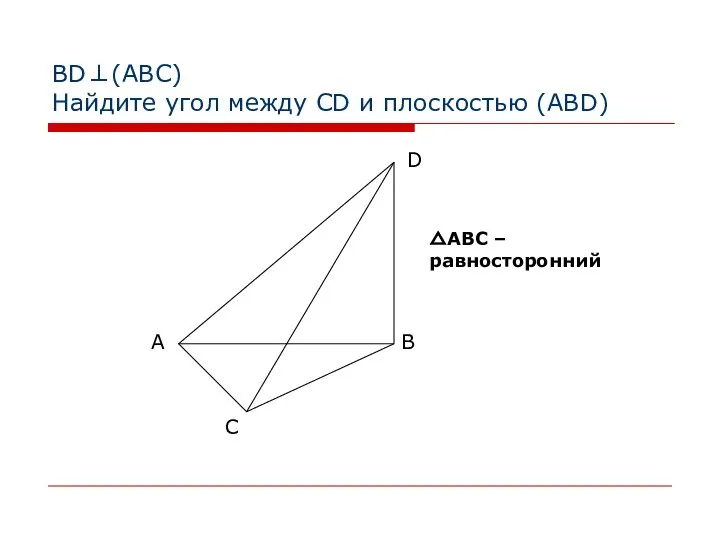
- 16. BD⊥(АВС) Найдите угол между CD и плоскостью (ABD) △АВС – равносторонний
- 18. Скачать презентацию

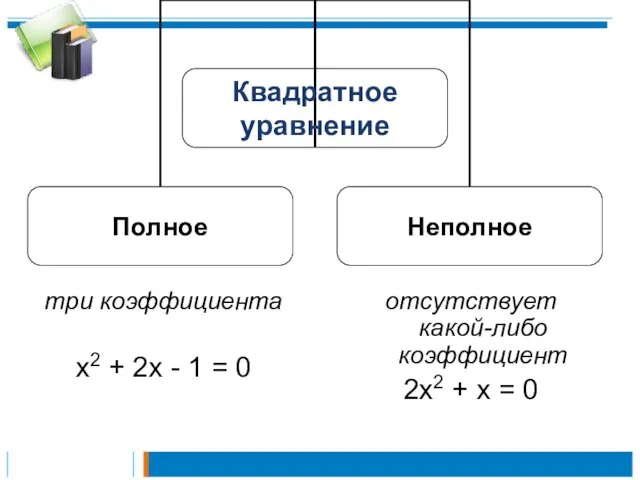 Неполные квадратные уравнения
Неполные квадратные уравнения Умножение одночленов. Возведение одночлена в степень
Умножение одночленов. Возведение одночлена в степень Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Геометрия. Повторение
Геометрия. Повторение Векторная алгебра. Основные определения
Векторная алгебра. Основные определения Вычисление площадей плоских фигур. Трапеция
Вычисление площадей плоских фигур. Трапеция Математический диктант
Математический диктант Контрольная работа
Контрольная работа Граф. Построение графов
Граф. Построение графов Мир логарифмов. 11 класс
Мир логарифмов. 11 класс Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Домашняя работа по математике
Домашняя работа по математике Цветочное настроение. Математика
Цветочное настроение. Математика Решение систем линейных неравенств с одной переменной (9 класс)
Решение систем линейных неравенств с одной переменной (9 класс) Надежность технических систем
Надежность технических систем Работа с числами
Работа с числами Функции одной и нескольких переменных
Функции одной и нескольких переменных Презентация на тему Преобразование графиков функций на координатной плоскости
Презентация на тему Преобразование графиков функций на координатной плоскости  Знакомство с линейкой
Знакомство с линейкой Ось симметрии фигуры
Ось симметрии фигуры Числовые великаны вокруг и внутри нас
Числовые великаны вокруг и внутри нас Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости Статистика. Введение в теорию вероятности. Основные понятия
Статистика. Введение в теорию вероятности. Основные понятия Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Сфера и шар
Сфера и шар История появления тригонометрии
История появления тригонометрии Функция y = x2 и её график
Функция y = x2 и её график Действия с числами, записанными в стандартном виде
Действия с числами, записанными в стандартном виде