Слайд 2
Выражения и их тождественные преобразования

Слайд 3
Математический язык –искусственный язык

Слайд 4Математический алфавит
Цифры: 0,1,2,3,4,5,6,7,8,9
Знаки операций: +, -, •, :
Знаки отношений: =, <, >
Строчные

буквы латинского алфавита: a, b, c и т.д.
Технические знаки: ( ), {}
Слайд 5Числовое выражение – это записи, образованные из чисел, знаков действий и скобок

- пример: 3+6, 3-4 •(2+5), 28:7
Значение числового выражения - результат выполнения арифметических действий, указанных в выражении (или само число)
- пример: выражение 3 • 2 - 4 , его значение 2
Слайд 6Числовые выражения, не имеющие смысла
8 : (4 - 4 ) –

делить на нуль нельзя!
7 – 9 (на множестве натуральных чисел)
Слайд 7Какие выражения не имеют смысла?
1)
2)
3) 10 + 20 – 45 (на множестве

N)
4)
5) 10 + (20 – 45) (на множестве Z)
6)
7)
Слайд 8Выражения с переменной
2а+3
- Если а = 7, то 2 • 7 +

3
Если а = 0, то 2 • 0 + 3
- Если а = - 4, то 2 • (-4) + 3
Буква а – переменная, а сама запись
2а+ 3 – выражение с переменной
Слайд 9Символы, с помощью которых обозначают переменную:
Буквы: а, b, c
Квадратик: □ (например,

2 • □ + 3)
Слайд 10Область определения выражения – множество значений, получаемых при подстановке чисел вместо переменной,

при которых данное выражение имеет смысл.
Например:
5 : (x - 7)
Область определения: все действительные числа, кроме 7
Слайд 11Найдите область определения выражения:
1)
2)
3)

Слайд 13Точное определение числового выражения
Если f и g – числовые выражения, то (f)

+ (g), (f) - (g), (f) : (g) числовые выражения.
Считают, что каждое число также является числовым выражением
Слайд 14(7) + (5) (6) : (2)
37 – 12 + 62 – 17
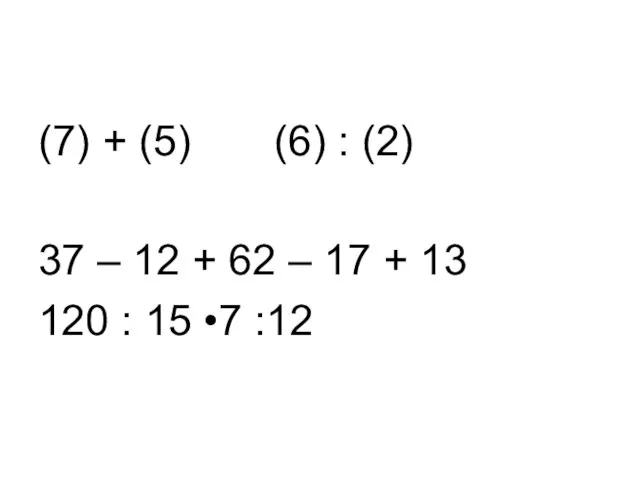
+ 13
120 : 15 •7 :12
Слайд 15Действия второй ступени – умножение и деление
Действия первой ступени – сложение и

вычитание
Порядок: слева - направо
Слайд 16(12 • 4 : 3) +(5 • 8 : 2 • 7)
12
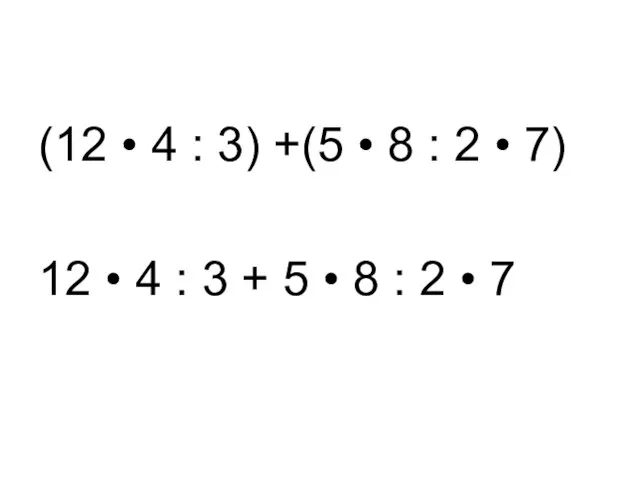
• 4 : 3 + 5 • 8 : 2 • 7
Слайд 17Найти значение выражения двумя способами:
3x(x-2) +4(x-2) при x = 6

Слайд 18Два выражения называются тождественно равными, если при любых значениях переменной из области

определения выражения их соответственные значения равны
Слайд 195(x-2) = 5x -10
Замена выражения другим, тождественно равным ему на некотором множестве,

называется тождественным преобразованием данного выражения на этом множестве.
Слайд 20Задача
Разложите на множители выражение:
Прокомментируйте, какие законы сложения и умножения вы использовали?

Слайд 2135 • 4 = (30 + 5) • 4 = 30 •

4 + 5 • 4 = 120 + 20 = 40
Использованные принципы:
- свойство дистрибутивности умножения относительно сложения;
принцип записи чисел в десятичной системе счисления;
правила умножения и сложения натуральных чисел;
Слайд 22Числовые равенства
f = g, где f и g – числовые выражения
Числовое равенство–

это высказывание, истинное или ложное.
Числовое равенство истинно, если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают.
Слайд 23Некоторые свойства числовых равенств
Если к обеим частям истинного числового равенства прибавить одно

и то же числовое выражение, имеющее смысл ,то получим также истинное числовое равенство.
Если обе части истинного числового равенства умножить на одно и тоже числовое выражение, имеющее смысл, то также получим истинное числовое равенство.
Слайд 24Числовые неравенства
f < g (или f > g ), где f и

g – числовые выражения
Числовое неравенство– это высказывание, истинное или ложное.
6 + 2 > 13 – 7 истина
6 + 2 < 13 – 7 ложь











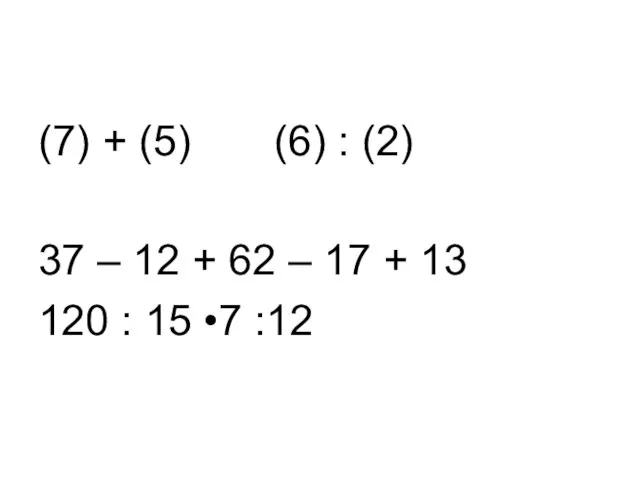

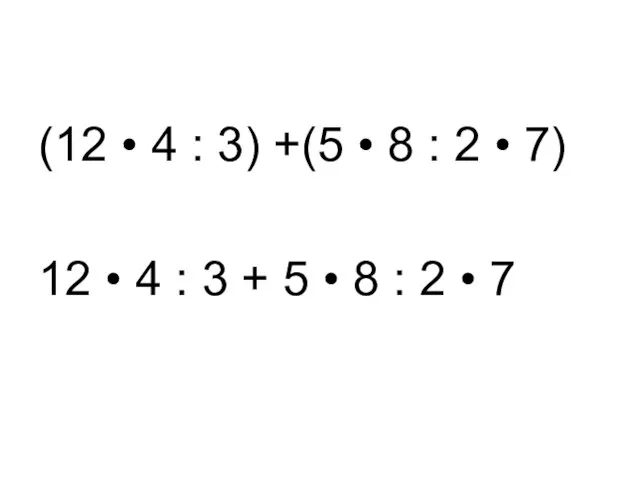








 СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи Перетворення подібності. Гомотерапія
Перетворення подібності. Гомотерапія Венегрет. Урок
Венегрет. Урок Аналитические функции
Аналитические функции Презентация на тему Площадь прямоугольника: практикум
Презентация на тему Площадь прямоугольника: практикум  Probability Distributions
Probability Distributions Стационарный режим теплообмена с фазовым переходом
Стационарный режим теплообмена с фазовым переходом Презентация на тему Решение задач по теме "Пирамида" 10 класс
Презентация на тему Решение задач по теме "Пирамида" 10 класс  Где встречаются многогранники и в каких областях могут применяться
Где встречаются многогранники и в каких областях могут применяться Влияние коэффициентов линейной функции на ее график
Влияние коэффициентов линейной функции на ее график Умножение на двузначные и трёхзначные числа
Умножение на двузначные и трёхзначные числа Презентация на тему Степени
Презентация на тему Степени  Найдите значение выражения
Найдите значение выражения Эки эселенген бурчтун тригонометриялык функциялары
Эки эселенген бурчтун тригонометриялык функциялары Многоугольники
Многоугольники Вычитание предшествующего числа
Вычитание предшествующего числа Функция у=1/х и её график
Функция у=1/х и её график Стереометрия
Стереометрия Презентация на тему Действия с целыми числами
Презентация на тему Действия с целыми числами  Комплексные числа
Комплексные числа The formal normal form degenerate singular points in the case of case of focus
The formal normal form degenerate singular points in the case of case of focus Презентация к уроку геометрии _Сравнение отрезков и углов_
Презентация к уроку геометрии _Сравнение отрезков и углов_ Углы в треугольниках
Углы в треугольниках Презентация по математике "Праздник чисел «5 плюс »" -
Презентация по математике "Праздник чисел «5 плюс »" -  Законы алгебры логики
Законы алгебры логики Использование циклов
Использование циклов Алгоритм как один из методов организации самоподготовки воспитанников
Алгоритм как один из методов организации самоподготовки воспитанников Вычитание натуральных чисел
Вычитание натуральных чисел