Векторы

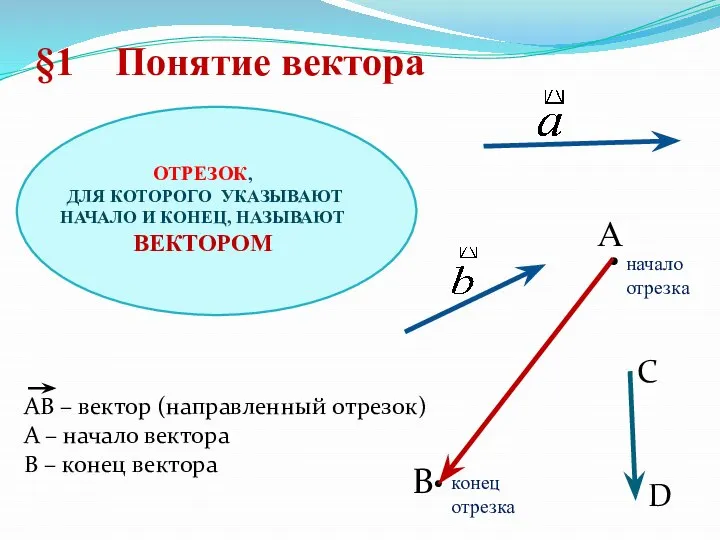
B
•
АВ – вектор (направленный отрезок)
А – начало вектора
В – конец вектора
§1 Понятие вектора
•
С
D
ОТРЕЗОК,
ДЛЯ КОТОРОГО УКАЗЫВАЮТ НАЧАЛО И КОНЕЦ, НАЗЫВАЮТ ВЕКТОРОМ
A
начало
отрезка
конец
отрезка

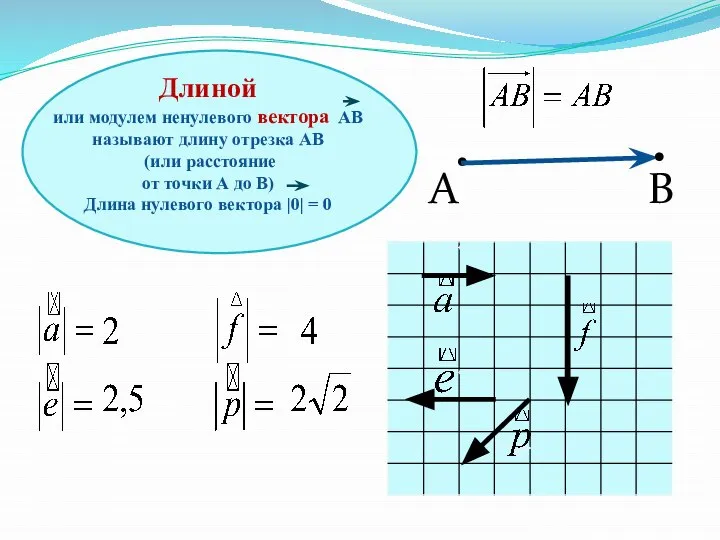
Длиной
или модулем ненулевого вектора АВ называют длину отрезка АВ
(или расстояние
от точки А до В)
Длина нулевого вектора |0| = 0
•
A
B
•

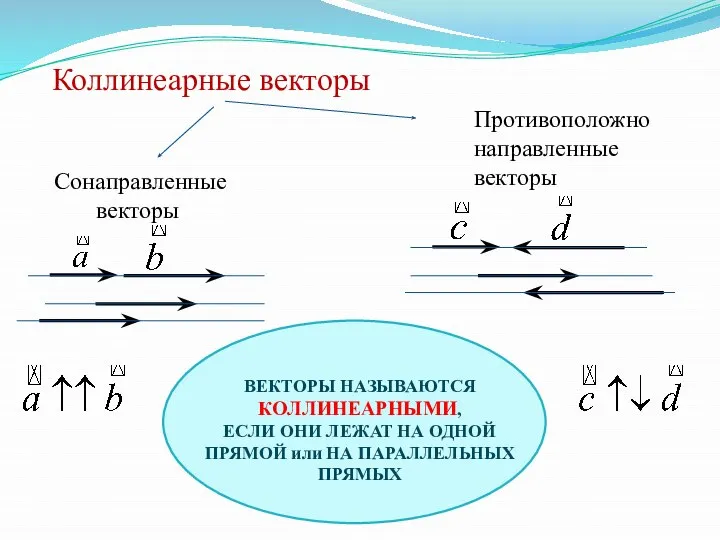
Сонаправленные векторы
Противоположно направленные векторы
Коллинеарные векторы
ВЕКТОРЫ НАЗЫВАЮТСЯ КОЛЛИНЕАРНЫМИ,
ЕСЛИ ОНИ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ или НА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

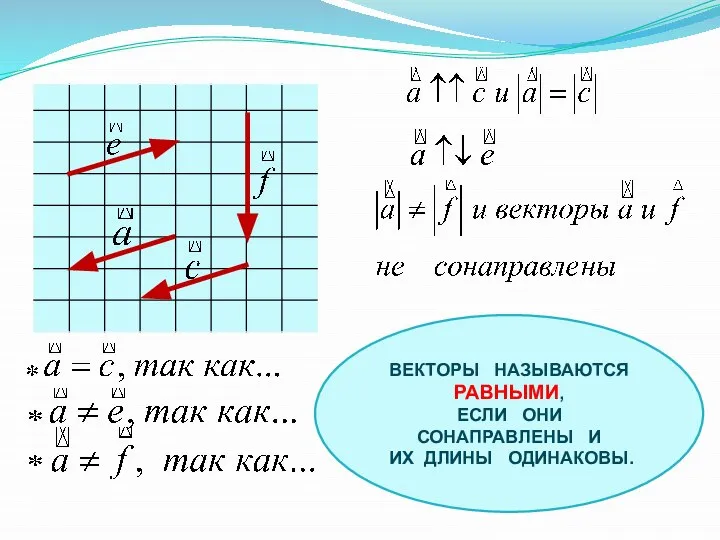
ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ,
ЕСЛИ ОНИ СОНАПРАВЛЕНЫ И
ИХ ДЛИНЫ ОДИНАКОВЫ.

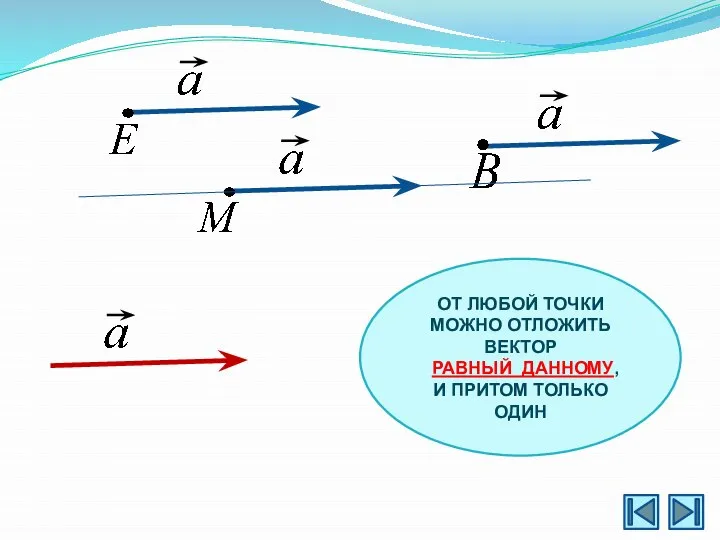
ОТ ЛЮБОЙ ТОЧКИ МОЖНО ОТЛОЖИТЬ ВЕКТОР
РАВНЫЙ ДАННОМУ, И ПРИТОМ ТОЛЬКО ОДИН

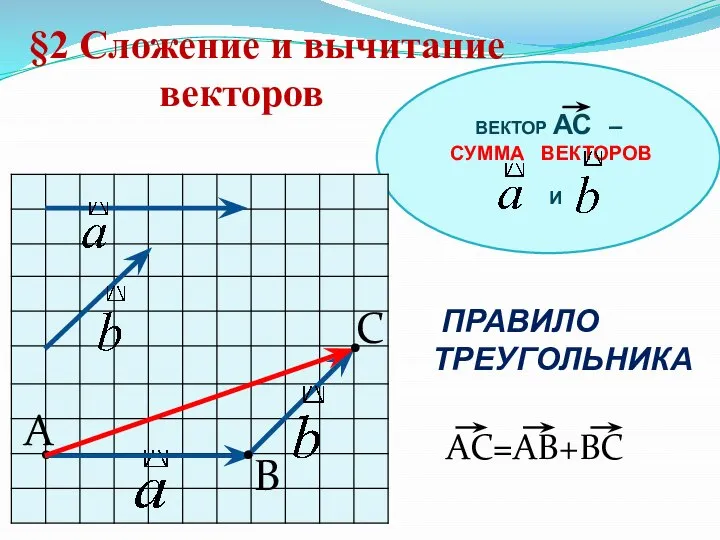
ВЕКТОР АС –
СУММА ВЕКТОРОВ
И
§2 Сложение и вычитание
векторов
ПРАВИЛО
ТРЕУГОЛЬНИКА
•
A
B
•
•
AС=АВ+ВС
С

•
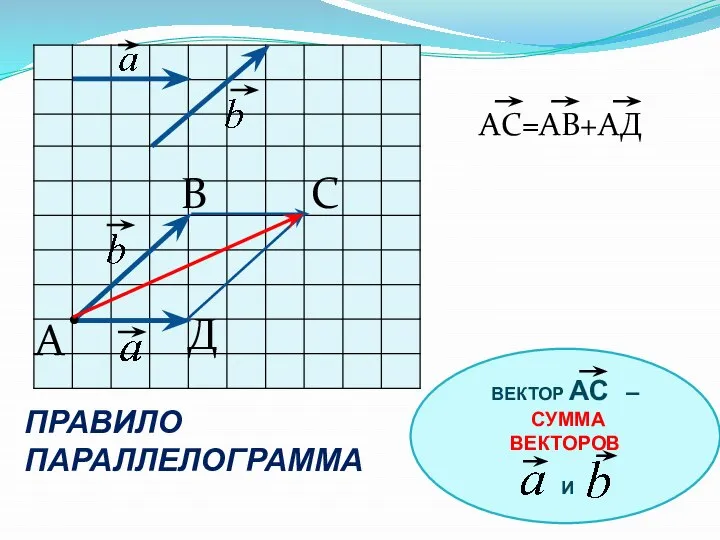
A
С
B
Д
ПРАВИЛО
ПАРАЛЛЕЛОГРАММА
AС=АВ+АД
ВЕКТОР АС –
СУММА ВЕКТОРОВ
И

ЗАКОНЫ
СЛОЖЕНИЯ ВЕКТОРОВ

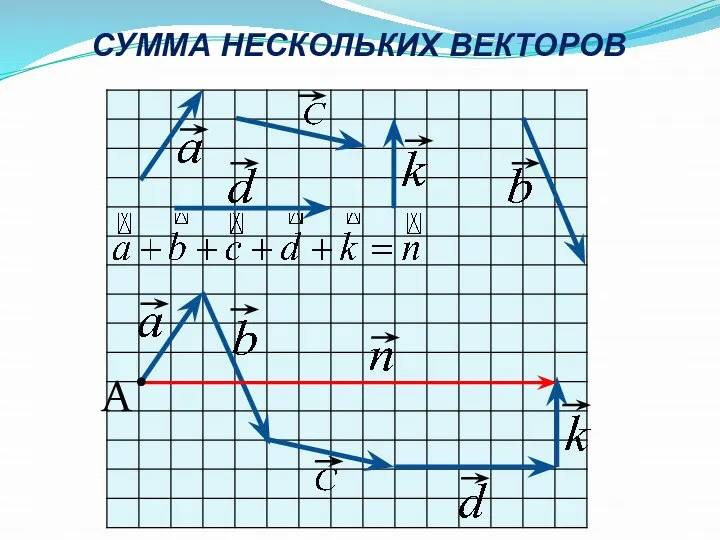
СУММА НЕСКОЛЬКИХ ВЕКТОРОВ
•
A

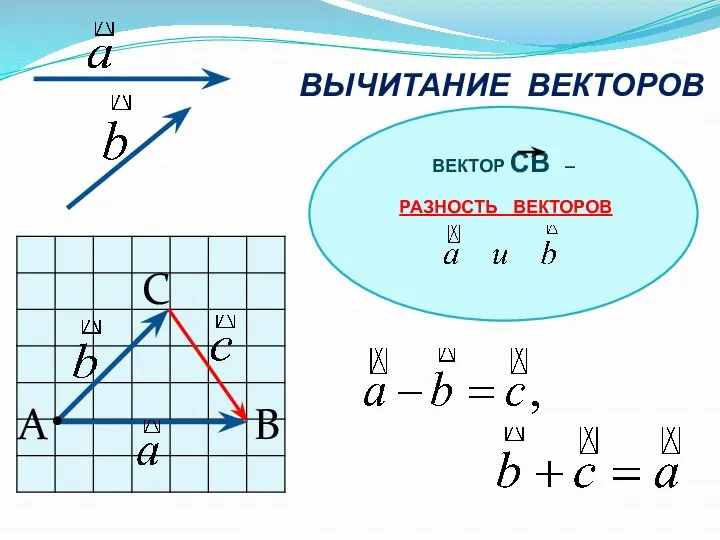
ВЫЧИТАНИЕ ВЕКТОРОВ
А
B
С
•
ВЕКТОР СВ –
РАЗНОСТЬ ВЕКТОРОВ

ВЕКТОРЫ И
ПРОТИВОПОЛОЖНЫЕ ВЕКТОРЫ

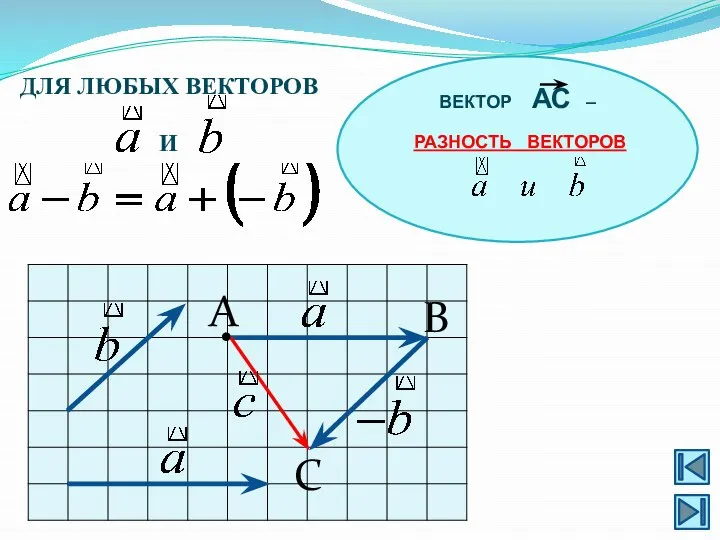
А
B
С
•
ВЕКТОР АС –
РАЗНОСТЬ ВЕКТОРОВ
ДЛЯ ЛЮБЫХ ВЕКТОРОВ
И

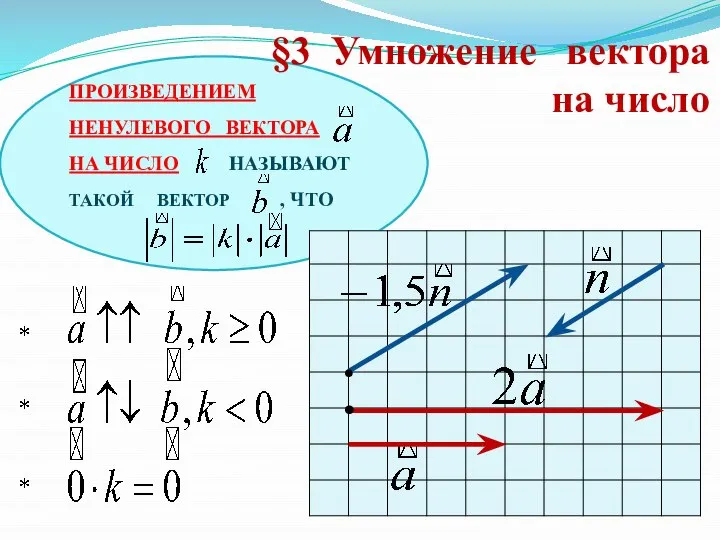
ПРОИЗВЕДЕНИЕМ НЕНУЛЕВОГО ВЕКТОРА НА ЧИСЛО НАЗЫВАЮТ ТАКОЙ ВЕКТОР , ЧТО
§3 Умножение вектора
на число
•
•

Основные свойства
умножения вектора
на число
Следствия

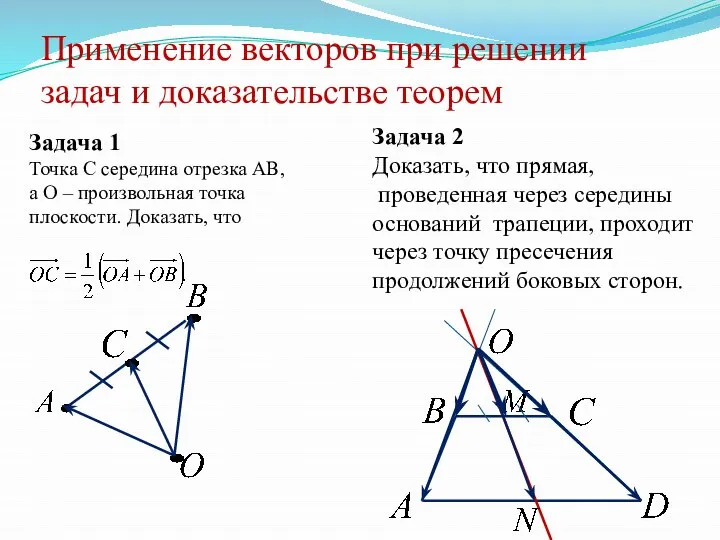
Применение векторов при решении
задач и доказательстве теорем
Задача 1
Точка С середина отрезка АВ,
а О – произвольная точка
плоскости. Доказать, что
Задача 2
Доказать, что прямая,
проведенная через середины
оснований трапеции, проходит
через точку пресечения
продолжений боковых сторон.

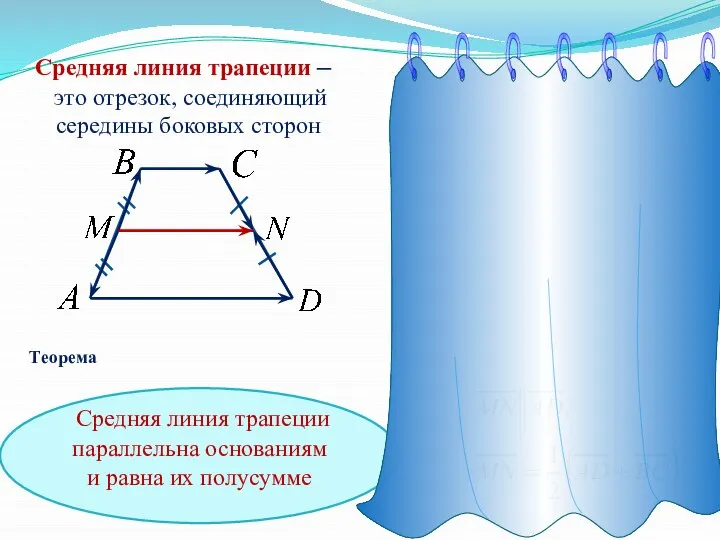
Средняя линия трапеции –
это отрезок, соединяющий
середины боковых сторон
Средняя линия трапеции параллельна основаниям и равна их полусумме
Теорема

Самостоятельная работа
Вариант 1.
1. Перечертить рисунок в тетрадь. Построить векторы и , такие что
.
2. Выписать сонаправленные, противоположно направленные и равные векторы
D С
А В
3. ABCD – параллелограмм. Доказать, что