Содержание
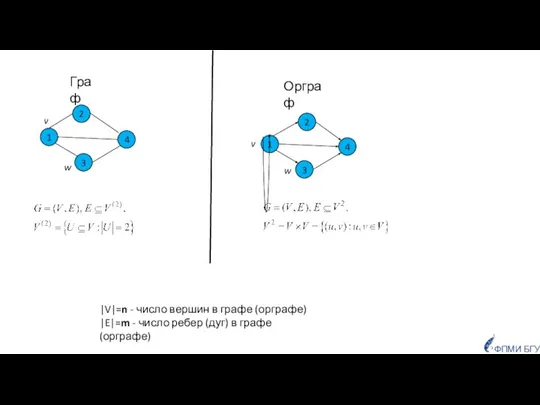
- 2. ФПМИ БГУ |V|=n - число вершин в графе (орграфе) |E|=m - число ребер (дуг) в графе
- 3. Структуры данных для представления графа (орграфа) ФПМИ БГУ Матрица смежности Списки смежности Матрица инцидентности Списки дуг
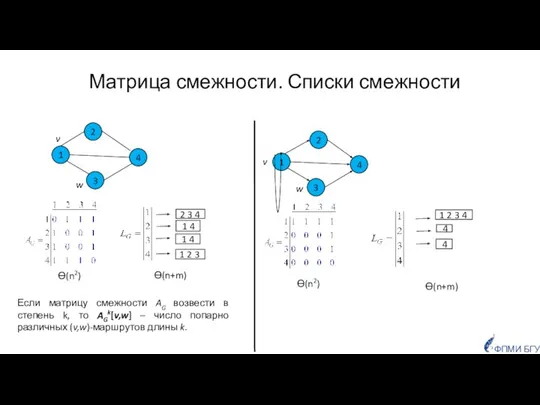
- 4. Матрица смежности. Списки смежности 2 3 4 1 4 1 4 1 2 3 1 2
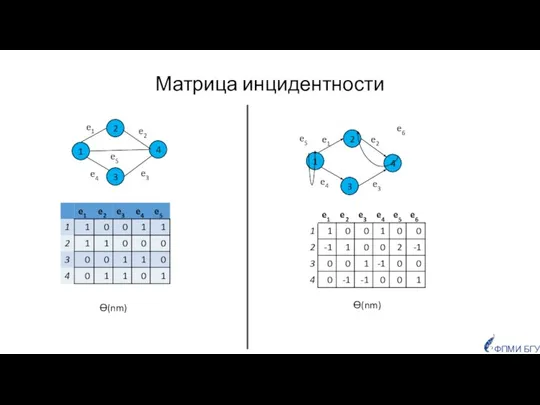
- 5. Матрица инцидентности Ө(nm) Ө(nm) ФПМИ БГУ
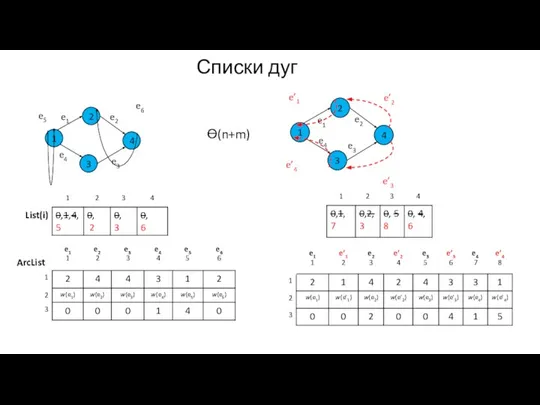
- 6. Списки дуг 1 3 4 2 e4 e1 e2 e3 e’2 Ө(n+m) e’3 e’4 e’1
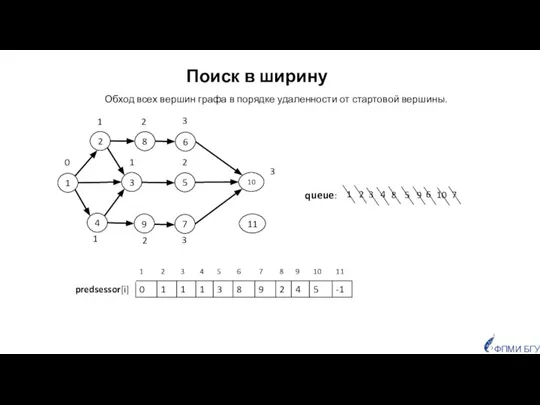
- 7. Поиск в ширину (англ. BFS - Breadth First Search) ФПМИ БГУ
- 8. 1 1 1 0 2 2 2 3 Поиск в ширину 1 6 5 4 3
- 9. Задание графа матрицей смежности Время работы О(n2) Время работы О(n+m) v u1 uk ФПМИ БГУ Задание
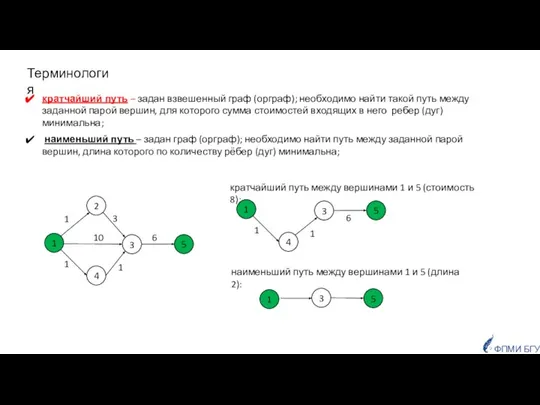
- 10. кратчайший путь – задан взвешенный граф (орграф); необходимо найти такой путь между заданной парой вершин, для
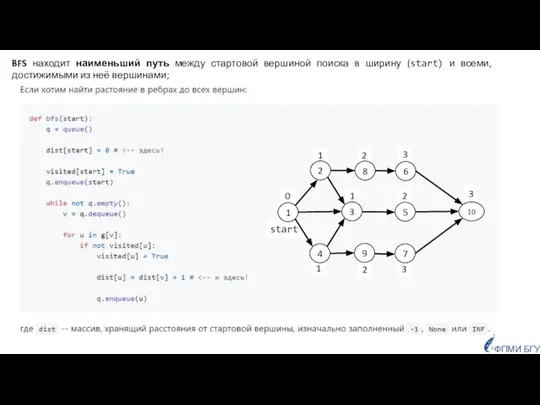
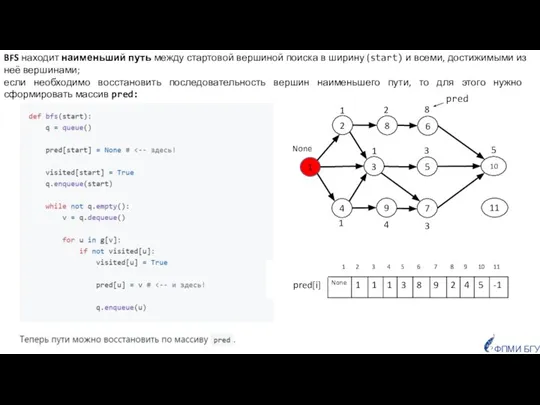
- 11. ФПМИ БГУ BFS находит наименьший путь между стартовой вершиной поиска в ширину (start) и всеми, достижимыми
- 12. 1 1 3 5 4 3 1 6 5 4 3 2 7 10 8 9
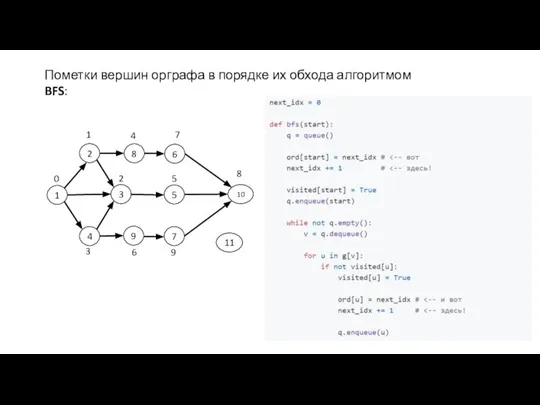
- 13. 1 4 7 3 6 9 2 0 5 8 Пометки вершин орграфа в порядке их
- 14. Свойством двудольного графа является то, что если две вершины графа смежны, то они принадлежат разным долям.
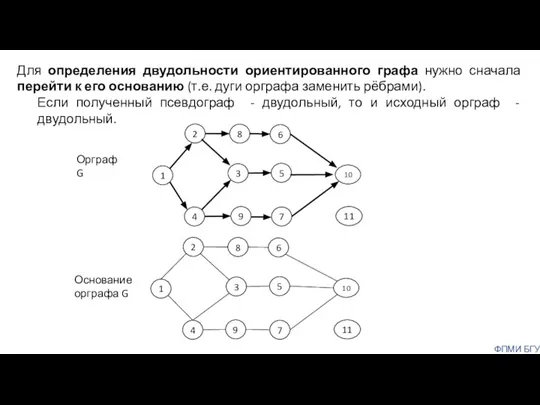
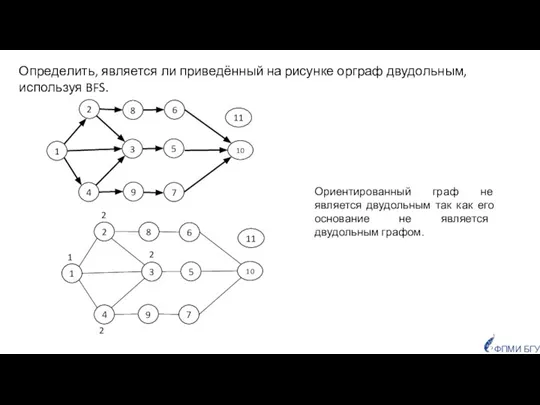
- 15. Орграф G Основание орграфа G ФПМИ БГУ Для определения двудольности ориентированного графа нужно сначала перейти к
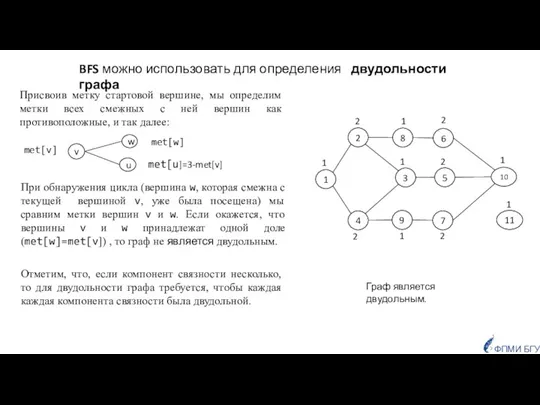
- 16. 1 6 5 4 3 2 7 10 8 9 11 При обнаружения цикла (вершина w,
- 17. 1 2 2 2 1 6 5 4 3 2 7 10 8 9 11 1
- 18. 1 6 5 4 3 2 7 10 8 9 11 Всякий максимальный по включению связный
- 19. ФПМИ БГУ BFS можно использовать для решения следующих задач Поиска маршрута между заданной парой вершин. Поиска
- 20. Эйлеров цикл в графе Для связного графа эйлеров цикл – это цикл, который содержит все рёбра
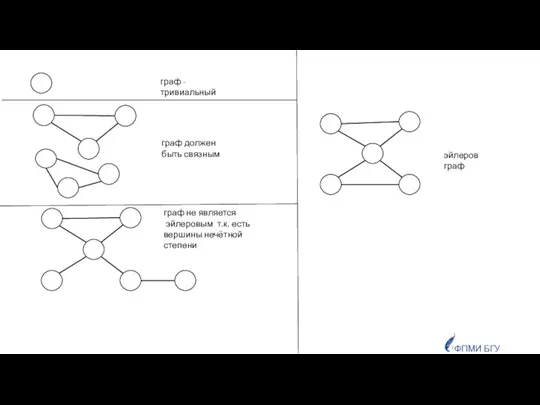
- 21. ФПМИ БГУ эйлеров граф граф не является эйлеровым т.к. есть вершины нечётной степени граф должен быть
- 22. ФПМИ БГУ Граф эйлеров, если мы можем его нарисовать, не отрывая руку от бумаги: стартуем из
- 23. Алгоритм построения эйлерова цикла в графе Абстрактные типы данных очередь (queue) и стек (stack) – пустые.
- 24. 1 5 3 4 2 Алгоритм построения эйлерова цикла графа Структуры данных очередь (queue) и стек
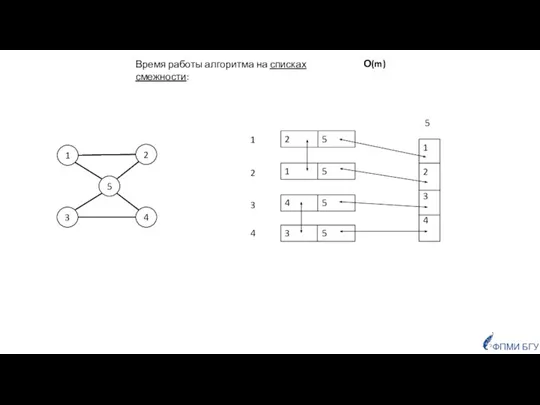
- 25. 1 5 3 4 2 Время работы алгоритма на списках смежности: О(m) ФПМИ БГУ 1 2
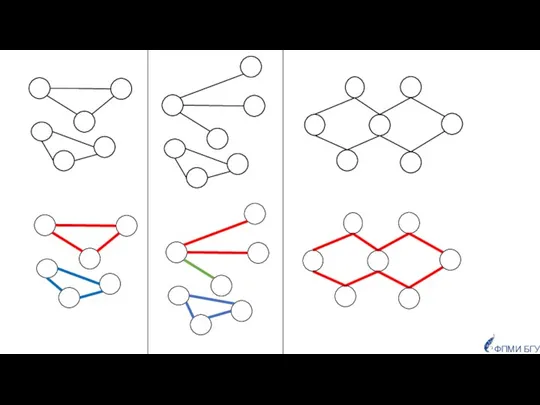
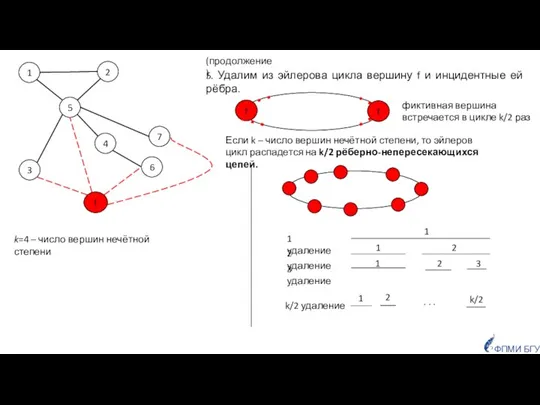
- 26. Задан граф (не обязательно связный). Необходимо покрыть граф наименьшим числом рёберно-непересекающихся цепей. Цепи могут быть открытыми
- 27. ФПМИ БГУ
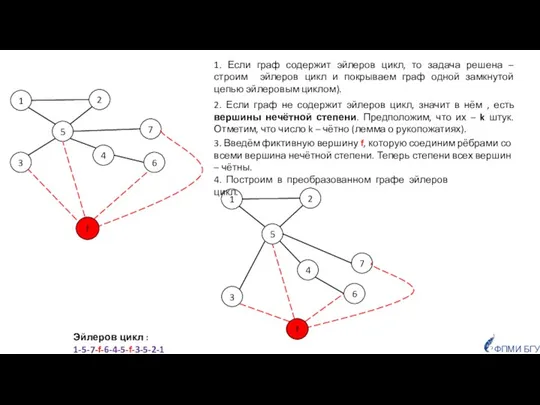
- 28. 1 5 3 4 2 6 7 ФПМИ БГУ 1. Если граф содержит эйлеров цикл, то
- 29. 5. Удалим из эйлерова цикла вершину f и инцидентные ей рёбра. ФПМИ БГУ 1 5 3
- 30. ФПМИ БГУ
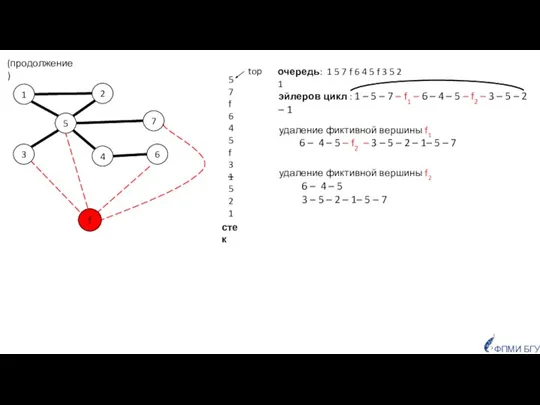
- 31. 1 5 3 4 2 6 ФПМИ БГУ стек эйлеров цикл : 1 – 5 –
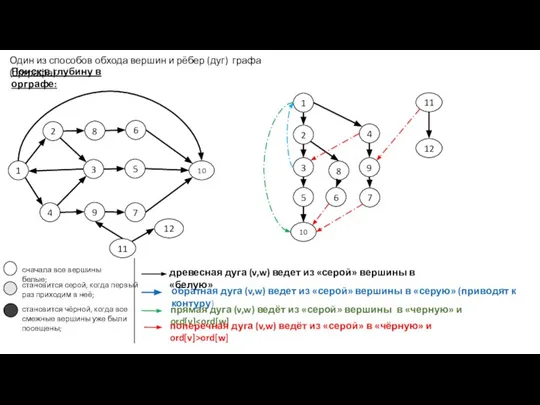
- 32. Поиск в глубину ( англ. DFS - Depth First Search)
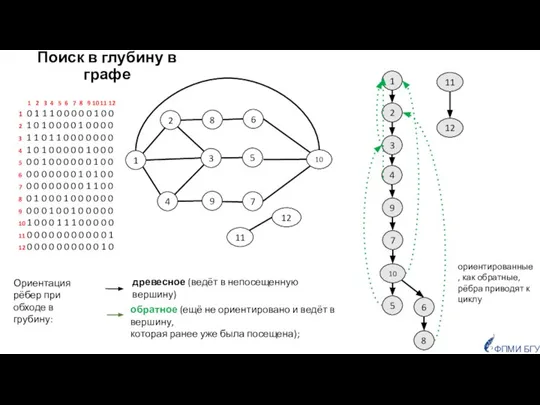
- 33. 1 6 5 4 3 2 7 10 8 9 11 1 2 3 5 10
- 34. 1 6 5 4 3 2 7 10 8 9 11 1 2 3 5 10
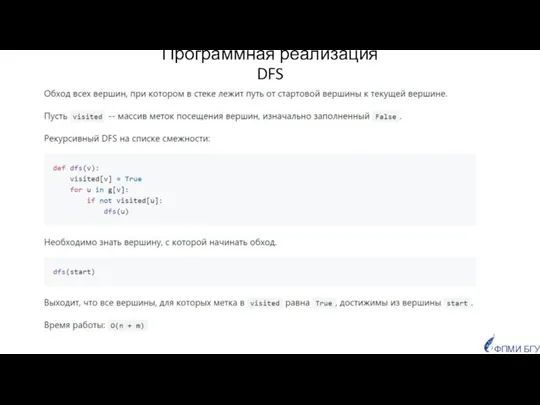
- 35. ФПМИ БГУ Программная реализация DFS
- 36. ФПМИ БГУ
- 37. Нерекурсивный DFS на списке смежности Здесь last - массив, в котором для каждой вершины v хранится
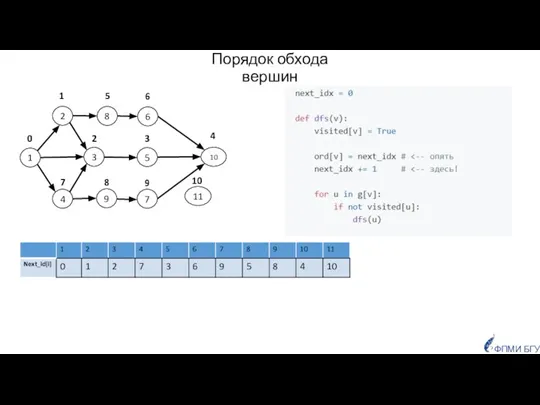
- 38. 1 6 5 4 3 2 7 10 8 9 11 1 2 7 0 5
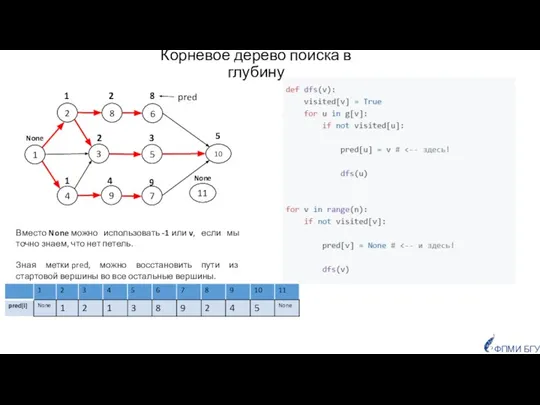
- 39. Вместо None можно использовать -1 или v, если мы точно знаем, что нет петель. Зная метки
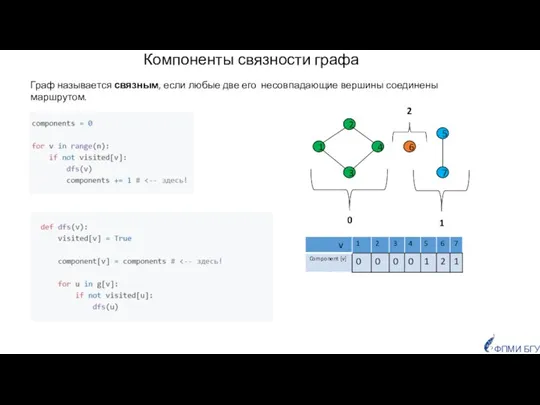
- 40. Компоненты связности графа 0 2 1 Граф называется связным, если любые две его несовпадающие вершины соединены
- 41. Определение двудольности графа 1 2 3 4 True False True is_bipartite=False ФПМИ БГУ
- 42. Топологическая сортировка ФПМИ БГУ
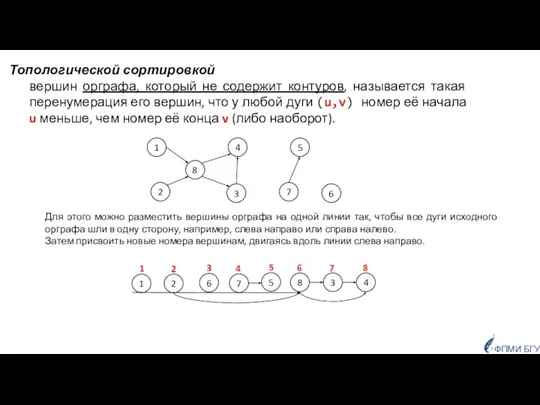
- 43. Топологической сортировкой вершин орграфа, который не содержит контуров, называется такая перенумерация его вершин, что у любой
- 44. Для выполнения топологической сортировки вершин ациклического орграфа можно использовать, алгоритмы А. Кана (1962) Р. Тарьяна (1976)
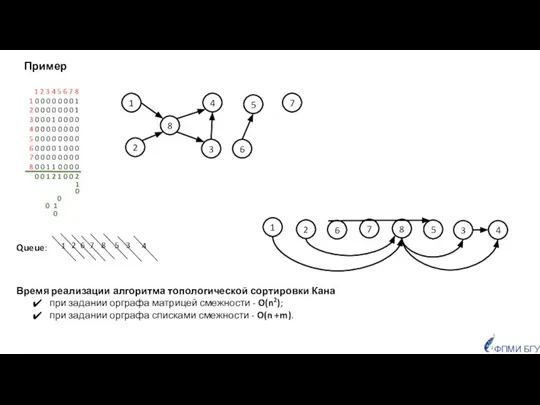
- 45. Алгоритм Кана Пока в графе G существуют вершины без входящих дуг, выполнять следующие действия: найти любую
- 46. 1 2 3 4 5 1 2 1 2 ФПМИ БГУ Проверить, всем ли вершинам были
- 47. 1 5 2 3 7 6 4 8 1 2 6 5 7 8 3 4
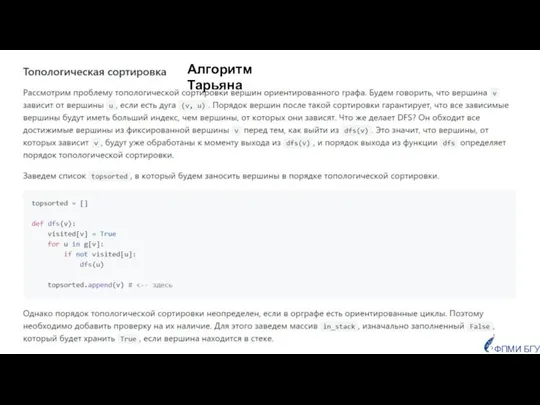
- 48. Алгоритм Тарьяна ФПМИ БГУ
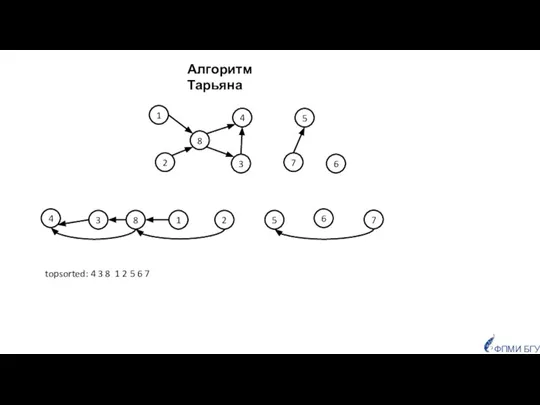
- 49. 1 5 2 3 6 7 4 8 topsorted: 4 3 8 1 2 5 6
- 50. ФПМИ БГУ
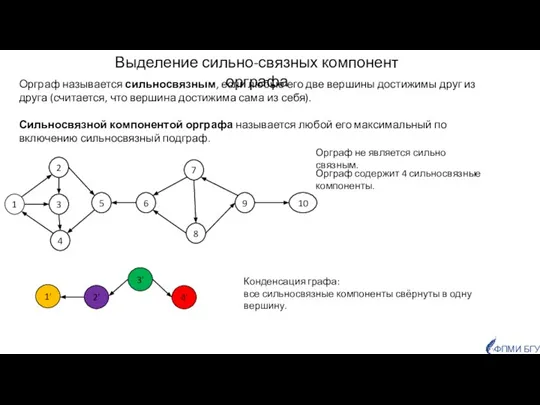
- 51. Выделение сильно-связных компонент орграфа Орграф называется сильносвязным, если любые его две вершины достижимы друг из друга
- 52. Алгоритм Косарайю - Шарира выделения сильно-связных компонент орграфа (основанный на DFS) 1978 год Самбрасива Рао Косарайю/Косараджу
- 53. Алгоритм Косарайю - Шарира 1 3 2 4 5 8 7 6 9 10 1 3
- 54. Обоснование корректности алгоритма Косарайю-Шарира Рассмотрим конденсацию графа G, то есть граф, в котором все сильно связные
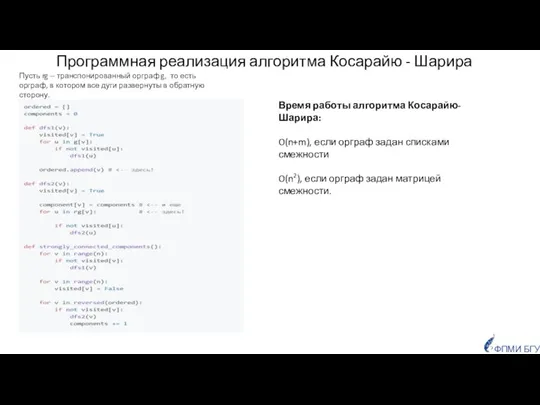
- 55. Пусть rg -- транспонированный орграф g, то есть орграф, в котором все дуги развернуты в обратную
- 56. ФПМИ БГУ DFS можно использовать для решения следующих задач Поиск маршрута между заданной парой вершин. Определение
- 57. Общие задачи в iRunner для закрепления навыков 0.4 Матрица смежности 0.5. Канонический вид (по списку дуг)
- 59. Скачать презентацию


























 Презентация на тему Связь между слагаемыми и суммой
Презентация на тему Связь между слагаемыми и суммой  Экстремумы (1)
Экстремумы (1) Урок 23
Урок 23 Перпендикулярные прямые
Перпендикулярные прямые Своя игра. Треугольники
Своя игра. Треугольники Множество значений тригонометрических функций
Множество значений тригонометрических функций Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Презентация на тему Уравнение х2=а (8 класс)
Презентация на тему Уравнение х2=а (8 класс)  Арккосинус а. Решение уравнений
Арккосинус а. Решение уравнений Смежные и вертикальные углы
Смежные и вертикальные углы Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Параллельные прямые, перпендикулярные к плоскости
Параллельные прямые, перпендикулярные к плоскости Линейная функция
Линейная функция Многоугольники
Многоугольники Виды треугольников
Виды треугольников Введение в стереометрию
Введение в стереометрию Решение иррациональных уравнений
Решение иррациональных уравнений Анализ ошибок. Параллелепипеды. 10 класс
Анализ ошибок. Параллелепипеды. 10 класс Решение задач ЕГЭ по тригонометрии
Решение задач ЕГЭ по тригонометрии Числа 1 – 5 закрепление
Числа 1 – 5 закрепление Параметры четырехугольника
Параметры четырехугольника Случаи вычитания
Случаи вычитания Пивкин ИКС-34 (2)
Пивкин ИКС-34 (2) Приёмы устных вычислений вида 240 умножить на 4, 203 умножить на 4
Приёмы устных вычислений вида 240 умножить на 4, 203 умножить на 4 Powtórzenie do klasówki
Powtórzenie do klasówki Сложение натуральных чисел 5 класс МОУ «Усть-Мосихинская СОШ» Новосёлова Е.А.
Сложение натуральных чисел 5 класс МОУ «Усть-Мосихинская СОШ» Новосёлова Е.А. Теорема Безу. Схема Горнера
Теорема Безу. Схема Горнера