Применение социологических опросов для исследования ОМ (часть 2)

Применение социологических опросов для исследования ОМ
Часть 2

Учебные вопросы и литература
Литература:
Гаджиев, К. С. Политическая социология : учебное пособие для академического бакалавриата / К. С. Гаджиев. — Москва : Издательство Юрайт, 2019. — 208 с. — (Бакалавр. Академический курс). — ЭБС Юрайт. — URL: https://www.biblio-online.ru/bcode/433747 (дата обращения: 19.12.2019). - Текст : электронный.
Елисеев, С. М. Политическая социология : учебник и практикум для академического бакалавриата / С. М. Елисеев. — Москва : Издательство Юрайт, 2019. — 412 с. — (Бакалавр. Академический курс). — ЭБС Юрайт. — URL: https://www.biblio-online.ru/bcode/433207 (дата обращения: 19.12.2019). — Текст : электронный.
Лавриненко, В.Н. Исследование социально-экономических и политических процессов : учебник для бакалавров / В. Н. Лавриненко, Л. М. Путилова. — 3-е изд., перераб. и доп. — М. : Издательство Юрайт, 2019. — 251 с. — (Бакалавр и магистр. Академический курс) - URL: https://www.biblioonline.ru/bcode/426173 (дата обращения: 19.12.2019). - Текст : электронный.

Темы выступлений:
Информирование:
По социальным проблемам современной России
По политическим проблемам современной России
По международным проблемам
Доклады: Анкетирование и интервьюирование, их виды и особенности применения.
Область применения глубинных и экспертных интервью в рекламе и PR
Область применения фокус-группы в рекламе и PR (на конкретном примере).

Выборочный метод в социологических исследованиях
Учебные вопросы:
1. Расчет объема выборочной совокупности.
2. Логическая схема обработки и анализа информации самостоятельного социологического исследования

Следует ответить на два вопроса:
Насколько уверенными Вы должны быть в том, что полученные ответы отображают мнения генеральной совокупности?
Это предел погрешности. Итак, допустим, 90% членов выборки любят жевательную резинку со вкусом винограда. Предел погрешности в 5% добавляет по 5% с каждой стороны этого числа, что означает, что фактически 85-95% участников выборки любят жевательную резинку со вкусом винограда. 5% — наиболее часто используемый предел погрешности, но Вы можете устанавливать его значение от 1% до 10% в зависимости от опроса. Не рекомендуется поднимать этот показатель выше 10%.
Какова требуемая точность?

Насколько уверенными Вы должны быть в том, что выборка в точности представляет генеральную совокупность?
Это уровень доверия.
Уровень доверия — это вероятность того, что выборка является значимой для полученных результатов.
Расчет, как правило, производится следующим образом.
Если бы Вы в случайном порядке определили еще 30 выборок из данной совокупности, то как часто полученный Вами результат для одной выборки существенно отличался бы от результатов для других 30 выборок?
Уровень доверия в 95% означает, что в 95% случаев результаты совпадали бы.
95% — наиболее часто используемое значение, но Вы можете установить его на уровне 90% или 99% в зависимости от опроса.
Опускать значение уровня доверия ниже 90% не рекомендуется.

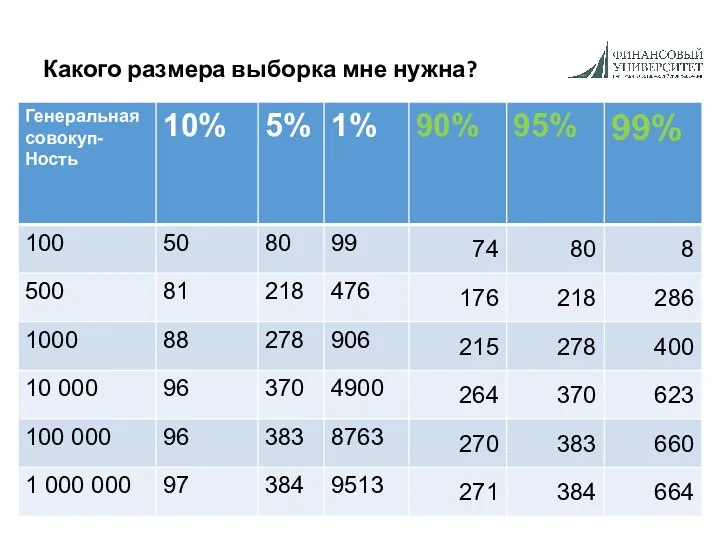
Какого размера выборка мне нужна?

Процент людей, заполнивших бланк полученного опроса, называют «процентной долей ответивших».
Процентная доля ответивших прямым образом зависит от ряда факторов, таких как отношения с целевой аудиторией, продолжительность и сложность опроса, предлагаемые поощрения и тема опроса.
Для онлайн-опросов, в которых с получателями предварительно не были установлены отношения, процентная доля ответивших в 20-30% считается очень высокой.
Более консервативным и вероятным является значение 10-14%, если Вы до этого не проводили опрос в данной совокупности.
Насколько отзывчивыми окажутся люди?

Если нужно, чтобы опрос заполнили 100 женщин, пользующихся шампунем, и Вы считаете, что 10% женщин, которым Вы отправили опрос, его заполнят, требуется отослать опрос 1000 женщин (100/10%)!
Скольким людям отсылать опрос (применимо для почтовых, интернет-опросов по email и в социальных сетях)?

N t2 pq
n= —————-
N Dp2 + tpq
N – размер генеральной совокупности;
p и q – выборочные доли (например, мужчины и женщины), их значение можно для надежности взять равным по 0.5, так как при этом их произведение максимально.
Если долей больше двух и их сумма равна единице, то и произведение уменьшается на порядок с учетом нового деления;
Dp – допустимая погрешность или ошибка выборки, обычно равна 5% или 0.05 (наиболее часто используют значения 0.01; 0.03; 0.05).
При этом доверительная вероятность Р=0.95, а t=1.96 (примерно 2)
(t – это доверительный коэффициент, который определяется по таблице стандартного нормального распределения).

7 803 000 . 0.5 . 0.5 . 22
n= ——————————————— = 400
7 803 000 . 0.05 . 0.05 + 2 . 0.5 . 0.5
Пример. Нужно рассчитать объем выборки для обследования трудоспособного и старше населения города.
Возьмем N=7803 тыс. человек, t=2, Dp=0.05; p=0.5; q=0.5:

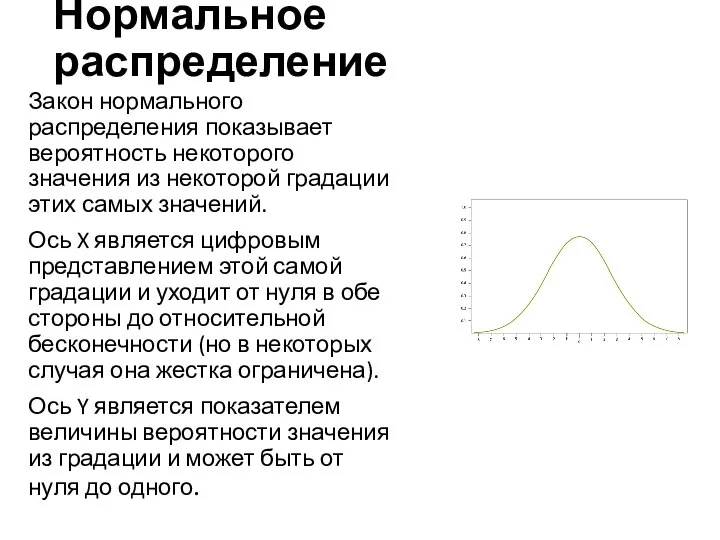
Нормальное распределение
Закон нормального распределения показывает вероятность некоторого значения из некоторой градации этих самых значений.
Ось X является цифровым представлением этой самой градации и уходит от нуля в обе стороны до относительной бесконечности (но в некоторых случая она жестка ограничена).
Ось Y является показателем величины вероятности значения из градации и может быть от нуля до одного.

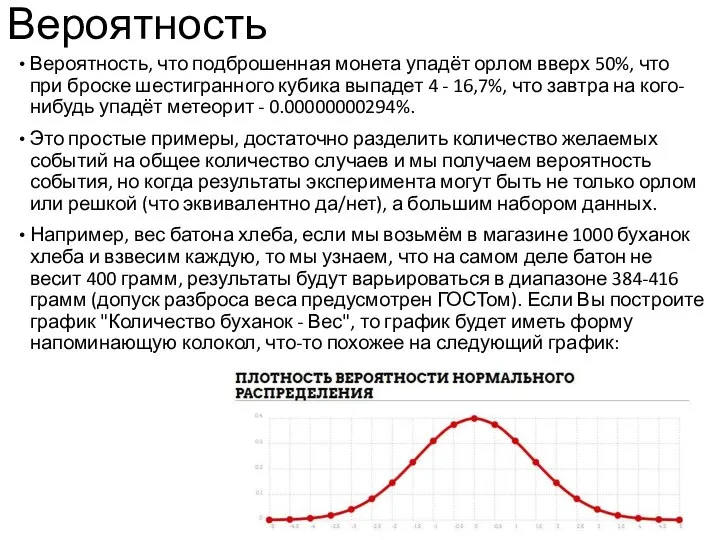
Вероятность
Вероятность, что подброшенная монета упадёт орлом вверх 50%, что при броске шестигранного кубика выпадет 4 - 16,7%, что завтра на кого-нибудь упадёт метеорит - 0.00000000294%.
Это простые примеры, достаточно разделить количество желаемых событий на общее количество случаев и мы получаем вероятность события, но когда результаты эксперимента могут быть не только орлом или решкой (что эквивалентно да/нет), а большим набором данных.
Например, вес батона хлеба, если мы возьмём в магазине 1000 буханок хлеба и взвесим каждую, то мы узнаем, что на самом деле батон не весит 400 грамм, результаты будут варьироваться в диапазоне 384-416 грамм (допуск разброса веса предусмотрен ГОСТом). Если Вы построите график "Количество буханок - Вес", то график будет иметь форму напоминающую колокол, что-то похожее на следующий график:

Такую форму график получит потому, что большинство значений близко к 400.
Это - пример нормального распределения. Множество событий имеют закон нормального распределения, например, вес или рост для определённого возраста, или среднее время Вашего похода до магазина и многие другие события также подчиняются закону нормального распределения.
В случае таблицы Вы имеете дело с дискретными данными, т.е. для каждого веса есть определённая вероятность, но в случае графика дело немного меняется, теперь мы говорим не о 1000 буханок, которые мы взвесили, а обо всех буханках в мире сразу!
Зачем?
Что бы не взвешивать все буханки.
Имея закон распределения, который мы получили взвесив 1000 буханок (мы могли взвесить 100, 200, 500, сколько угодно), мы можем предположить, что сколько бы мы буханок не взяли, замерив их, мы получим ту же форму колокола.
Используя термины статистики, все буханки хлеба - это генеральная совокупность, 1000 замеренных буханок - выборка.

Теперь, возьмём одну буханку хлеба, какова вероятность, что её вес будет между 390г и 400г?
Вероятность события между a и b:
P(a ≤ X ≤ b) = P(X ≤ b) - P(X ≤ a)
Распределение вероятности - это функция, в которой для каждого события Х присваивается вероятность p, что событие произойдёт

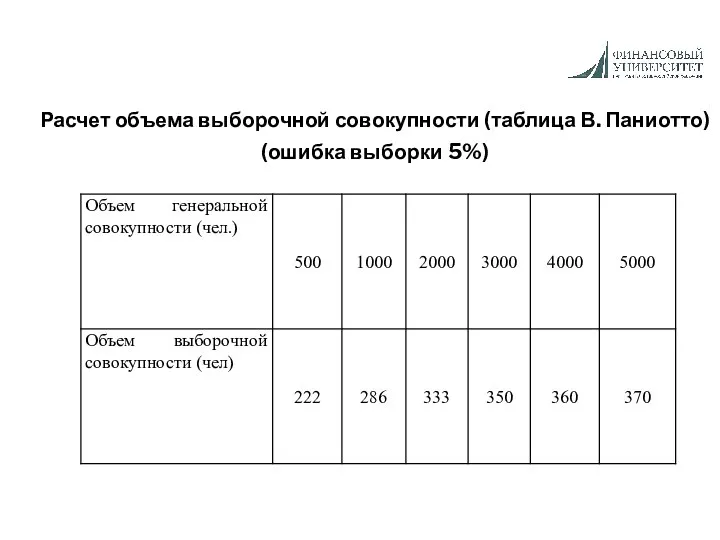
Расчет объема выборочной совокупности (таблица В. Паниотто)
(ошибка выборки 5%)

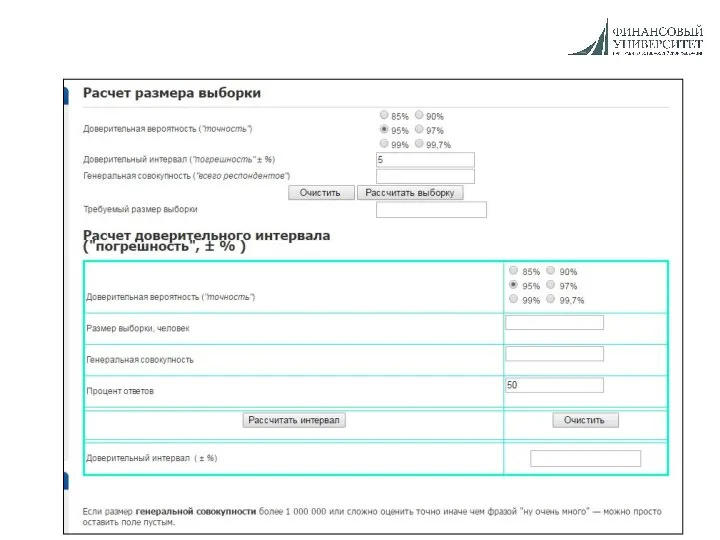
Сайт пермских социологов https://socioline.ru/rv.php

https://www.bma.ru/kalkulyator-vyborki/?lang=ru

Логическая схема обработки и анализа информации – краткое описание алгоритма действий исследователя в процессе математической и логической обработки полученной базы данных.
ГИПОТЕЗА
Основная функция гипотезы состоит в получении новых научных высказываний, совершенствуют или обогащают имеющиеся знания.
Отличается научная гипотеза тем, что новые высказывания можно назвать научными гипотезами в том случае, если они,
во-первых, составляют научный вывод из доказанных положений,
во-вторых, составляют высказывания, получении путем научных выводов с целью объяснения соответствующего явления;
в-третьих, абстрагированные на эмпирических данных и подтверждены практикой или руководствами в соответствующей теорией.
Научная гипотеза, и в том ее сила, может быть сформулирована только в результате предварительного анализа объекта.

Известный социолог Макс Роберт Коэн как-то в шутку заметил: «Гипотезы возникают у людей, которые думают».
Иногда возникает вопрос: стоит ли вести исследования, если утверждение гипотезы и без того известно?
Да, стоит, потому что сознание не может дать обоснованного ответа на многие вопросы.
Другим источником построения гипотез может выступать аналогия. Метод давно известен в науке.
Суть метода аналогии заключается в том, что полученные знания при исследовании какого-либо объекта применяются на другой, менее изученный, менее доступен.
Необходимо помнить, что выводы, полученные по аналогии, чаще всего правдоподобные.

Вариант логической схемы анализа и обработки информации
• для вопросов №27, 29 разработать интервальную шкалу для более эффективной обработки информации;
• вопросы № 9, 12, 21, 27-31 нуждаются в предварительной смысловой обработке открытой части вопросов;
• Простые распределения ответов на все вопросы анкеты;
• Связи (перекрестные таблицы) для подтверждения гипотез:
Гипотеза 1 – 12х10, 12х16, 12х19, 12х20, 12х21, 12х22, 12х24, 12х26, 31х10, 31х18.
Гипотеза 2 – 24х16, 24х17, 24х18, 24х19, 24х20, 24х21, 24х22.
Гипотеза 3 – (28 + 29)х7, 8, 16, 17, 18, 19, 20, 21, 24, 26.
• Индексирование признаков: 10х7х8; 19х7х8; 24х7х8; 26х7х8.

ЗАДАНИЕ
Определите 3 гипотетических темы исследования (Например, отношение населения к изменению Конституции)
Рассчитайте выборочную совокупность для проведения опроса в трех разных по количеству населения городах России.
Разработайте логическую схему обработки и анализа информации самостоятельного социологического исследования.
Выдвиньте гипотезы вашего исследования (3-4 шт)
Составьте перечень смысловых блоков анкеты. Определите логику размещения блоков в анкете.

Темы выступлений на следующее занятие:
Информирование:
По социальным проблемам современной России
По политическим проблемам современной России
По международным проблемам
Доклады:
Классификация неопросных социологических методов изучения общественного мнения.
Роль наблюдателя при проведении исследования общественного мнения.

Задание на самостоятельное изучение темы:
Знать, как рассчитывается выборка социологического опроса.