АЛГЕБРАИЧЕСКИЙ ПОДХОД К ИНТЕЛЛЕКТУАЛЬНОЙ ОБРАБОТКЕ ДАННЫХ И ЗНАНИЙ д. ф.-м. н. Кулик Борис Александрович, к. т. н. Зуенко Александр А

План доклада
1. Логический анализ: алгебраический подход и теория формальных систем (ТФС)
2. Алгебра кортежей (АК): основные определения
3. Представление в АК основных видов данных и знаний
4. Новые возможности логического анализа в АК
5 Семантический анализ информации
6. Методы снижения трудоемкости в АК
7. Метрические аспекты АК
8. Выводы

Моделирование логики рассуждений (методы логического анализа)
Силлогистика Аристотеля, до начала XIX века

Столкновение подходов к логическому анализу
(эра компьютерной техники)

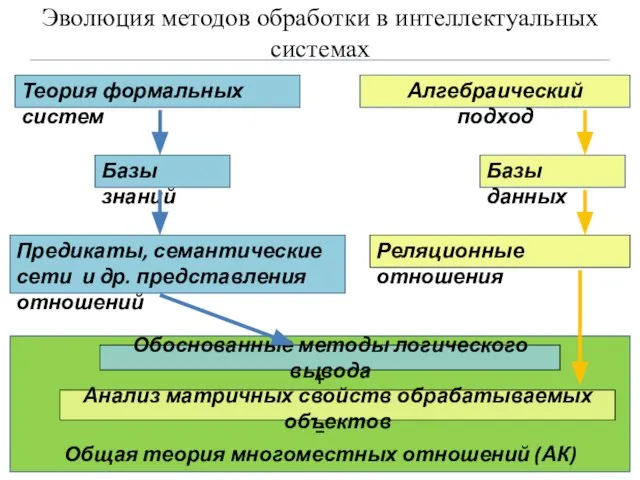
Эволюция методов обработки в интеллектуальных системах
Теория формальных систем
Алгебраический подход
Базы знаний
Базы данных
Реляционные отношения
Предикаты, семантические сети и др. представления отношений

Сравнение формального и алгебраического подходов
Формальный подход
Алфавит.
Синтаксические правила.
Аксиомы.
Правила вывода.
Алгебраический подход
Носитель.
Совокупность операций и отношений
Основные законы, связывающие операции и отношения
Известны математические объекты, которые можно представить и как формальные и как алгебраические системы, например,
булева система – булева алгебра;
кольцо;
решетка и т.д.

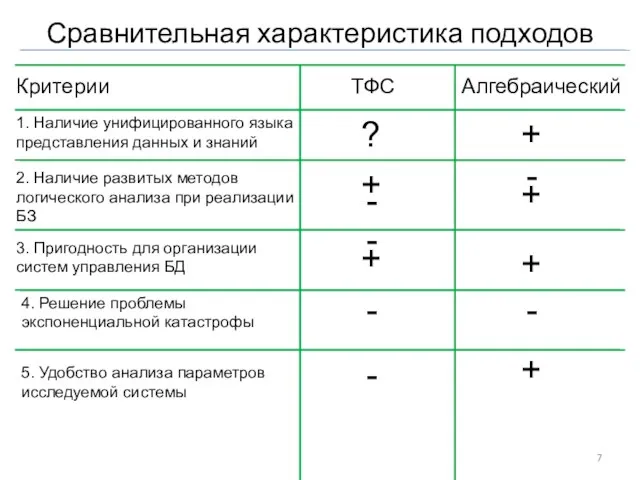
Сравнительная характеристика подходов
ТФС
Алгебраический
Критерии
1. Наличие унифицированного языка представления данных и знаний
?
+
2. Наличие развитых методов логического анализа при реализации БЗ
+
3. Пригодность для организации систем управления БД
+
4. Решение проблемы экспоненциальной катастрофы
-
-
5. Удобство анализа параметров исследуемой системы
-
+
-

План доклада
1. Логический анализ: алгебраический подход и теория формальных систем (ТФС)
2. Алгебра кортежей (АК): основные определения
3. Представление в АК основных видов данных и знаний
4. Новые возможности логического анализа в АК
5 Семантический анализ информации
6. Методы снижения трудоемкости в АК
7. Метрические аспекты АК
8. Выводы

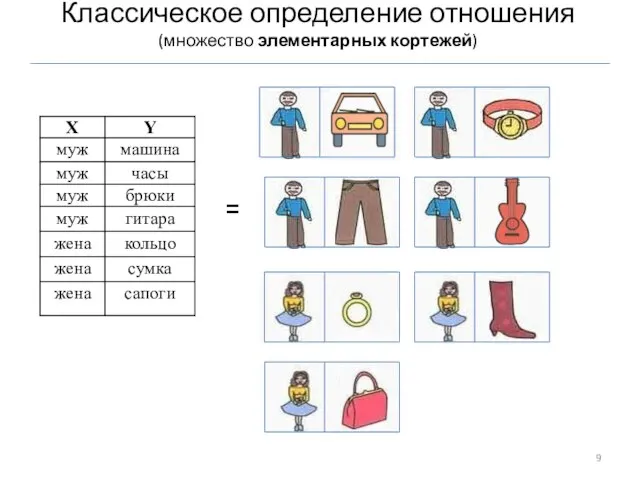
Классическое определение отношения
(множество элементарных кортежей)
=

=
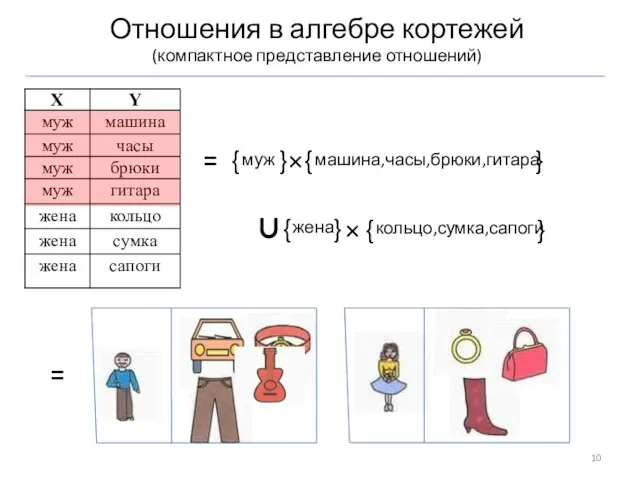
Отношения в алгебре кортежей
(компактное представление отношений)
=

Определение алгебры кортежей
Алгебра кортежей (АК) – это алгебраическая система.
Носитель АК: произвольная совокупность многоместных отношений, определенных в одном гибком универсуме и выраженных в специфических структурах:
C‑кортеж;
C-система;
D-кортеж;
D‑система.
называемых АК-объектами.
Каждый АК-объект можно интерпретировать как множество элементарных кортежей.
Операции АК:
операции алгебры множеств (∩, ∪ , \ ) и дополнение (− )
операции с атрибутами:
переименование атрибута;
перестановка атрибутов;
добавление нового фиктивного атрибута (+Atr);
элиминация атрибута (−Atr).
Отношения алгебры множеств: ∈, ⊆ , = .
Производные операции: соединение (⊕) и композиция (∙) отношений
Обобщенные операции и отношения (∩G, ∪G, \G , ⊆G, = G )

Первая особенность АК: компактное представление
отношений (С-кортеж)
C-кортеж
R[XY...Z] = [A B ... C], где
A, B, ..., C – компоненты C-кортежа;
A ⊆ X, B ⊆ Y, ..., C ⊆ Z, т.е. подмножества доменов соответствующих атрибутов.
Интерпретация – декартово произведение множеств:
R[XY...Z] = [A B ... C] = A×B× ... ×C.
Пример:
R [XY...Z] = [{a,c} {c,d,f} {b}] = {a,c} × {c,d,f} × {b} =

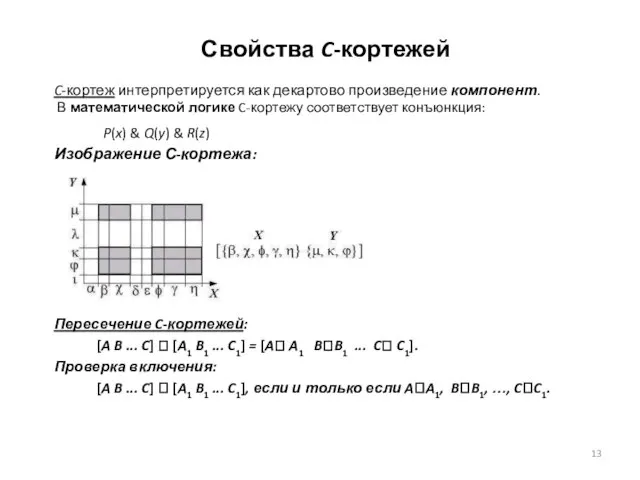
Свойства C-кортежей
C-кортеж интерпретируется как декартово произведение компонент.
В математической логике C-кортежу соответствует конъюнкция:
P(x) & Q(y) & R(z)
Изображение С-кортежа:
Пересечение C-кортежей:
[A B ... C]  [A1 B1 ... C1] = [A A1 BB1 ... C C1].
Проверка включения:
[A B ... C]  [A1 B1 ... C1], если и только если AA1, BB1, …, CC1.

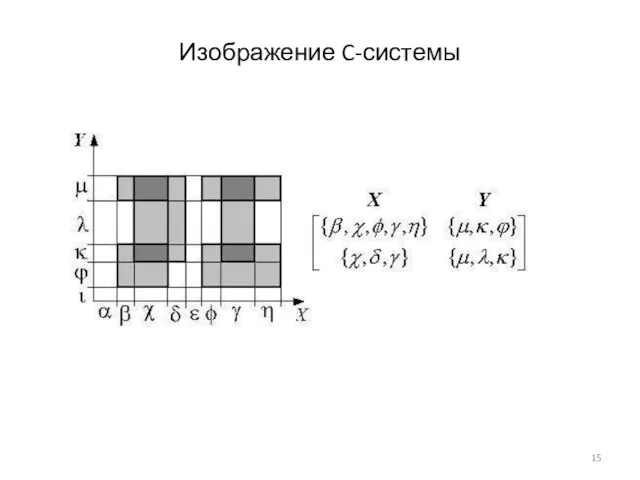
C-система -- это объединение C-кортежей с одинаковой схемой отношения.
Пример:
В математической логике C-кортежу [P Q R ] соответствует конъюнкт P(x) & Q(y) & R(z), где P(x), Q(y) , R(z) – некоторые предикаты, а P, Q, R – множества их выполняющих подстановок.
C-системе можно сопоставить ДНФ:
⇔ (P1(x) & Q1(y) & R1(z)) ∨ (P2(x) & Q2(y) & R2(z)) .
Первая особенность АК: компактное представление отношений (С-система)

Изображение C-системы

Полная компонента – “*” равна домену соответствующего атрибута. Используется в C‑кортежах и C-системах.
Пустая компонента - “∅” используется в D-кортежах и
D-системах
Например, для X = {a, b, c, d}, Y = {f, g, h}, Z={a, b, c}:
Q[XYZ] = [* {f, g} {a, c}] = [{a, b, c, d} {f, g} {a, c}] - здесь “*” – это множество, равное домену атрибута X.
Если T = [{b, d} * {a, b}], то = ]{a, c} ∅ {c}[.
Пусть A – произвольная компонента атрибута X, а * - его полная компонента. Тогда
А ∩ * = A;
A ∪ * = * ;
= ∅;
= *.
Первая особенность АК: компактное представление
отношений (фиктивные компоненты)

Дополнение C-кортежа:
D-кортеж – сокращенное обозначение диагональной C‑системы.
В математической логике D-кортежу ]P Q R[ в схеме отношения [XYZ] соответствует дизъюнкция: P(x) ∨ Q(y) ∨ R(z).
Дополнением C-кортежа [ {β, χ, φ, γ, η} {μ, κ, ϕ} ] является D-кортеж
] {α, δ, ε} {ι, λ} [ (на схеме не закрашен)
или C-система
Вторая особенность АК: операция дополнения отношений (D-кортеж)

R = ,
В математической логике D-системе соответствует КНФ.
В частности, дополнением C-кортежа
Q[XYZ] = [A * C]
является D-кортеж
[XYZ] = ] ∅ [
Вторая особенность АК: операция дополнения отношений (D-система)
Дополнение C-системы ( ) - это пересечение D-кортежей с идентичными схемами отношений.
На рисунке C-система R закрашена,
а D-система не закрашена.

Операции с атрибутами
Переименование атрибутов (только для атрибутов одного сорта).
Перестановка атрибутов – эквивалентное преобразование АК-объекта).
Добавление фиктивного атрибута (+Atr) – равносильное по смыслу преобразование при условии, что добавляемый атрибут не содержится в схеме отношения данного АК-объекта.
Соответствует правилу обобщения исчисления предикатов:
из формулы A выводимо ∀x(A)
(при условии, что x не является свободной переменной в A)
4. Элиминация атрибута (– Atr) – интерпретирует операции навешивания кванторов в исчислении предикатов.
Пусть TC – С-кортеж или C-система, а TD – D-кортеж или D-система, содержащие атрибут X. Тогда
–X(TC) равносильно ∃x(TC);
–X(TD) равносильно ∀x(TD).
Третья особенность АК: работа с отношениями, заданными в разных декартовых произведениях

Перестановка атрибутов
Добавление фиктивного атрибута
Элиминация атрибута
Третья особенность АК: работа с отношениями, заданными в разных декартовых произведениях
(примеры операций с атрибутами)

Третья особенность АК: работа с отношениями, заданными в разных декартовых произведениях
(некоторые производные операции )
Пусть заданы две структуры R1[V] и R2[W].
Здесь V и W являются множествами атрибутов и V ≠ W. Эти множества можно разложить на непересекающиеся подмножества X, Y, Z с помощью следующих операций:
X = W\V; Y = W∩V; Z = V\W. Тогда V = Y ∪ Z и W = X∪Y.
С учетом этого данные отношения можно переписать так:
R1[V] = R1[YZ] и R2[W] = R2[XY].
Операция соединения: R1[YZ] ⊕ R2[XY] = +X(R1) ∩ +Z(R2) = ∀x(R1) ∩ ∀z(R2).
Операция композиции: R1[YZ] ° R2[XY] = –Y(+X(R1) ∩ +Z(R2)) = –Y(R1 ⊕ R2) =
= ∃y(∀x(R1) ∩ ∀z(R2)).
Q[YZ] =
P[XY] =
Схемы отношений у P и Q разные,
но их можно привести к одной
Q1[XYZ] = ∀x(Q[YZ]) =
Вычислив их пересечение, получим соединение отношений
P1[XYZ] = ∀z(P[XY]) =
P⊕Q =

Назовем операции алгебры множеств с АК‑объектами с предварительным добавлением недостающих фиктивных атрибутов обобщенными операциями и отношениями алгебры множеств в АК и обозначим их соответственно
, , , , и т.д.
Примером обобщенной операции является соединение отношений
P[XY] ⊕ Q[YZ] = +Z(P[XY]) ∩ +X(Q[YZ]) то же самое, что
P[XY] ∩G Q[YZ].
Введение обобщенных операций и отношений позволяет определить алгебру отношений с произвольным составом атрибутов как алгебру множеств.
Третья особенность АК: работа с отношениями, заданными в разных декартовых произведениях
(обобщенные операции и отношения)
∩ G
=
[{a},{b,d}]
∩ G
[{a},{k,l}]
X Y
X Z
=
[{a},{b,d},*]
X Y Z
∩
[{a},*,{k,l}]
=
X Y Z
=
[{a},{b,d},{k,l}]
X Y Z
=

Гибкий универсум
Пусть X1, X2, …, Xn – множество атрибутов. Тогда
X1 × X2 × … × Xn – пространство атрибутов или универсум;
[Xi Xj … Xk] (i, j, …, k ∈ 1 ÷ n) – схема определенного отношения;
Xi × Xj × … × Xk – частный универсум;
Гибкий универсум – это произвольная совокупность частных универсумов для системы, определенной на пространстве
X1 × X2 × … × Xn.
Однотипные АК-объекты - разные АК-объекты с одной и той же схемой отношения.
Интерпретация
Частный универсум Xi × Xj × … × Xk
в исчислении предикатов соответствует
общезначимой формуле F(xi, xj, …, xk),
где xi, xj, …, xk – переменные, областями значений которых являются домены атрибутов Xi Xj … Xk.
Таким образом, совокупность частных универсумов в АК соответствует классу общезначимых формул в исчислении предикатов.

Основные теоремы АК
(здесь нумерация теорем в соответствии с представляемой ниже книгой)
Теорема 2.1. Алгебра кортежей для однотипных АК-объектов изоморфна алгебре множеств
Пусть заданы однотипные C-кортежи P = [P1 P2 … Pn] и Q = [Q1 Q2 … Qn].
Теорема 2.2. P ∩ Q = [P1∩Q1 P2∩Q2 … Pn∩Qn].
Примеры: [{b, d} {f, h} {a, b}] ∩ [ * {f, g} {a, c}] = [{b, d} {f} {a}];
[{b, d} {f, h} {a, b}] ∩ [ * {g} {a, c}] = [{b, d} ∅ {a}] = ∅.
Теорема 2.3. P ⊆ Q, если и только если Pi ⊆ Qi для всех i = 1, 2, …, n.
Теорема 2.4. P ∪ Q ⊆ [P1∪Q1 P2∪Q2 … Pn ∪ Qn], причем равенство возможно лишь в двух случаях:
P ⊆ Q или Q ⊆ P;
Pi = Qi для всех соответствующих пар компонент, за исключением одной пары.
Теорема 2.7. Для произвольного C-кортежа P = [P1 P2 … Pn] его дополнение равно D-кортежу = ] … [.
Часть теорем АК (всего 30 теорем) предусматривают выполнение операций алгебры множеств с однотипными АК-объектами. Для работы с АК-объектами, имеющими разные схемы отношений, вводятся операции с атрибутами.

План доклада
1. Логический анализ: алгебраический подход и теория формальных систем (ТФС)
2. Алгебра кортежей (АК): основные определения
3. Представление в АК основных видов данных и знаний
4. Новые возможности логического анализа в АК
5 Семантический анализ информации
6. Методы снижения трудоемкости в АК
7. Метрические аспекты АК
8. Выводы

Моделирование графов
Пример вычисления степени графа
G2[XY] = G [XY] ∙ G [XY] = −Y(G[XY]⊕ G[YZ]) :
Сначала вычисляем соединение графа с собой:
∩ =
Затем элиминируем атрибут Y:
G2 =
Транзитивное замыкание графа G, содержащего n вершин, можно построить с помощью следующей последовательности операций:
G+ = G ∪ G2∪ G 3 … ∪ G k, где k ≤ n.
…
G[XY] =

Семантические сети
Исходная сеть Правило и факты Результат
R1[XY] = R2[XY] =
R3[XY] = [{K} {L}]; R4[XY] = [{A} {A}].
Левая часть правила:
(R1[XY] ∩ [{D} *]) ⊕ (R2[YZ] ∩ [* {K}]) =
= [{D} {F, G, H} {K}] .
Правая часть правила:
[{F, G, H} {M}] .

Экспертные системы
Базы знаний экспертных систем (ЭС) содержат модели и правила. Известно четыре типа моделей: логические модели, предикаты, семантические сети и фреймы. Рассмотрим предикаты и правила.
Предикаты по сути являются отношениями или элементами отношений. Например, набор предикатов ЭС
isa(a1, S1); isa(a2, S1); isa(a3, S1); isa(a4, S2);
prop(S1, c1, d1); prop(S1, c2, d2); prop(S2, c1, d3).
является представлением двух отношений: бинарного isa и трехместного prop. В структурах АК предикаты можно выразить как
C-системы:
isa[XY] = ; prop[YZV] =
Пусть задано следующее правило вывода:
ЕСЛИ isa[XY] И prop[YZV] ТО property[XZV]
и факты, X = a1 и V = d2, тогда мы можем выразить их в виде запроса
Q[XV] = [{a1} {d2}].
Алгоритм реализации правила с учетом фактов:
isa[XY] ∩G prop[YZV] ∩G Q[XV].

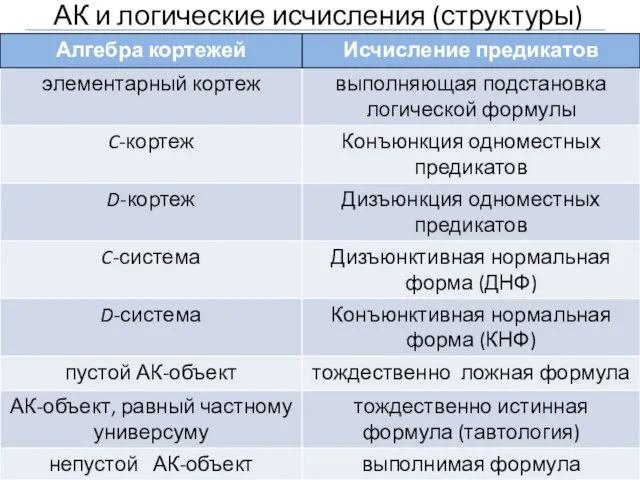
АК и логические исчисления (структуры)

АК и логические исчисления (операции)

План доклада
1. Логический анализ: алгебраический подход и теория формальных систем (ТФС)
2. Алгебра кортежей (АК): основные определения
3. Представление в АК основных видов данных и знаний
4. Новые возможности логического анализа в АК
a) проверка правильности следствия
b) генерация возможных следствий
с) поиск абдуктивных заключений
5 Семантический анализ информации
6. Методы снижения трудоемкости в АК
7. Метрические аспекты АК
8. Выводы

Новый подход к логическому выводу
(методы АК)
Существующие системы логического вывода:
исчисления гильбертовского типа (Д. Гильберт и В. Аккерман)
натуральное исчисление (Г. Генцен)
принцип резолюции (М. Девис и Х. Патнем )
Теорема 1. Пусть даны формулы F1, ..., Fn и формула G. Тогда G есть логическое следствие F1, ..., Fn тогда и только тогда, когда формула
((F1 ∧ ... ∧ Fn) ⊃ G) общезначима.
Теорема 2. Пусть даны формулы F1, ..., Fn и формула G. Тогда G есть логическое следствие F1, ..., Fn тогда и только тогда, когда формула
(F1 ∧ ... ∧ Fn ∧ ¬G) противоречива.
Логический вывод в АК:
Метод 1. Пусть даны АК-объекты F1, ..., Fn и G. Тогда G есть следствие
F1, ..., Fn тогда и только тогда, когда
(F1 ∩G ... ∩G Fn) ≠∅ и (F1 ∩G ... ∩G Fn) ⊆ GG.
Метод 2. Пусть даны АК-объекты F1, ..., Fn и G. Тогда G есть следствие F1, ..., Fn тогда и только тогда, когда
(F1 ∩G... ∩G Fn) ≠∅ и F1 ∩G ... ∩G Fn ∩G = ∅.

Новый подход к логическому выводу
(интерпретация логического вывода )
Теорема 4.1. Если для логических формул A и B имеется интерпретация в виде множеств SA и SB, то общезначимость импликации A ⊃ B равносильна выполнению отношения SA ⊆ SB.
Семантика следствия
Предлагаемый подход позволяет по новому осмыслить суть логического следования в классической логике. Известно, что справедливость отношения A ⊆ B означает, что B является необходимым условием или свойством A.
Из соотношения (1) ясно, что логическое следствие является корректным не только потому, что получено на основе правил вывода, смысл которых не всегда понятен, но еще и потому, что является необходимым условием существования антецедента.

Новый подход к логическому выводу
(типы задач)
Пусть задана система аксиом (посылок) A1, A2, …, An и возможное следствие B.
Два типа задач:
1) Задача проверки правильности следствия. Процедура доказательства производится как проверка правильности обобщенного включения
(A1 ∩G … ∩G An) ⊆G B.
2) Задача вывода следствий с учетом ограничений. Для решения этой задачи сначала вычисляется АК-объект A = A1 ∩G … ∩G An, после чего производится выбор таких Bi, для которых соблюдается A ⊆G Bi.
К ограничениям относятся состав и возможное число атрибутов в следствии
Для вывода возможных следствий в АК используется следующий алгоритм
Преобразовать АК-объект A = A1 ∩G … ∩G An в C-систему.
Выбрать из A некоторую совокупность неполных проекций (для любой проекции Pi(A) справедливо A ⊆ G Pi(A) ).
Сформировать с учетом ограничений проекции, содержащие хотя бы одну неполную проекцию.
Для АК-объектов, полученных на предыдущих шагах, построить покрывающие их
АК-объекты.
Любой АК-объект, полученный на шагах 1-4, является следствием.

Новый подход к логическому выводу
(проверка правильности следствия: пример)
Задача: Проверить корректность правила дилеммы
Решение:
Верхняя часть правила методами АК преобразуется в C-систему
Up[ABC] = ,
нижняя часть правила равна C-кортежу
Down[C] = [{1}]
или после добавления фиктивных атрибутов
Down[ABC] = [ * * {1}]
Проверка показывает, что Up[ABC] ⊆G Down[C].

Новый подход к логическому выводу
(вывод следствий: пример)
Задача: Вывести из заданной системы посылок все следствия с учетом ограничений на состав переменных
Решение:
Система посылок представима в виде С-системы
Up[ABC] = ,
Здесь полными являются только проекции: [XA] и [XB], так как содержат все значения атрибутов.
Ответ:

Задача о преступлении
Карабас-Барабас: “Я совершил это, Папа Карло не виноват”
Папа Карло: “Карабас-Барабас не виноват, Преступление совершил Кот Базилио”
Кот Базилио : “Я не виноват, виноват Карабас-Барабас ”
Правду говорит только один, остальные лгут. Кто преступник?
Карабас-Барабас: P1[ABC] = P11 ∩ P12 = [{1} * *] ∩ [* {0} *] = [{1} {0} *] ;
Папа Карло: P2[ABC] = P21 ∩ P22 = [{0} * *] ∩ [* * {1}] = [{0} * {1}] ;
Кот Базилио: P3[ABC] = P31 ∩ P32 = [* * {0}] ∩ [{1} * *] = [{1} * {0}].
На естественном языке:
На языке АК:
Гипотезы:

Задача о преступлении
Гипотеза 1 (Карабас-Барабас – честный) :
Гипотеза 2 (Папа Карло – честный) :
Гипотеза 3 (Кот Базилио – честный) :
Гипотеза отвергается
Виновен Кот Базилио, честный – Папа Карло, а чиновник – Карабас-Барабас.
Гипотеза отвергается

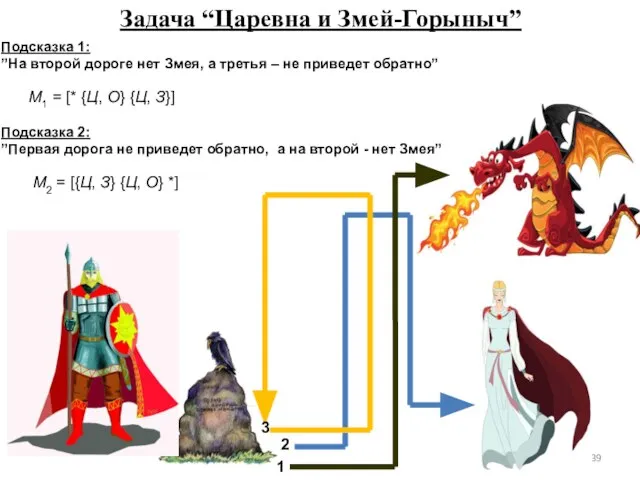
Задача “Царевна и Змей-Горыныч”
Подсказка 1:
”На второй дороге нет Змея, а третья – не приведет обратно”
Подсказка 2:
”Первая дорога не приведет обратно, а на второй - нет Змея”
1
2
3
M1 = [* {Ц, О} {Ц, З}]
M2 = [{Ц, З} {Ц, О} *]

Задача “Царевна и Змей-Горыныч”
К царевне ведет вторая дорога
Гипотеза 1 (первое утверждение верно, а второе - нет) :
Гипотеза 2 (второе утверждение верно, а первое - нет) :
К царевне ведет вторая дорога

Задача о турнире волшебников
Гарри (A)
Рон (B)
Гермиона (С)
Драко (D)
Судья: В каждом заявлении одно высказывание истинное, а другое – ложное.

Задача о турнире волшебников
С учетом замечаний судьи, посылки примут вид:
∩
[* {2} * *]
=
∪
[{1} * * *]
∩
=
=
P1=
P2=
P3=
Ответ: 1-й - Гарри, 2-й - Драко, 3-я – Гермиона, 4-й – Рон.

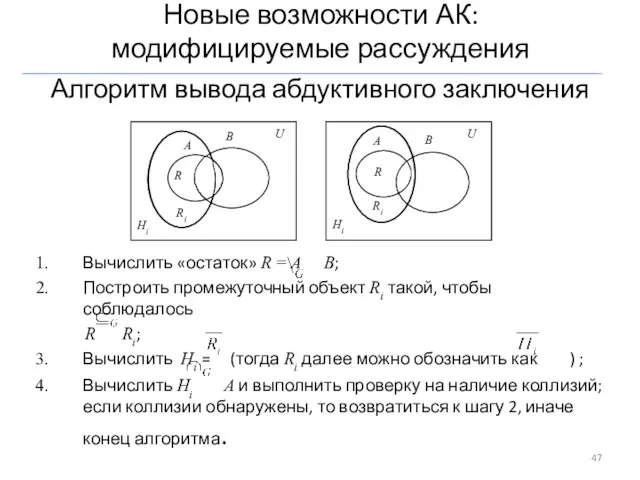
Коллизии
Коллизии – это ситуации, которые возникают в модифицируемых рассуждениях при вводе новых знаний (гипотез) и распознаются как нарушение некоторых формально выраженных правил или ограничений, регулирующих целостность или смысловое содержание системы.
Виды коллизий в системах типа силлогистики:
парадокса, когда из посылок следует суждение типа "всем A не присуще A" (A ⊃ ) и, значит, объем термина A пустой;
цикла, когда в системе множеств выводится соотношение A ⊆ В ⊆ … ⊆ A, что означает эквивалентность терминов, входящих в данный цикл;
неадекватности, когда следствия системы рассуждений не соответствуют бесспорным фактам или обоснованным утверждениям.

Коллизии в системах типа силлогистики: пример
Даны посылки:
1. Все мои друзья хвастуны и не скандалисты
2. Все хвастуны не уверены в себе.
3. Все не скандалисты уверены в себе.
Необходимо проанализировать посылки на наличие коллизий
Из заданных посылок следует утверждение
"Все мои друзья не мои друзья",
показывающее, что множество моих друзей пусто (коллизия парадокса).
Полученный может вывод не соответствовать действительности – коллизия неадекватности

Коллизии в системах типа силлогистики:
решение примера

Коллизии (продолжение)
Коллизии в системах, выходящих за рамки силлогистики
1)"вырождение" атрибутов - значимые атрибуты равны пустому множеству (в полисиллогистике - коллизия парадокса);
2) при вводе новых знаний различные атрибуты становятся тождественными по составу элементов, что противоречит семантике системы (в полисиллогистике – колизия цикла);
3) несоответствие полученных результатов с достоверными фактами или обоснованными утверждениями (в полисиллогистике - коллизия неадекватности);
4) несоответствие полученных результатов с трудноформализуемыми ограничениями, описанными в постановке задачи (например, « в кортеже не должно быть одинаковых значений»).
5) ситуации, которые используются для обоснования правомерности применения немонотонных логик, например:
"все птицы летают”;
"страус Тити птица, но не летает"

Алгоритм вывода абдуктивного заключения
Вычислить «остаток» R = A B;
Построить промежуточный объект Ri такой, чтобы соблюдалось
R Ri;
Вычислить Hi = (тогда Ri далее можно обозначить как ) ;
Вычислить Hi A и выполнить проверку на наличие коллизий; если коллизии обнаружены, то возвратиться к шагу 2, иначе конец алгоритма.
A
Новые возможности АК:
модифицируемые рассуждения

Новые возможности АК:
пример 1
Восстановим недостающую посылку в правиле дилеммы
Пусть даны 2 посылки A → C и A ∨ B и следствие C. Необходимо найти недостающую посылку, чтобы следствие выводилось. Преобразуем формулы в структуры АК.
A → C соответствует P1[XA XB XC] = .
A ∨ B соответствует P2[XA XB XC] = .
C соответствует B[XA XB XC] = [ * * {1}].
Используем алгоритм.
R = (P1∩P2)\B = P1∩P2 ∩ = [{0} {1} {0}].
Выберем проекцию [ XB XC] (такого сочетания нет в посылках), получим
Ri [ XB XC] = [{1} {0}]; [ XB XC] = ]{0} {1}[,
что соответствует формуле B → C .

Новые возможности АК:
пример 2
База знаний диагностики автомобиля [Д.А. Страбыкин, Н.М. Томчук]
Если из выхлопной трубы ЧЕРНЫЙ ДЫМ, то БОГАТАЯ СМЕСЬ или РАННЕЕ ЗАЖИГАНИЕ.
x6 ⊃ (x2 ∨ x3).
Если СИНИЙ ДЫМ, то ПОВЫШЕННЫЙ РАСХОД МАСЛА.
x7 ⊃ x5.
Если выхлопная ТРУБА ЧЕРНАЯ, то БОГАТАЯ СМЕСЬ или РАННЕЕ ЗАЖИГАНИЕ или ПОВЫШЕННЫЙ РАСХОД МАСЛА.
x1 ⊃ (x2 ∨ x3∨ x5)
Если ПОВЫШЕННЫЙ РАСХОД МАСЛА, то ИЗНОС МАСЛОСЪЕМНЫХ КОЛПАЧКОВ или ИЗНОС ПОРШНЕВЫХ КОЛЕЦ или ИЗНОС ЦИЛИНДРОВ.
x5 ⊃ (x8 ∨ x9∨ x10)
Если НОРМАЛЬНАЯ КОМПРЕССИЯ, то нет ИЗНОСА ПОРШНЕВЫХ КОЛЕЦ и нет ИЗНОСА ЦИЛИНДРОВ
x4 ⊃ (¬x9 ∧ ¬x10)
Заключение: Если НОРМАЛЬНАЯ КОМПРЕССИЯ и выхлопная ТРУБА ЧЕРНАЯ и СИНИЙ ДЫМ, то ИЗНОС ПОРШНЕВЫХ КОЛЕЦ.
(x3 ∧ x1 ∧ x7) ⊃ x9

Продолжение примера 2
Эту БЗ можно представить как КНФ
A =
которую преобразуем в D-систему
Заключение выразим как D-кортеж
B[X1 X4 X7 X9] = ]{0} {0} {0} {1}[.

Продолжение примера 2
Алгоритм «наращивания» R
1) оставить в качестве одну из неполных проекций;
2) выбрать в качестве любую проекцию при условии, что в ее состав входит, по крайней мере, одна неполная проекция;
3) для выбранного по предыдущим правилам АК-объекта построить покрывающий его неполный АК‑объект.
Доказано, что данный алгоритм предусматривает все возможные случаи «наращивания» R.

Иллюстрация алгоритма наращивания на примере 2
В качестве примера выберем проекцию [X1X9], которая после сокращений будет равна C-кортежу Ri[X1X9] = [{1} {0}]. Тогда можно сформировать следующие формулы для :
1) (соответствует C‑кортежу Ri);
2) ;
3) .
(формулы 2 и 3 соответствуют АК‑объектам, которые покрывают C-кортеж Ri)
и т.д.

План доклада
1. Логический анализ: алгебраический подход и теория формальных систем (ТФС)
2. Алгебра кортежей (АК): основные определения
3. Представление в АК основных видов данных и знаний
4. Новые возможности логического анализа в АК
5 Семантический анализ информации
6. Методы снижения трудоемкости в АК
7. Метрические аспекты АК
8. Выводы

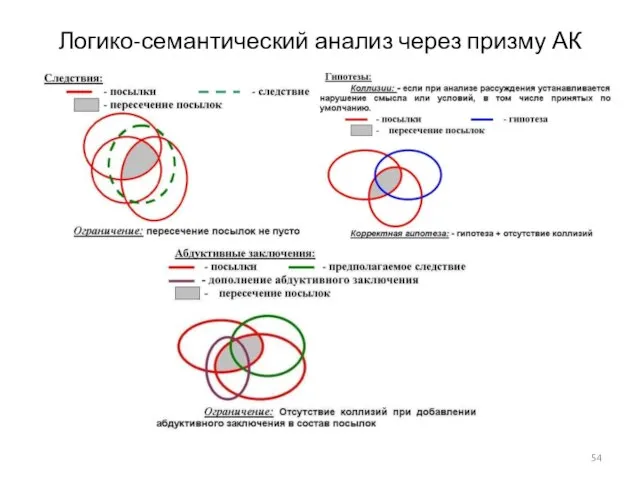
Логико-семантический анализ через призму АК

Подход к семантическому анализу на основе АК
Этапы традиционного семантического анализа:
1) отбор основополагающих понятий данной предметной области, предварительная классификация отобранных понятий;
2) дальнейшая систематизация, установление иерархических связей между некоторыми понятиями;
3) установление отношений между понятиями в рамках некоторого заранее заданного списка значимых отношений, включая специфичные для данной предметной области отношения;
4) формализация информации с использованием установленных отношений в виде семантических графов, семантических сетей, онтологий и предикатов;
5) использование языка исчисления предикатов в качестве языка семантического анализа.
Проблемы традиционного семантического анализа:
сложность совмещения логического вывода и недедуктивных (в том числе, модифицируемых) рассуждений в одной программной среде;
трудность выявления противоречий в знаниях и других нарушений ограничений целостности и/или смыслового содержания системы знаний (коллизий).

Подход к семантическому анализу на основе АК
1) отбор основополагающих понятий данной предметной области, предварительная классификация отобранных понятий;
2) дальнейшая систематизация, установление иерархических связей между некоторыми понятиями;
3) установление отношений между понятиями в рамках некоторого заранее заданного списка значимых отношений, включая специфичные для данной предметной области отношения;
4) формализация полученной на предыдущих этапах информации в структурах АК;
5) использование унифицированных методов работы с АК-объектами для решения различных задач логического, недедуктивного и предметно-ориентированного семантического анализа:
6) формализация и анализ коллизий.
Коллизии – это ситуации, которые возникают в модифицируемых рассуждениях при вводе новых знаний (гипотез) и распознаются как нарушение некоторых формально выраженных правил или ограничений, регулирующих целостность или смысловое содержание системы.

Семантика: «нелогичное» правило вывода
В семантических сетях и экспертных системах часто используют правило вывода типа
Если P1 и P2 и…и Pn, то Q.
Например, если Мать (x,y) и Родитель (y,z), то Бабушка(x,z).
В АК такие правила определены с помощью формулы
P1 ∩G P2 ∩G … ∩G Pn, ⊆ Q
По сути здесь не просто логический вывод, а создание нового отношения, смысл которого определен левой частью правила. («Бабушка – это женщина, дети которой имеют детей» или по Толковому словарю Ожегова«Мать отца или матери» -)
С учетом этого нами предложено называть такого рода правила семантическими правилами.

Вопросы и вопросно-ответные системы
Типы вопросов
1) Уточняющие вопросы или ли-вопросы:
Верно ли, что жирафы живут в Африке?
2) Восполняющие вопросы:
Кто …? Где …? Когда …? и т.д.
3) ПОЧЕМУ-вопросы
4) КАК-вопросы
5) ЗАЧЕМ-вопросы
Гетманова А.Д. Учебник по логике. М.: "Владос", 1994.
Поспелов Д. А. Моделирование рассуждений.– М.: Радио и связь, 1989.
Принципы работы вопросно-ответных систем
1) Структурирование исходной информации и вопросов к ней.
Используемые структуры: отношения (в частности, таблицы) или элементы отношений, графы, сети (семантические, по сочетаемости и т.д.), частично упорядоченные множества (в том числе решетки), правила. Все перечисленные структуры можно представить в виде отношений.
2) Формально выраженные запросы должны
легко переводиться на естественный язык ;
инициировать процедуру поиска с учетом многообразия структур подготовленной к обработке информации.

Структура вопроса
Остальные типы вопросов в стадии разработки

План доклада
1. Логический анализ: алгебраический подход и теория формальных систем (ТФС)
2. Алгебра кортежей (АК): основные определения
3. Представление в АК основных видов данных и знаний
4. Новые возможности логического анализа в АК
5 Семантический анализ информации
6. Методы снижения трудоемкости в АК
7. Метрические аспекты АК
8. Выводы

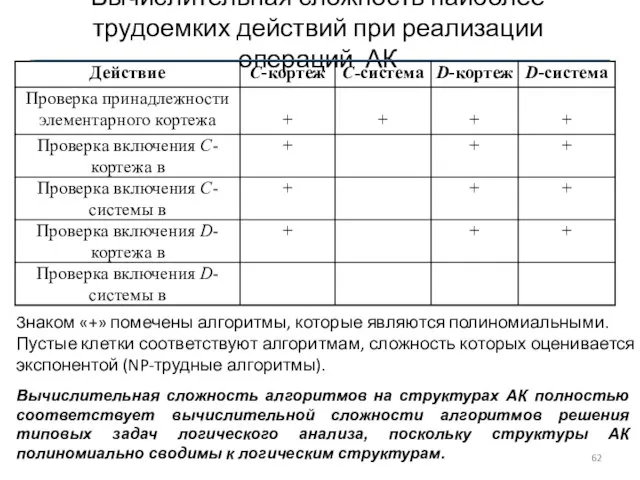
Трудоемкость операций в АК
= {a,b,c} × {b,c} × {b,c,f} ∩ {a,b,c,d} × {a,c,d} × {b,c,d} = ???
∩
1 Способ. Вычисления в элементарных кортежах
число операций = 18 × 36 × 3 = 1944
2 Способ. Вычисления в АК-объектах
C[XYZ] ∩ D[XYZ] =
= [{a,b,c} {b,c} {b,c,f}] ∩ [{a,b,c,d} {a,c,d} {b,c,d}]=
=[{a,b,c} ∩ {a,b,c,d} {b,c} ∩ {a,c,d} {b,c,f} ∩ {b,c,d}]=
= [{a,b,c} {c} {b,c}] .
число операций = 3 × 4 + 2 × 3 + 3 × 3 = 27

Вычислительная сложность наиболее трудоемких действий при реализации операций АК
Знаком «+» помечены алгоритмы, которые являются полиномиальными. Пустые клетки соответствуют алгоритмам, сложность которых оценивается экспонентой (NP-трудные алгоритмы).
Вычислительная сложность алгоритмов на структурах АК полностью соответствует вычислительной сложности алгоритмов решения типовых задач логического анализа, поскольку структуры АК полиномиально сводимы к логическим структурам.

Матричные свойства АК-объектов как средство ускорения логического вывода
Основные определения
Бесконфликтным атрибутом D-системы называется атрибут, в котором пересечение всех непустых компонент непусто.
Бесконфликтным блоком D-системы называется ее вертикальный блок, содержащий только бесконфликтные атрибуты.
Монотонным атрибутом D-системы называется бесконфликтный атрибут, не содержащий пустых компонент.
Монотонным блоком D-системы называется бесконфликтный блок, не содержащий D-кортежей со всеми пустыми компонентами.
Пример:
Т[XYZ] =
C =[XYZ] = [{A} * {c}]

Матричные свойства АК-объектов (продолжение)
Новые классы КНФ
Теорема 6. Если D-система Q содержит монотонный блок, то она непуста.
Пусть Q = , T11 – подматрица Q, не содержащая D-кортежей со всеми
пустыми компонентами, T21 – подматрица Q с D-кортежами, содержащими только пустые компоненты.
Теорема 7. Если в D-системе Q имеется бесконфликтный блок, то Q непуста, если и только если при разложении ее в блочную матрицу непустой является D‑система, представленная блоком T22.
Пример:
Q = =

Ортогонализация
Используется как для сокращения трудоемкости операций, так и при анализе измеримых систем (см. ниже)
В логике ортогональными называются функции вида F1 F2…  Fn,
у которых любая пара (Fi, Fj ) функций не имеет общих выполняющих подстановок.
Ортогональная С-система – это С-система, у которой пересечение любой пары
С-кортежей пусто.
Основные теоремы ортогонализации
для АК-объектов с произвольными компонентами
Пусть Q1, Q2, ..., Qm-1, Qm – произвольные множества.
Теорема 5. D-кортеж вида ]Q1 Q2 ... Qm-1 Qm[ преобразуется в эквивалентную
ортогональную C-систему .
Теорема 6. Если P и Q – ортогональные C-системы, то их пересечение либо пусто, либо состоит из одного C-кортежа, либо является ортогональной C‑системой.

Возможности распараллеливания вычислений

План доклада
1. Логический анализ: алгебраический подход и теория формальных систем (ТФС)
2. Алгебра кортежей (АК): основные определения
3. Представление в АК основных видов данных и знаний
4. Новые возможности логического анализа в АК
5 Семантический анализ информации
6. Методы снижения трудоемкости в АК
7. Метрические аспекты АК
8. Выводы

Метрические аспекты АК: квантование интервалов
Аксиомы меры μ множеств A и B:
1)μ ≥ 0;
2) (∀ A, B) μ(A ∪ B) = μ(A) + μ(B) − μ(A ∩ B).
Если атрибуты С-системы (С-кортежа) содержат интервалы числовой оси, то они разбиваются на элементарные интервалы, пересечение любой пары которых либо пусто, либо имеет единственную точку сочленения.
Кванты - точки и открытые интервалы такого разбиения. Точка определяется как вырожденный интервал с нулевой мерой. Кванты несовместны.
Пример:
E3 = {c, d, e, f, (c, d), (d, e), (e, f)}
Ei = , μ(Ei) =
Теорема 5.1. Если каждая компонента C-кортежа имеет конечную меру, то мерой C-кортежа является произведение мер его компонент.
Теорема 5.2. Мера ортогональной C-системы равна сумме мер содержащихся в ней C-кортежей.

Метрические аспекты АК: свойства АК-объектов
Для АК-объектов, погруженных в вероятностное пространство или в любое другое нормированное пространство с мерой каждого атрибута, равной 1:
мера полной компоненты (*) в C-кортежах и C-системах равна 1;
мера любого частного универсума равна 1;
мера любого АК-объекта есть число в интервале [0, 1];
мера пустого АК-объекта равна 0;
для произвольного АК-объекта A мера его дополнения равна 1 – μ(A);
для пары АК-объектов A и B
μ(A ∪G B) = μ(A) + μ(B) – μ(A ∩G B);
в любом АК-объекте после разбиения каждой компоненты на элементарные кванты мера компоненты есть сумма мер квантов, в ней содержащихся.
В двумерном пространстве:

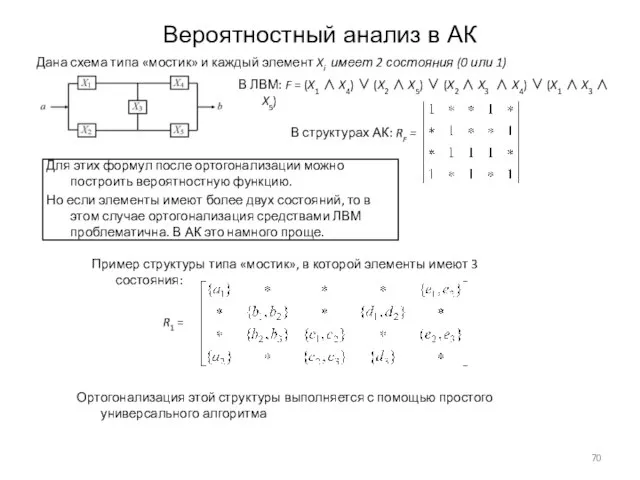
Вероятностный анализ в АК
Дана схема типа «мостик» и каждый элемент Xi имеет 2 состояния (0 или 1)
В ЛВМ: F = (X1 ∧ X4) ∨ (X2 ∧ X5) ∨ (X2 ∧ X3 ∧ X4) ∨ (X1 ∧ X3 ∧ X5)
Для этих формул после ортогонализации можно построить вероятностную функцию.
Но если элементы имеют более двух состояний, то в этом случае ортогонализация средствами ЛВМ проблематична. В АК это намного проще.
Ортогонализация этой структуры выполняется с помощью простого универсального алгоритма
R1 =
Пример структуры типа «мостик», в которой элементы имеют 3 состояния:
В структурах АК: RF =

Уравнение регрессии
Если АК-объект преобразован в ортогональную С-систему, то в вероятностном пространстве его можно представить как уравнение регрессии, в котором переменными являются вероятности элементарных событий, а значением функции – вероятность события, заданного этим АК‑объектом.
Пример 1 – система с двумя состояниями
АК-объект Уравнение регрессии
p1(1–p3)+(1–p2)p3+(1–p1)p2.
Пример 2 – система с тремя состояниями
АК-объект Уравнение регрессии
(p(a1) + p(a2))(1– p(b2))+(1– p(a1) – p(a2))(p(b1)+ p(b2)).

Вероятностная логика
В логико-вероятностных методах (ЛВМ) решается прямая задача расчета вероятности:
заданы вероятности элементарных событий в атрибутах;
необходимо вычислить вероятность события, выраженного АК-объектом (или соответствующей ему логической формулой).
В вероятностной логике решается обратная задача расчета вероятности:
заданы вероятности сложных событий;
необходимо вычислить вероятности других сложных событий.
При использовании АК в этом случае промежуточным этапом вычисления является вычисление вероятностей элементарных событий или некоторых сложных событий, которые в данной системе можно использовать в качестве атомов.

Задача 1
(Nilsson N. J. Probabilistic Logic // Artificial Intelligence, 28, 1986, pp. 71-87):
Дано: p(A) = p1 и p(A ⊃ B) = p2.
Найти: оценку p(B).
Решение в структурах АК:
Используем универсум A×B = {0, 1}2. Тогда
A = [1 *]; B = [* 1]; A ⊃ B = ∨ B = ]0 1[ = .
Получаем систему из двух уравнений
p(A) = p1;
(1 – p(A)) + p(A) p(B) = p2.
Из этой системы несложно вывести
p(B) =
У Н. Нильсона ответ p2 + p1 –1 ≤ p(B) ≤ p2.

Задача 2

Продолжение задачи 2

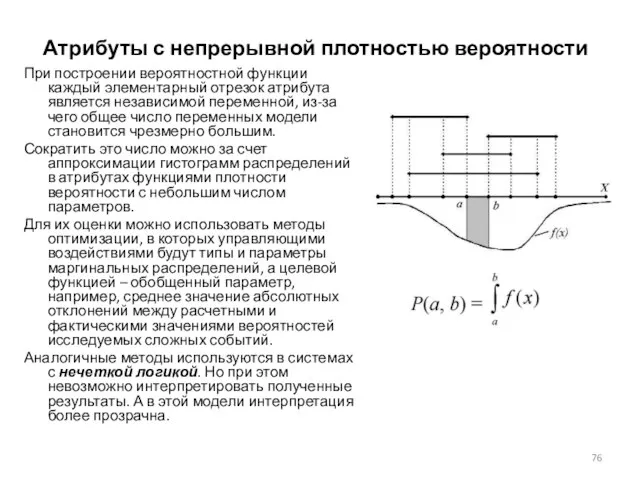
Атрибуты с непрерывной плотностью вероятности
При построении вероятностной функции каждый элементарный отрезок атрибута является независимой переменной, из-за чего общее число переменных модели становится чрезмерно большим.
Сократить это число можно за счет аппроксимации гистограмм распределений в атрибутах функциями плотности вероятности с небольшим числом параметров.
Для их оценки можно использовать методы оптимизации, в которых управляющими воздействиями будут типы и параметры маргинальных распределений, а целевой функцией – обобщенный параметр, например, среднее значение абсолютных отклонений между расчетными и фактическими значениями вероятностей исследуемых сложных событий.
Аналогичные методы используются в системах с нечеткой логикой. Но при этом невозможно интерпретировать полученные результаты. А в этой модели интерпретация более прозрачна.

Заключение
Разработанная алгебра кортежей и ее методы:
позволяют унифицированно обрабатывать данные и знания, представленные в виде совокупности многоместных отношений с различными схемами;
ускоряют выполнение процедур логического вывода за счет:
1) удобства распараллеливания вычислений,
2) использования матричных свойств отношений, а также новых структурных и статистических классов КНФ с полиномиально распознаваемым свойством выполнимости;
дают возможность по-новому организовывать процедуры логического вывода;
позволяют моделировать модифицируемые рассуждения, не нарушая законов классической логики.

Дальнейшие направления исследований
моделирование интеллектуальных динамических систем в рамках ситуационного подхода;
контекстно-ориентированные системы управления базами данных и знаний;
исследование дополнительных возможностей погружения структур АК в измеримые пространства;
моделирование пространственно-временных рассуждений.

Кулик Б.А. Система логического программирования на основе алгебры кортежей // Известия РАН. Техническая. кибернетика. 1993. № 3. С. 226-239.
Кулик Б.А. Новые классы КНФ с полиномиально распознаваемым свойством выполнимости // Автоматика и телемеханика. 1995. № 2. С. 111-124.
Кулик Б.А. Представление логических систем в вероятностном пространстве на основе алгебры кортежей. 1. Основы алгебры кортежей //Автоматика и телемеханика. 1997. № 1. С. 126–136.
Кулик Б.А., Наумов М. В. Представление логических систем в вероятностном пространстве на основе алгебры кортежей. 2. Измеримые логические системы // Автоматика и телемеханика. 1997. № 2. С. 169–179.
Фридман А.Я. Ситуационный подход к моделированию промышленно-природных комплексов и управлению их структурой. Труды IV международной конференции "Идентификация систем и задачи управления". Москва, 25-28 января 2005 г. ИПУ РАН, 2005 г. - С.1075-1108.
Зуенко А.А., Фридман А.Я. Логический вывод при семантическом анализе нерегламентированных путевых запросов. // Одиннадцатая национальная конференция по искусственному интеллекту с международным участием КИИ-2008 (28 сентября - 3 октября 2008 г., Дубна, Россия): Труды конференции. Т.1. – М.: ЛЕНАНД, 2008. – С.298-304.
Зуенко А.А., Фридман А.Я. Контекстный подход в системах сопровождения открытых моделей предметной области // Искусственный интеллект и принятие решений. 2008. №3. С.41-51.
Зуенко А.А., Фридман А.Я. Развитие алгебры кортежей для логического анализа баз данных с использованием двуместных предикатов // Известия РАН. Теория и системы управления. 2009. №2. – С.95-103.
Зуенко А.А., Кулик Б.А., Фридман А.Я. Анализ корректности запросов к базам данных систем концептуального моделирования средствами алгебры кортежей / Искусственный интеллект. Интеллектуальные системы (ИИ-2009) // Материалы Х Международной научно-технической конференции. - Таганрог: Изд-во ТТИ ЮФУ, 2009. - С.86-88.
Список литературы