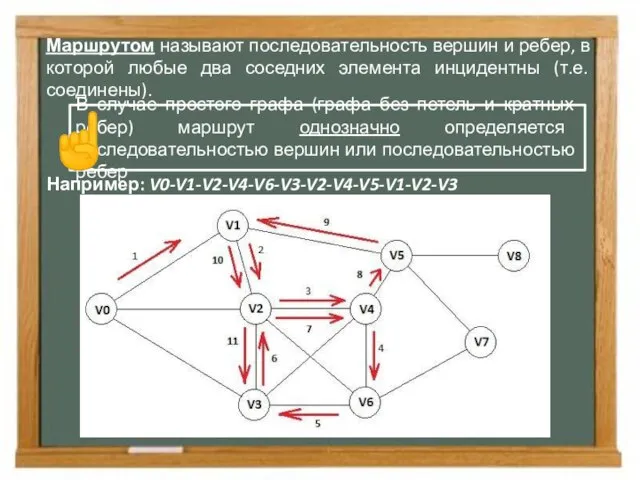
Маршрут, цепь, цикл Маршрутом называют последовательность вершин и ребер, в которой любые два соседних элемента инцидентны (т.е. со

Маршрут, цепь, цикл

Маршрутом называют последовательность вершин и ребер, в которой любые два соседних элемента инцидентны (т.е. соединены).
Например: V0-V1-V2-V4-V6-V3-V2-V4-V5-V1-V2-V3
В случае простого графа (графа без петель и кратных ребер) маршрут однозначно определяется последовательностью вершин или последовательностью ребер
☝

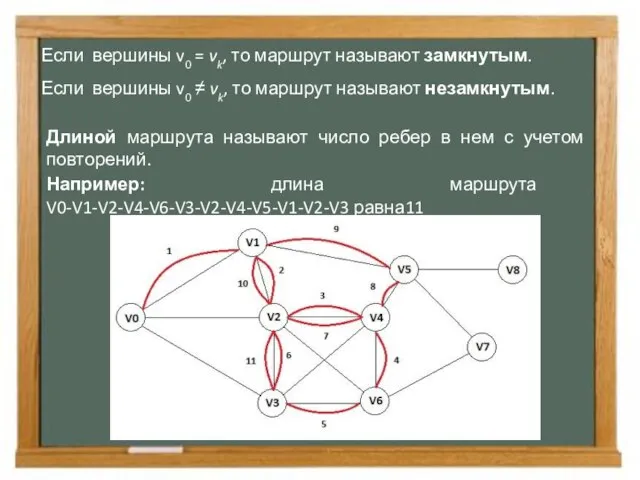
Если вершины v0 = vk, то маршрут называют замкнутым.
Если вершины v0 ≠ vk, то маршрут называют незамкнутым.
Длиной маршрута называют число ребер в нем с учетом повторений.
Например: длина маршрута V0-V1-V2-V4-V6-V3-V2-V4-V5-V1-V2-V3 равна11

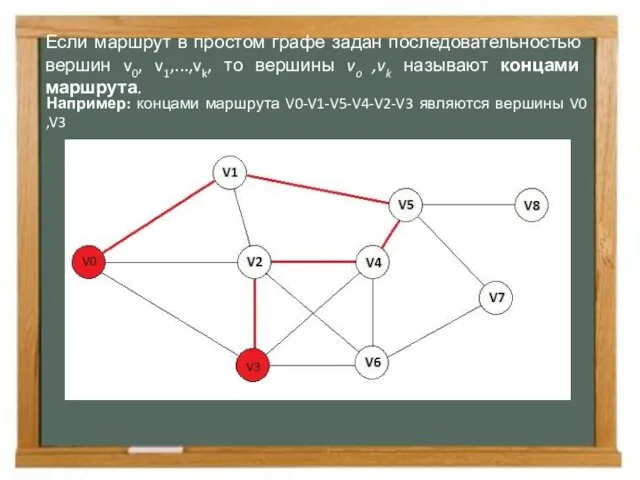
Если маршрут в простом графе задан последовательностью вершин v0, v1,...,vk, то вершины vo ,vk называют концами маршрута.
Например: концами маршрута V0-V1-V5-V4-V2-V3 являются вершины V0 ,V3

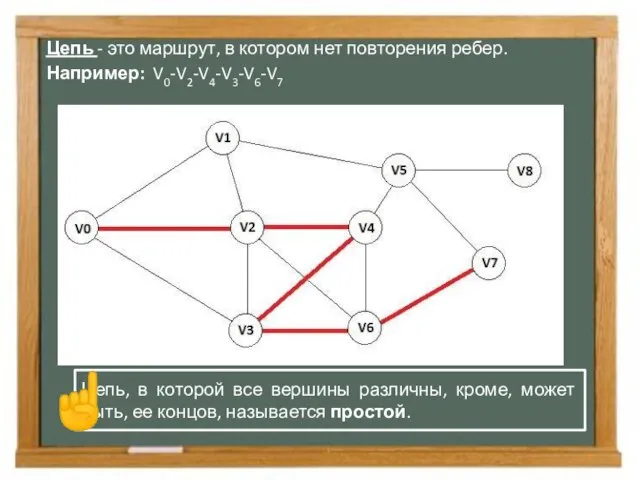
Цепь - это маршрут, в котором нет повторения ребер.
Например: V0-V2-V4-V3-V6-V7
Цепь, в которой все вершины различны, кроме, может быть, ее концов, называется простой.
☝

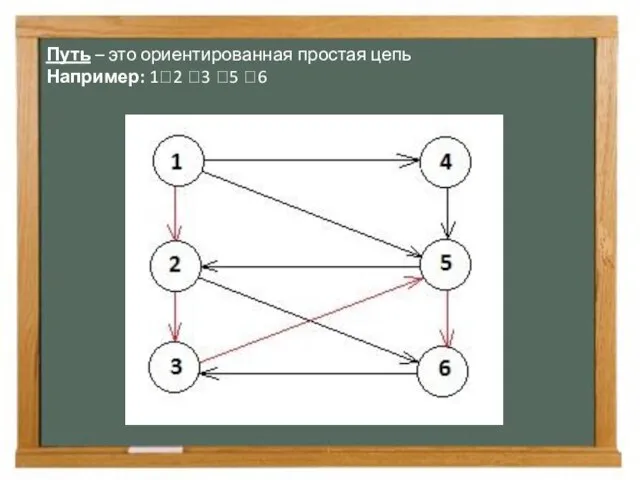
Путь – это ориентированная простая цепь
Например: 1⭢2 ⭢3 ⭢5 ⭢6

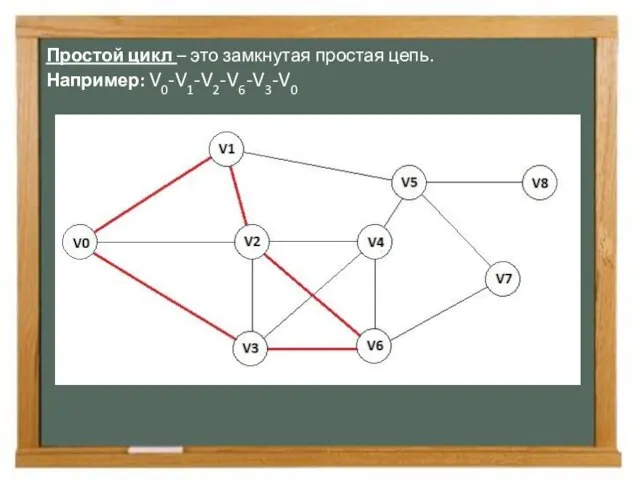
Простой цикл – это замкнутая простая цепь.
Например: V0-V1-V2-V6-V3-V0

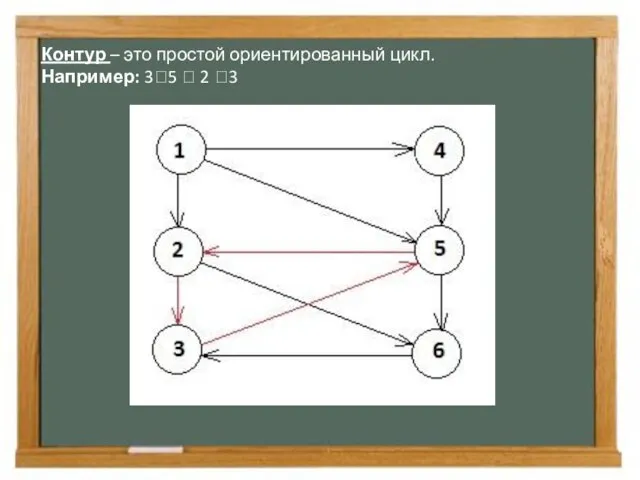
Контур – это простой ориентированный цикл.
Например: 3⭢5 ⭢ 2 ⭢3

Леонард Эйлер
(1707 —1783)
Эйлеров путь (эйлерова цепь) — это путь, проходящий по всем ребрам графа и притом только по одному разу.
Эйлеров цикл — это эйлеров путь, являющийся циклом.

Расстояние между вершинами, диаметр, мост

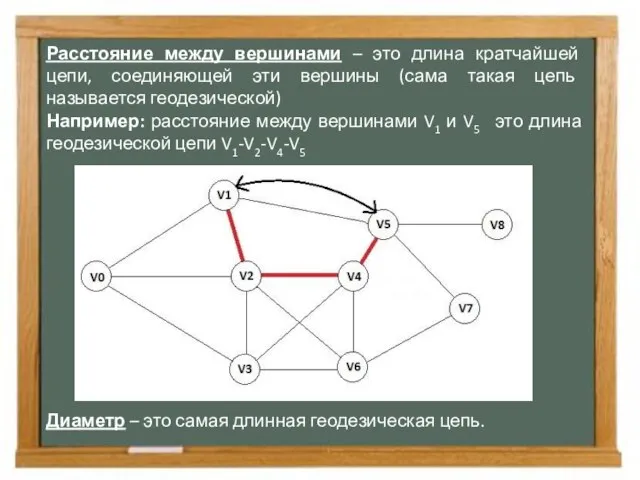
Расстояние между вершинами – это длина кратчайшей цепи, соединяющей эти вершины (сама такая цепь называется геодезической)
Например: расстояние между вершинами V1 и V5 это длина геодезической цепи V1-V2-V4-V5
Диаметр – это самая длинная геодезическая цепь.

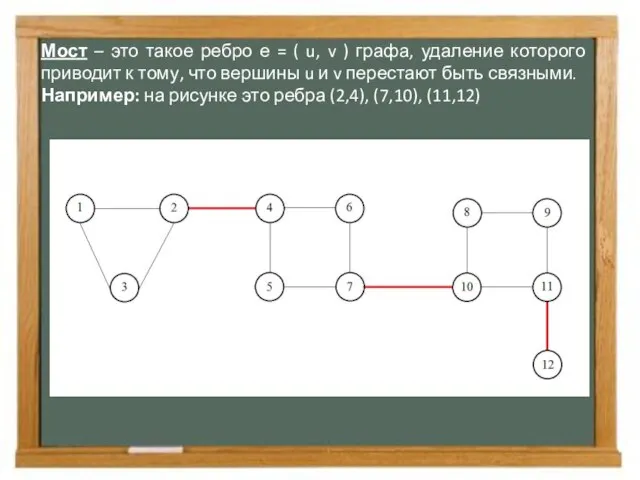
Мост – это такое ребро е = ( u, v ) графа, удаление которого приводит к тому, что вершины u и v перестают быть связными.
Например: на рисунке это ребра (2,4), (7,10), (11,12)

Точка сочленения, блок

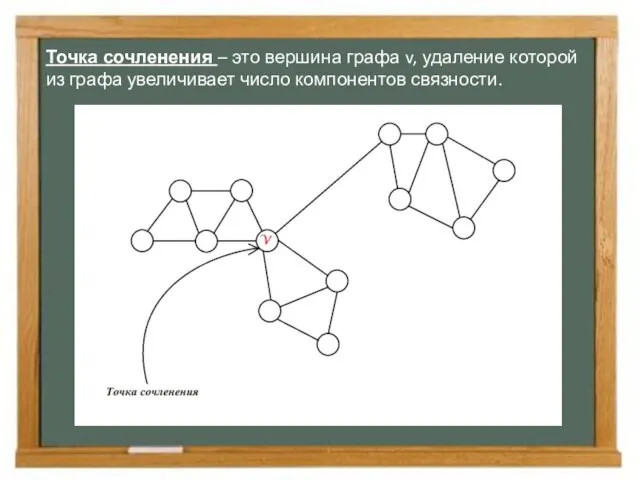
Точка сочленения – это вершина графа v, удаление которой из графа увеличивает число компонентов связности.

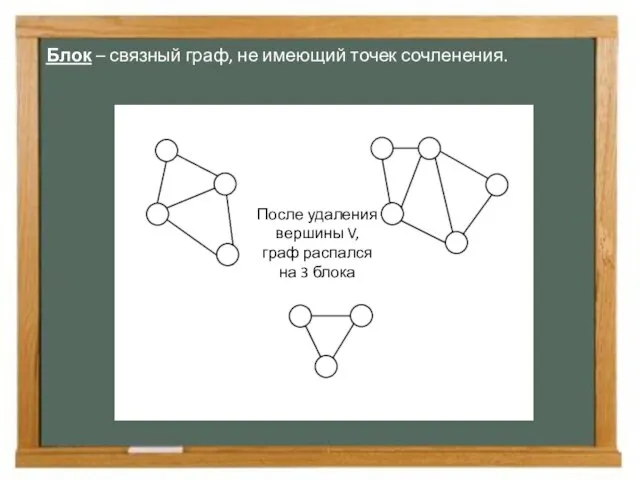
Блок – связный граф, не имеющий точек сочленения.
После удаления вершины V, граф распался на 3 блока

Спасибо за внимание!