Методы решения задач на нахождение наибольшего и наименьшего значения величин. (задания для учащихся 8-9 классов, углубленное изуч

Алгоритм изучения темы
Знакомство с понятиями прикладных задач математики.
Схема решения оптимизационных задач.
Теоремы, применяемые при решении таких задач.
Методы решения оптимизационных задач:
применение некоторых теорем;
использование свойств квадратного трехчлена;
применение неравенства Коши.

Знакомство с понятиями прикладных задач математики.
Задачи на нахождение наибольшего и наименьшего значений какой-либо величины, часто применяемые в практической деятельности, называются оптимизационными. Для правильного решения таких задач необходимо выполнить их переформулировку, стремясь формализировать условия, первоначально заданные в описательной форме.

Схема решения оптимизационных задач
Проанализировав условие задачи, определить, наибольшее или наименьшее значение какой величины требуется найти (т.е. какую величину нужно оптимизировать).
Принять за независимую переменную одну из неизвестных величин и обозначить её буквой x. Определить её границы изменения.
Задать функцию y=f(x).
Найти средствами математики наибольшее или наименьшее значение на промежутке изменения х.
Интерпретировать результат для рассматриваемой задачи.

Пример решения оптимизационных задач.

Теоремы и следствия из них для решения оптимизационных задач .

Доказательство теорем

Решение оптимизационных задач с применением доказанных теорем

Задача №2. Даны две параллельные прямые и точка А между ними, служащая вершиной прямого угла прямоугольного треугольника, у которого две другие вершины лежат на каждой из прямых. Какое положение должен занимать треугольник, чтобы его площадь была наибольшей?
А
Е
С
В
Д

Теорема об использовании свойств квадратного трехчлена

Решение задач с использованием свойств квадратного трехчлена

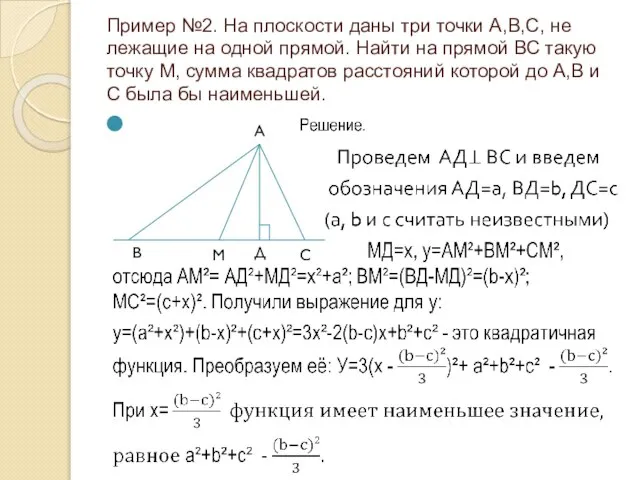
Пример №2. На плоскости даны три точки А,В,С, не лежащие на одной прямой. Найти на прямой ВС такую точку М, сумма квадратов расстояний которой до А,В и С была бы наименьшей.
А
В
С
Д
М

Классическое неравенство Коши

Применение неравенства Коши

Решить самостоятельно.