Слайд 2Введение
Содержание работы - задача k коммивояжёров.
Цель - минимизация стоимости объезда городов

k коммивояжёрами.
На практике постановка задачи k коммивояжёров имеет множество вариантов.
В данной работе сформулирована упрощенная постановка задачи без учета максимальной загрузки одного коммивояжёра, задержки при посещении каждого города, возможности существования нескольких баз и т. д.
Слайд 3Формальная постановка задачи
Среди городов вводится база - город, где начинаются и заканчиваются

все пути коммивояжёров. Стоимость переезда из города i в город j будет задаваться матрицей, где нужное значение будет храниться на пересечении i-той строки и j-того столбца. Определим задачу так:
1. На вход алгоритма поступает матрица расстояний между n городами и множество значений расстояний от каждого города до базы.
2. Необходимо найти k замкнутых маршрутов, где k > 1, со следующими свойствами:
2.1. Через каждый город должен проходить один и только один маршрут, причём только один раз;
2.2. Все маршруты должны проходить через базу;
2.3. Для любой пары полученных маршрутов количество городов в них не должно отличаться больше чем на единицу.
3. Суммарная длина полученных маршрутов должна быть как можно меньше.
Слайд 4Рассматриваемые алгоритмы
Оптимальное разрезание общего маршрута по всем городам
Предварительное разделение на группы для

каждого коммивояжёра
Последовательное деление на 2 группы
Добавление городов на основе минимума расстояний
Добавление городов на основе разности расстояний
Последовательное деление на 3 группы
Обменная оптимизация
Для всех городов
Для ограниченного множества городов
Слайд 5Угловая сортировка городов на плоскости
Является исключением среди рассматриваемых методов, поскольку не удовлетворяет

формальной постановке задачи.
Использует информацию об углах между городами, если они расположены на плоскости.
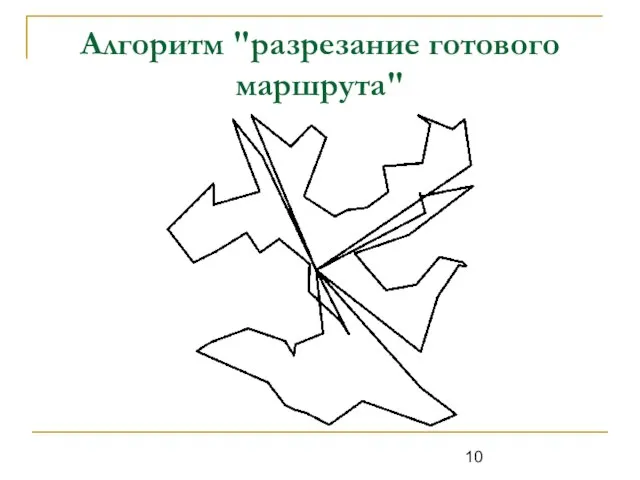
Слайд 6Алгоритм разрезания "общего " маршрута
1. Решить задачу коммивояжёра
2. Найти количество городов

для каждого коммивояжёра
3. В предварительно построенном маршруте выбрать некоторый город в качестве начального.
4. Городами для объезда 1-вым коммивояжёром будут первые N[1] городов, начиная с выбранного начального. Последующий отрезок маршрута из N[2] городов будет участком для 2-го коммивояжёра и т. д. В результате этого этапа мы получим k незамкнутых последовательностей нужной длины.
5. К каждой такой последовательности добавим базу и замкнём её.
6. Запомним полученную длину всех маршрутов и повторим операцию с шага 4, но начальный город сместим на один относительно предыдущего.
7. Шаг 6 будем повторять Nmin раз, где Nmin - это число на один меньше, чем длина самого короткого пути среди коммивояжёров, полученных на шаге 2.
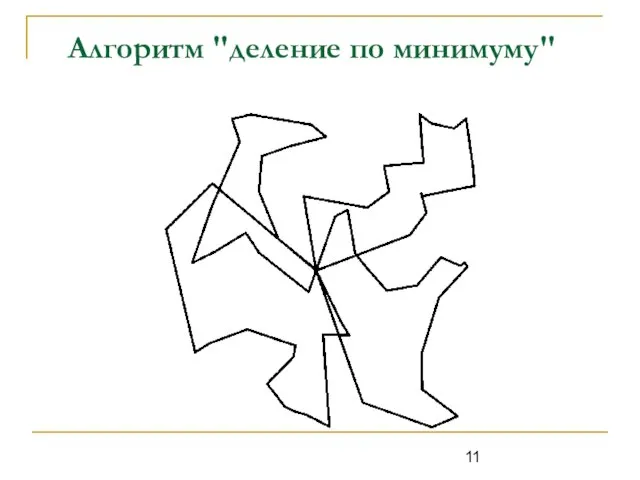
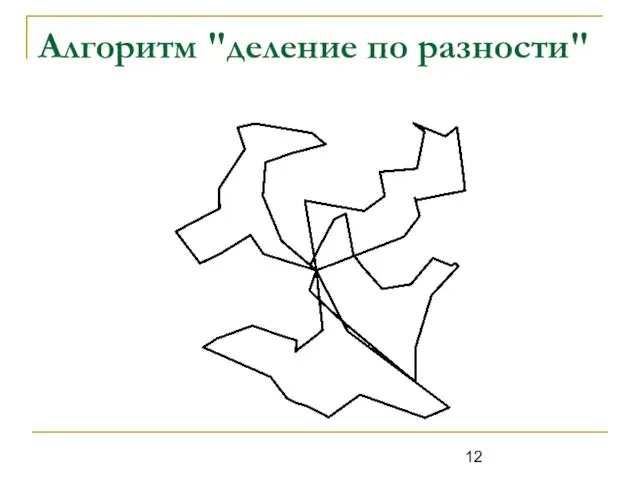
Слайд 7Метод предварительного разделения городов на группы для каждого коммивояжёра
Наиболее эффективным является последовательное

разделение на 2 группы. Рассмотрены 2 метода выбора нового города для добавления:
На основе минимума расстояний.
На основе разности расстояний. Качество работы выше.
Слайд 8Обменная оптимизация
После очередного разделения городов на 2 группы:
1. Рассмотрим все возможные пары

городов, где первый город будет принадлежать первой, а второй - второй группе;
2. Для каждой такой пары выполним пробный обмен городами. То есть первый город попадёт во вторую группу, а второй - в первую.
3. Выполнив обмен, подсчитаем сумму длин рёбер минимального остова в каждой группе, прибавив длину самого длинного ребра в нём.
4. Найдём оценку из шага 3 для всех возможных пар. Если минимальное значение таких оценок меньше, чем в исходных группах, то совершим обмен.
Оптимизация проводится для всех городов в группах
Оптимизация проводится для ограниченного множества городов
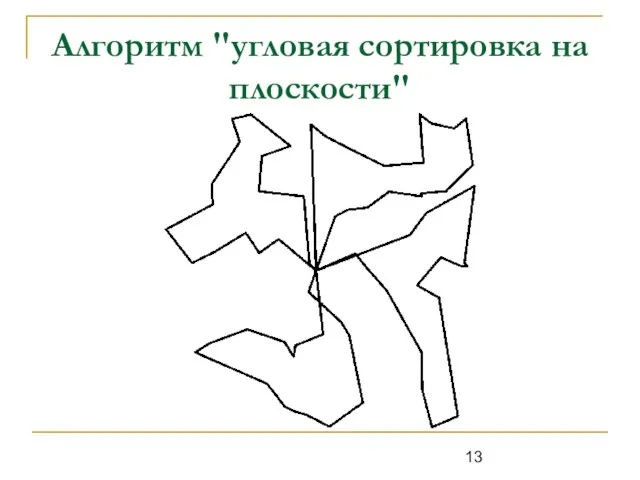
Слайд 9Угловая сортировка городов на плоскости
1. Для каждого города вычисляются углы между ними

и осью X.
2. Множество городов сортируются по возрастанию углов.
3. Вычисляется количество городов для каждой будущей группы. По результатам вычислений получаем массив Ni.
4. Первые N1 городов из отсортированного списка отнесём к первой группе, последующие N2 городов - ко второй и. т. д., к каждой группе добавим по базе.
5. Для каждой полученной группы вычисляется минимальная оценка возможного решения.
6. Повторяем действия на шаге 4, но при построении отступаем на один город и находим оценку, описанную на шаге 5.
7. Выбирается то разбиение, где оценка минимальна и выполняется поиск окончательных маршрутов решением простой ЗК внутри каждой группы.
Слайд 10Алгоритм "разрезание готового маршрута"
Слайд 13Алгоритм "угловая сортировка на плоскости"
Слайд 14Вычислительный эксперимент
При тестировании описанных методов выполнялся многократный их запуск на случайно

сгенерированном множестве городов. При генерации города располагались на плоскости равномерно в единичном квадрате с независимыми координатами. Результаты приведены в отношении к нижней оценке точного решения задачи коммивояжёра.
Обменная оптимизация проводилась только в частичном варианте, поскольку многократное нахождение минимального остова занимает слишком много времени.
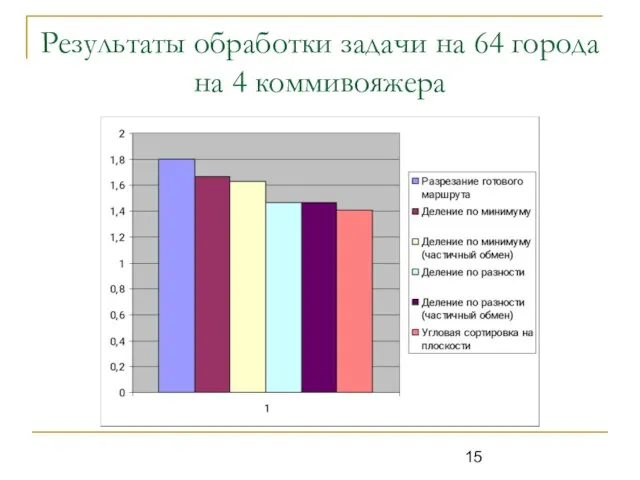
Слайд 15Результаты обработки задачи на 64 города на 4 коммивояжера
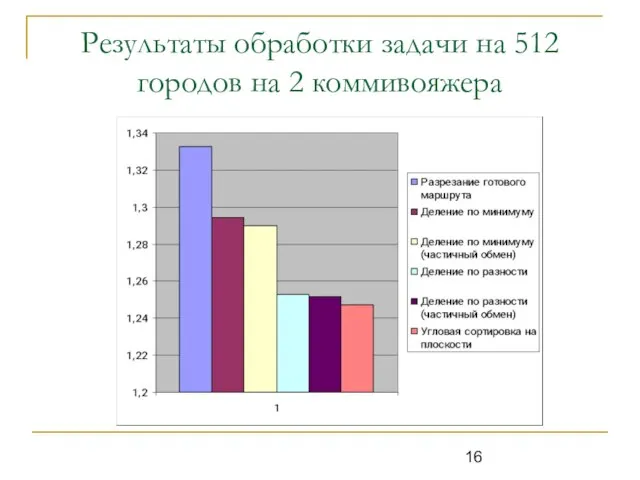
Слайд 16Результаты обработки задачи на 512 городов на 2 коммивояжера
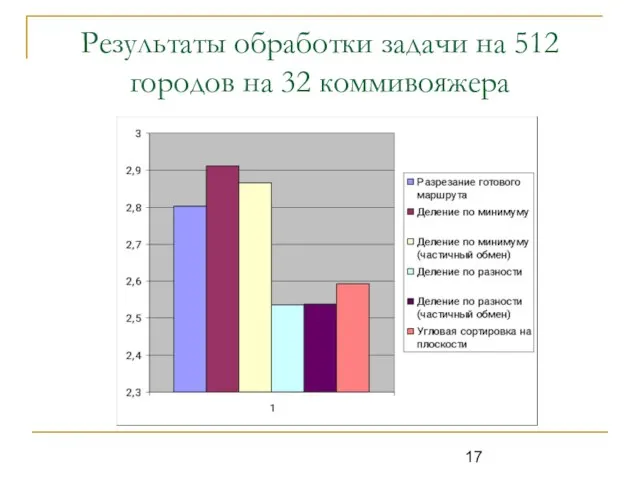
Слайд 17Результаты обработки задачи на 512 городов на 32 коммивояжера
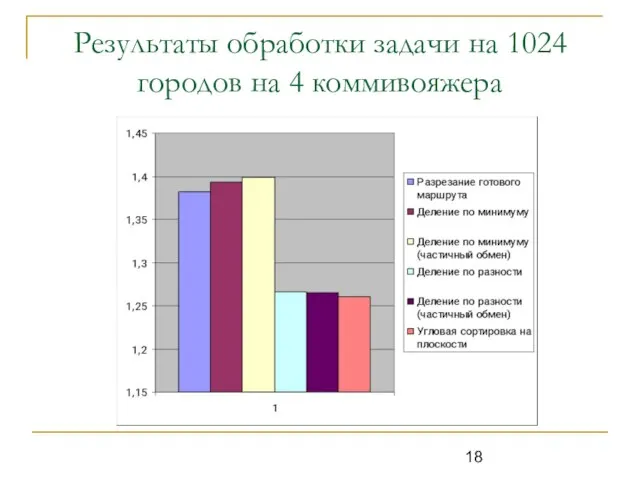
Слайд 18Результаты обработки задачи на 1024 городов на 4 коммивояжера
Слайд 19Заключение
Сформулирована сбалансированная задача k коммивояжеров
Предложены некоторые методы приближенного её решения
Поставлен вычислительный эксперимент

для сравнения качества работы предложенных алгоритмов и выполнен статистический анализ ранговым критерием Уилкоксона
Подготовлена программная библиотека
















 техника безоп
техника безоп шиповое соединение
шиповое соединение Взаємодія України та Португалії
Взаємодія України та Португалії Основы конституционного строя России
Основы конституционного строя России Обсуждение художественного фильма Полосатый рейс с точки зрения трудового права
Обсуждение художественного фильма Полосатый рейс с точки зрения трудового права Планирование веб-релизовв условиях многопоточности задачсо скачущими приоритетами
Планирование веб-релизовв условиях многопоточности задачсо скачущими приоритетами Способы кодирования информации.
Способы кодирования информации. Технология в жизни человека и общества
Технология в жизни человека и общества Пикапы маслозаправщики. Схема движения по маршрутам
Пикапы маслозаправщики. Схема движения по маршрутам «Магнетизм и его изучение». Учитель физики Балашова Н. А. Троицк 2011г.
«Магнетизм и его изучение». Учитель физики Балашова Н. А. Троицк 2011г.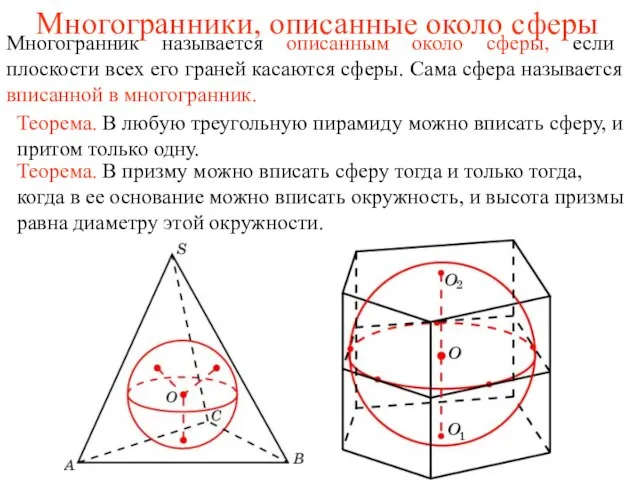 Многогранники, описанные около сферы
Многогранники, описанные около сферы Юношеский возраст. Лекция 8.2
Юношеский возраст. Лекция 8.2 Охрана земельных ресурсов – залог эффективного ведения сельского хозяйства
Охрана земельных ресурсов – залог эффективного ведения сельского хозяйства Элементы суггестивного управления в системе педагогической деятельности учителя
Элементы суггестивного управления в системе педагогической деятельности учителя Рязанские народные ремесла и промыслы
Рязанские народные ремесла и промыслы The best job in the world
The best job in the world  ИНФЕКЦИОННЫЙ КОНТРОЛЬ ИНФЕКЦИОННАЯ БЕЗОПАСНОСТЬ
ИНФЕКЦИОННЫЙ КОНТРОЛЬ ИНФЕКЦИОННАЯ БЕЗОПАСНОСТЬ Рекламное агентство
Рекламное агентство 1С-Битрикс: Сайт школы
1С-Битрикс: Сайт школы Презентация Microsoft Office PowerPoint
Презентация Microsoft Office PowerPoint Работа выполнена в рамках проекта «Повышения квалификаций различных категорий работников образования и формирование у них базов
Работа выполнена в рамках проекта «Повышения квалификаций различных категорий работников образования и формирование у них базов FN1_LessonOne
FN1_LessonOne Modal verb May/might
Modal verb May/might Образ ребенка в киноискусстве XX
Образ ребенка в киноискусстве XX Потребление воды и минеральных ресурсов
Потребление воды и минеральных ресурсов Эвдемонизм - это гуманизм
Эвдемонизм - это гуманизм 07_0___163
07_0___163 Презентация "Орфей и Эвридика" - скачать презентации по МХК
Презентация "Орфей и Эвридика" - скачать презентации по МХК