Позиционные и непозиционные системы счисления Одно и то же число можно представить по-разному. Например, число четыре можно предс

Представление целых неотрицательных чисел
В позиционных системах значение записи целого числа определяется по следующему правилу: пусть anan-1an-2…a1a0 — запись числа A, аi – цифры, тогда
A = an·pn+an-1·pn-1 +an-2·pn-2+...+a1·p1+ a0·p0 (1),
где p — целое число большее 1, которое называется основанием системы счисления .
Для того, чтобы при заданном p любое неотрицательное целое число можно было бы записать по формуле (1) и притом единственным образом, числовые значения различных цифр должны быть различными целыми числами, принадлежащими отрезку от 0 до p-1.
Пример: 1) Десятичная система p = 10
цифры: 0,1,2,3,4,5,6,7,8,9
число 3635 = 3·103+6·102+3·101+5·100
2) Троичная система p = 3
цифры: 0,1,2
число 1213 = 1·32+2·31+1·30
Замечание: нижним индексом в записи числа обозначается основание системы счисления, в которой записано число. Для десятичной системы счисления индекс можно не писать.

Представление отрицательных и дробных чисел
Во всех позиционных системах для записи отрицательных чисел так же как и в десятичной системе используется знак ‘–‘.
Для отделения целой части числа от дробной используется запятая.
Значение записи anan–1an–2…a1a0, a–1a–2…am–2am–1am числа A определяется по формуле, являющейся обобщением формулы (1):
A = an·pn+an–1·pn–1+an–2·pn–2+…+a1·p1+a0·p0+a–1·p–1+a–2·p–2+…+am–2·p–(m–2)+am–1·p–(m–1)+amp–m (2),
Пример:
36,6 = 3·101+6·100+6·10–1
–3,2145 = –(3·50+2·5–1+1·5–2+4·5–3)

Перевод чисел из произвольной системы счисления в десятичную
Следует понимать, что при переводе числа из одной системы счисления в другую количественное значение числа не изменяется, а меняется только форма записи числа, так же как при переводе названия числа, например, с русского языка на английский.
Перевод чисел из произвольной системы счисления в десятичную выполняется непосредственным вычислением по формуле (1) для целых и формуле (2) для дробных чисел.
Перевод чисел из десятичной системы счисления в произвольную
Перевести число из десятичной системы в систему с основанием p – значит найти коэффициенты в формуле (2). Иногда это легко сделать простым подбором.
Например, пусть нужно перевести число 23,5 в восьмеричную систему. Нетрудно заметить, что
23,5 = 16+7+0,5 = 2·8+7+4/8 = 2·81+7·80+4·8–1 =27,48.
Понятно, что не всегда ответ столь очевиден.
В общем случае применяется способ перевода отдельно целой и дробной частей числа.

Для перевода целых чисел применяется следующий алгоритм (полученный на основании формулы (1)):
1. Найдем частное и остаток от деления числа на p. Остаток будет очередной цифрой ai (j=0,1,2 …) записи числа в новой системе счисления.
2. Если частное равно нулю, то перевод числа закончен, иначе применяем к частному пункт 1.
Замечание 1. Цифры ai в записи числа нумеруются справа налево.
Замечание 2. Если p>10, то необходимо ввести обозначения для цифр с числовыми значениями, большими или равными 10.
Пример:
Перевести число 165 в семеричную систему счисления.
165:7 = 23 (остаток 4) => a0 = 4
23:7 = 3 (остаток 2) => a1 = 2
3:7 = 0 (остаток 3) => a2 = 3
Выпишем результат: a2a1a0, т.е. 3247.
Выполнив проверку по формуле (1), убедимся в правильности перевода:
3247=3·72+2·71+4·70=3·49+2·7+4 = 147+14+4 = 165.

Для перевода дробных частей чисел применяется алгоритм, полученный на основании формулы (2):
1. Умножим дробную часть числа на p.
2. Целая часть результата будет очередной цифрой am (m = –1,–2, –3 …) записи числа в новой системе счисления. Если дробная часть результата равна нулю, то перевод числа закончен, иначе применяем к ней пункт 1.
Замечание 1. Цифры am в записи числа располагаются слева направо в порядке возрастания абсолютного значения m.
Замечание 2. Обычно количество дробных разрядов в новой записи числа ограничивается заранее. Это позволяет выполнить приближенный перевод с заданной точностью. В случае бесконечных дробей такое ограничение обеспечивает конечность алгоритма.
Пример 1:
Перевести число 0,625 в двоичную систему счисления.
0,625·2 = 1,25 (целая часть 1) => a–1 =1
0,25·2 = 0,5 (целая часть 0) => a–2 = 0
0,5·2 = 1,00 (целая часть 1) => a–3 = 1
Итак, 0,62510 = 0,1012
Выполнив проверку по формуле (2), убедимся в правильности перевода:
0,1012=1·2–1+0·2–2+1·2–3=1/2+1/8 = 0,5+0,125 = 0,625.

Пример 2:
Перевести число 0,165 в четверичную систему счисления, ограничившись четырьмя четверичными разрядами.
0,165·4 = 0,66 (целая часть 0) => a–1=0
0,66·4 = 2,64 (целая часть 2) => a–2= 2
0,64·4 = 2,56 (целая часть 2) => a–3= 2
0,56·4 = 2,24 (целая часть 2) => a–4= 2
Итак, 0,16510 » 0,02224
Выполним обратный перевод, чтобы убедиться, что абсолютная погрешность не превышает 4–4:
0,02224 = 0·4–1+2·4–2+2·4–3+2·4–4 = 2/16+2/64+2/256 = 1/8+1/32+1/128 = 21/128 = 0,1640625
|0,1640625–0,165| = 0,00094 < 4–4 = 0,00390625

Перевод чисел в систему счисления с кратным основанием
Пусть p и q – основания двух систем счисления.
Будем называть эти системы системами счисления с кратными основаниями, если p = qn или q = pn, где n – натуральное число.
(Так, например, системы счисления с основаниями 2 и 8 являются системами счисления с кратными основаниями.)
Пусть p = qn и требуется перевести число из системы счисления с основанием q в систему счисления с основанием p.
Разобьем целую и дробную части записи числа на группы по n последовательно записанных цифр влево и вправо от запятой. Если количество цифр в записи целой части числа не кратно n, то надо дописать слева соответствующее количество нулей. Если количество цифр в записи дробной части числа не кратно n, то нули дописываются справа.
Каждая такая группа цифр числа в старой системе счисления будет соответствовать одной цифре числа в новой системе счисления.
Пример:
Переведем 1100001,1112 в четверичную систему счисления.
Дописав нули и выделив пары цифр, получим 01100001,11102.

Теперь выполним перевод отдельно каждой пары цифр, пользуясь пунктом «Перевод чисел из одной произвольной системы в другую»:
012=110=14
102=210=24
002=010=04
012=110=14
112=310=34
102=210=24
Итак, 1100001,1112 = 01100001,11102 = 1201,324.
Пусть теперь требуется выполнить перевод из системы с большим основанием q, в систему с меньшим основанием p, т.е.
q = pn.
В этом случае одной цифре числа в старой системе счисления соответствует n цифр числа в новой системе счисления.
Пример: Выполним проверку предыдущего перевода числа:
1201,324 = 1100001,11102=1100001,1112
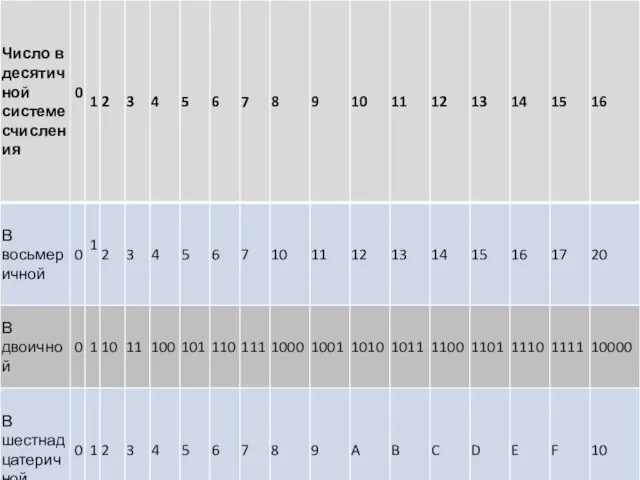
В таблице приведены значения цифр в наиболее часто используемых системах счисления.

Двоичная, восьмеричная, и шестнадцатеричная системы счисления.
В какой системе счисления лучше записывать числа – это вопрос удобства и традиций. С технической точки зрения, в ЭВМ удобно использовать двоичную систему, так как в ней для записи числа используются только две цифры 0 и 1, которые можно представить двумя легко различимыми состояниями “нет сигнала ” и “есть сигнал”.
Человеку, напротив, неудобно иметь дело с двоичными записями чисел из-за того, что они более длинные, чем десятичные и в них много повторяющихся цифр.
Поэтому, при необходимости работать с машинными представлениями чисел используют восьмеричную или шестнадцатеричную системы счисления. Основания этих систем – целые степени двойки, и поэтому числа легко переводятся из этих систем в двоичную и обратно.
В шестнадцатеричной системе есть цифры с числовыми значениями 10,11,12, 13,14,15. Для их обозначения используют первые шесть букв латинского алфавита.
Приведем таблицу чисел от 0 до 16, записанных в системах счисления с основаниями 10, 2, 8 и 16.