Описание областей влияния базисных вейвлет-функций при помощи ИТ и построение решения задачи Дирихле для некоторых специальных о
Содержание
- 2. Содержание работы. Цель работы. Основные определения. Задача Дирихле и ее решение. Основные результаты. Список литературы.
- 3. Цель работы: решение задачи Дирихле для области ограниченной концентрическими окружностями в терминах вейвлет-анализа. Решение поставленной задачи
- 4. Основные определения. Определение. Если удовлетворяет условию «допустимости»: то называется «базисным вейвлетом». Относительно каждого базисного вейвлета интегральное
- 5. Определение. Тождественно не равная нулю функция называется функцией-окном, если так же принадлежит . Центр и радиус
- 6. Представление решения задачи Дирихле для концентрического кольца Задача Дирихле. Решение где функции выражаются через элементы базиса
- 7. Основные результаты. Начнем исследование с вычисления координат центра области влияния слагаемых входящих в базисную функцию. ,
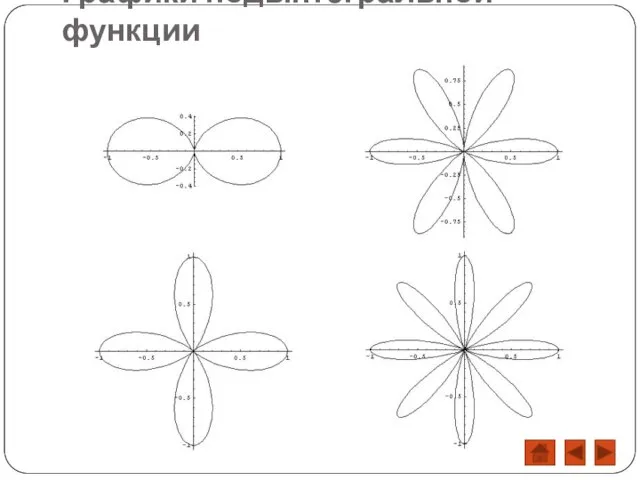
- 8. Графики подынтегральной функции
- 9. Переходим к интегрированию по круговому сектору, градусная мера, которого равна . т.е. -ое слагаемое n-ой базисной
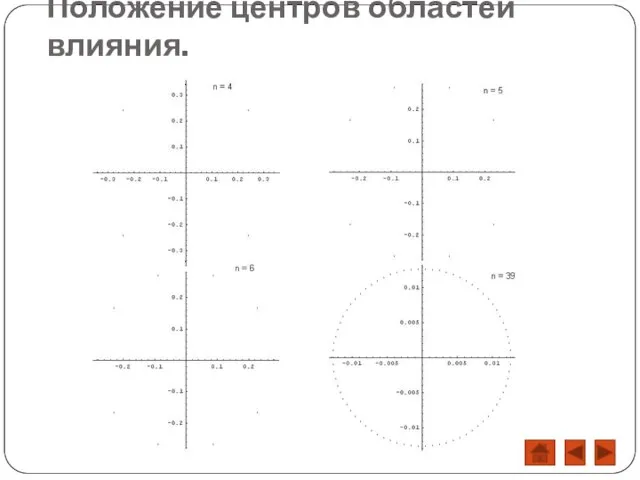
- 10. Положение центров областей влияния.
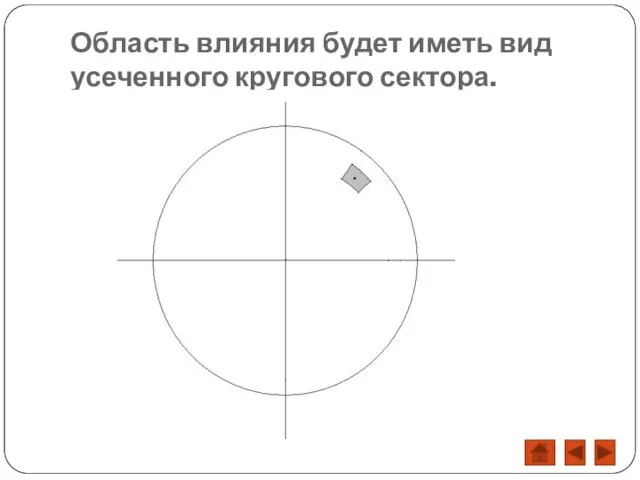
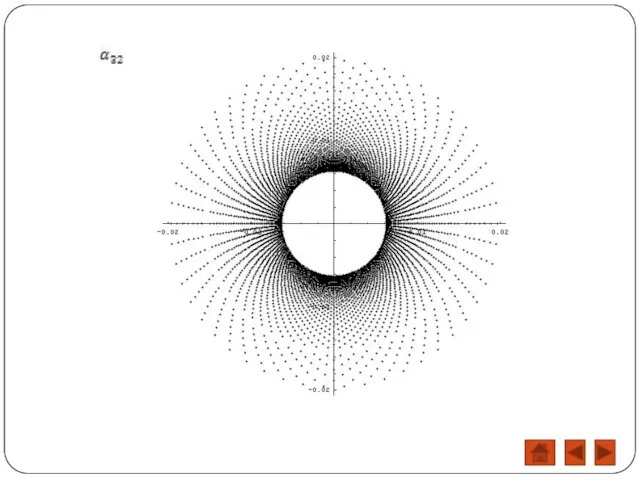
- 11. Область влияния будет иметь вид усеченного кругового сектора.
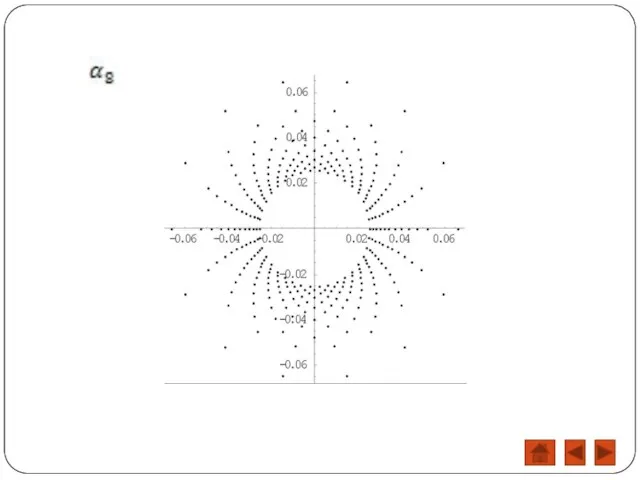
- 12. Область влияния базисных функций с различными номерами.
- 15. Радиус внутренней окружности кольца фиксирован, а т.к. область влияния базисных функций сужается и стремится к нулю,
- 16. Список литературы. Чуи К. Введение в вейвлеты. Москва: «Мир», 2001. – 412 с. Фрейзер М. Введение
- 18. Скачать презентацию










 Компьютерная зависимость
Компьютерная зависимость Форум сельской молодежи Центрального Федерального округа
Форум сельской молодежи Центрального Федерального округа Участникам ЕГЭ-2011
Участникам ЕГЭ-2011 Техника безопасности и форма одежды на уроках лыжной подготовки в школе
Техника безопасности и форма одежды на уроках лыжной подготовки в школе Наблюдения за погодой природные явления Сила и направление ветра Урок-обобщение
Наблюдения за погодой природные явления Сила и направление ветра Урок-обобщение Гражданская война И Иностранная интервенция
Гражданская война И Иностранная интервенция Save the Earth
Save the Earth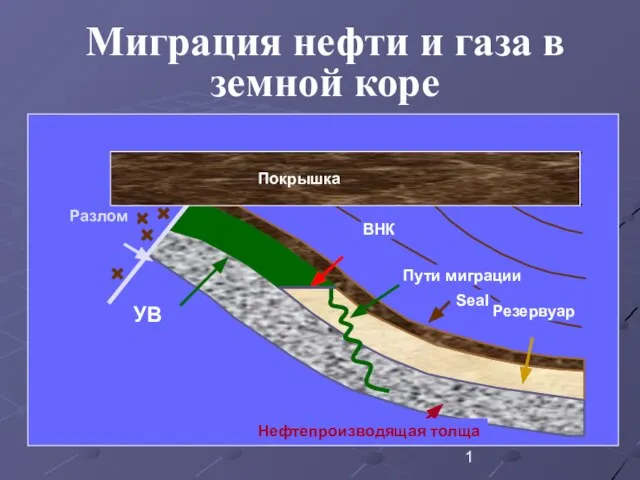 Миграция нефти и газа в земной коре
Миграция нефти и газа в земной коре 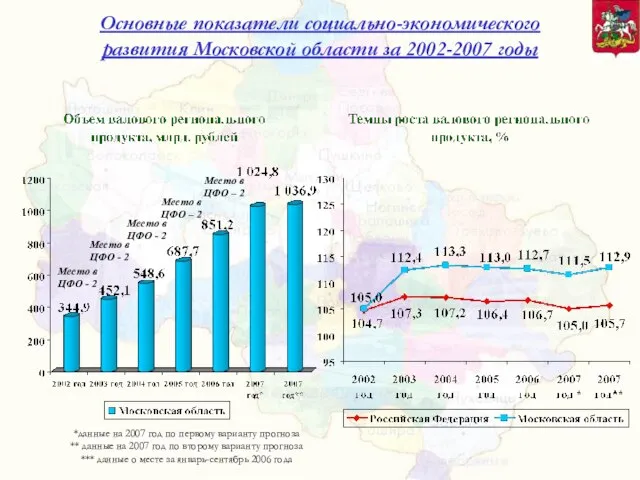 Основные показатели социально-экономического развития Московской области за 2002-2007 годы
Основные показатели социально-экономического развития Московской области за 2002-2007 годы Пирамида планирования в Казначействе России
Пирамида планирования в Казначействе России Исследовательская работа по теме:Экологические проблемы олимпиады в Сочи и пути их решения
Исследовательская работа по теме:Экологические проблемы олимпиады в Сочи и пути их решения «Заглядинская средняя общеобразовательная школа»
«Заглядинская средняя общеобразовательная школа» Классический дарвинизм
Классический дарвинизм Социологические исследования как источник информированного принятия решения в области реализации прав ребенка
Социологические исследования как источник информированного принятия решения в области реализации прав ребенка DTX Series CableAnalyzer™
DTX Series CableAnalyzer™ « Сколько весит здоровье ученика?» Составили: ученики 3-б класса Руководитель: Просвирнина Н.П учитель начальных классов МОУ-СОШ№2
« Сколько весит здоровье ученика?» Составили: ученики 3-б класса Руководитель: Просвирнина Н.П учитель начальных классов МОУ-СОШ№2 Презентация на тему Рождество обычаи и традиции
Презентация на тему Рождество обычаи и традиции Спортивно-оздоровительный клуб Аздобромир Пермь
Спортивно-оздоровительный клуб Аздобромир Пермь Market Equilibrium
Market Equilibrium Презентация по вкусовым товарам.
Презентация по вкусовым товарам. Предложение по проведению медиакампании для номинантов «Национальной Цифровой премии» «Золотой» пакет
Предложение по проведению медиакампании для номинантов «Национальной Цифровой премии» «Золотой» пакет Рембрандт Ван Рейн
Рембрандт Ван Рейн Выразительные возможности аппликации _Осенний листопад_. (2)
Выразительные возможности аппликации _Осенний листопад_. (2) Правописание безударных окончаний имен прилагательных единственного числа
Правописание безударных окончаний имен прилагательных единственного числа Никита Дубенцов1
Никита Дубенцов1 «ТЕХНОЛОГИЯ ПРОФЕССИОНАЛЬНОЙ КАРЬЕРЫ. ЭФФЕКТИВНОЕ ПОВЕДЕНИЕ НА РЫНКЕ ТРУДА»
«ТЕХНОЛОГИЯ ПРОФЕССИОНАЛЬНОЙ КАРЬЕРЫ. ЭФФЕКТИВНОЕ ПОВЕДЕНИЕ НА РЫНКЕ ТРУДА» Сказочный образ
Сказочный образ Діяльність НЕФКО в Україні. - презентация
Діяльність НЕФКО в Україні. - презентация