Теорема Пифагора и её применение

Цель: выявить причину неугасающего интереса к Пифагору и его теореме
Задачи:
изучить жизнь Пифагора
познакомить одноклассников с жизнью Пифагора
найти интересные способы доказательства теоремы
подобрать интересные задачи на применение теоремы
провести опрос родителей и старшеклассников о теореме и её использовании при решении задач
наметить пути решения подобной проблемы в стереометрии

План работы над проектом
Работа учащихся в группах:
Изучение биографии Пифагора
История теоремы и легенды о ней
Различные доказательства теоремы
Задачи на применение теоремы
Анкета «Что вы знаете о Пифагоре и его теореме?»

Анкета: Что вы знаете о Пифагоре
Кто такой Пифагор?
Когда и где жил Пифагор?
Что вы знаете о научной деятельности Пифагора?
Почему теорема носит его имя?
Какие легенды вы знаете о теореме?
Когда появились первые доказательства теоремы?
Как формулируется теорема?
Знаете ли вы доказательство теоремы?
Сколько существует доказательств?
Можете ли привести какое-нибудь?
Умеете ли применять теорему?
Применима ли теорема в других разделах геометрии?
Пригодилась ли теорема в вашей дальнейшей учёбе?

ПИФАГОР САМОССКИЙ
(ок. 570 – ок. 500 г. до н.э.)
О жизни Пифагора известно немного. Он родил-
ся в 580 г. до н.э. в Древней Греции на острове Самос,
который находится в Эгейском море у берегов Малой
Азии, поэтому его называют Пифагором Самосским.
Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в
то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отпра-
виться в Египет, где сам, когда-то изучал науки.

История теоремы Пифагора
Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия. Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». В связи с этим более правдоподобной можно считать следующую запись: «… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».
На протяжении последующих веков были найдены другие доказательства теоремы Пифагора. В настоящее время их насчитывается более ста.

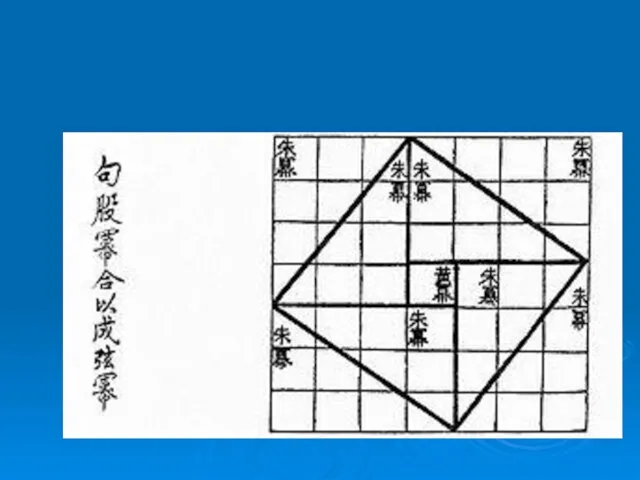
Одно из доказательств теоремы
В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели верёвок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Очень легко можно воспроизвести их способ построения. Возьмём верёвку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

Дружеские шаржи на теорему
Смотрите, а вот и "Пифагоровы штаны во все стороны равны"