Содержание
- 2. Исторический очерк XVI в. резко возрос объем работы ,связанный с вычислениями. Поэтому открытие логарифмов, сводящее умножение
- 3. Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Дж. Непером (1550—1617) и швейцарцем И.
- 4. Первые таблицы десятичных логарифмов (1617 г.) были составлены по совету Непера английским математиком Г. Бриггсом (1561
- 5. Непер Джон(1550—1617) —английский математик. Изобретатель логарифмов, составитель первой таблицы логарифмов,палочек Непера.
- 6. Логарифм -определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b.
- 7. Вещественный логарифм Логарифм вещественного числа logab имеет смысл при Логарифм: Комплексный логарифм
- 8. Наиболее широкое применение нашли следующие виды логарифмов: Натуральные: , основание: e (число Эйлера). Десятичные: , основание:
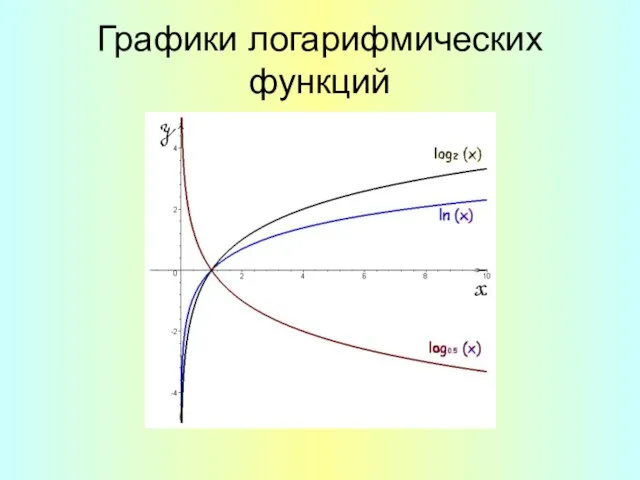
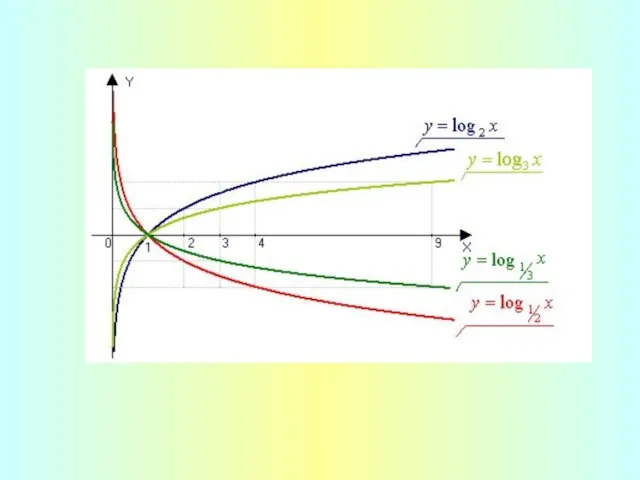
- 9. Графики логарифмических функций
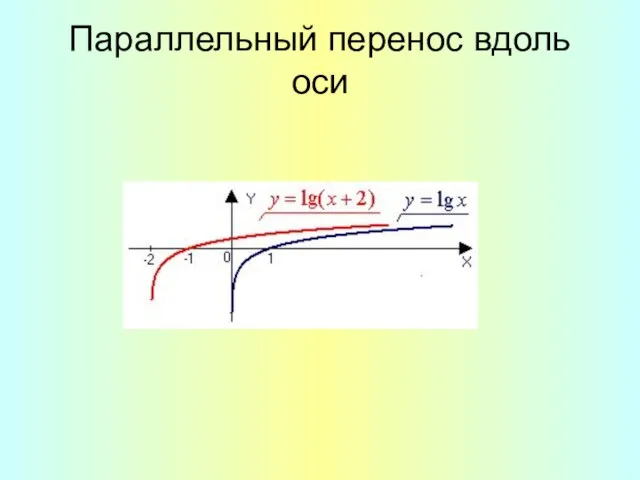
- 10. Параллельный перенос вдоль оси
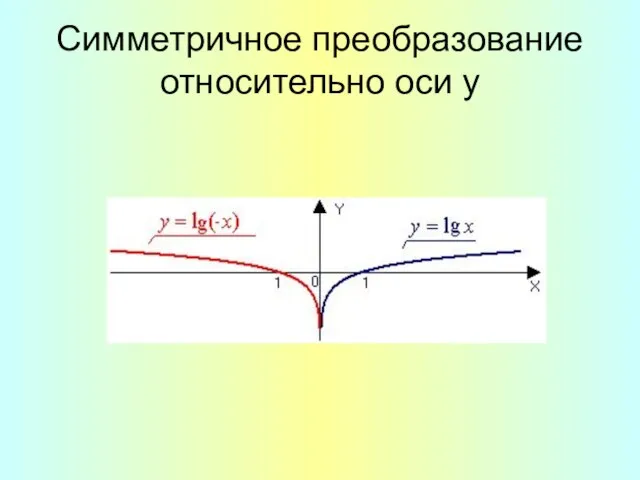
- 11. Симметричное преобразование относительно оси у
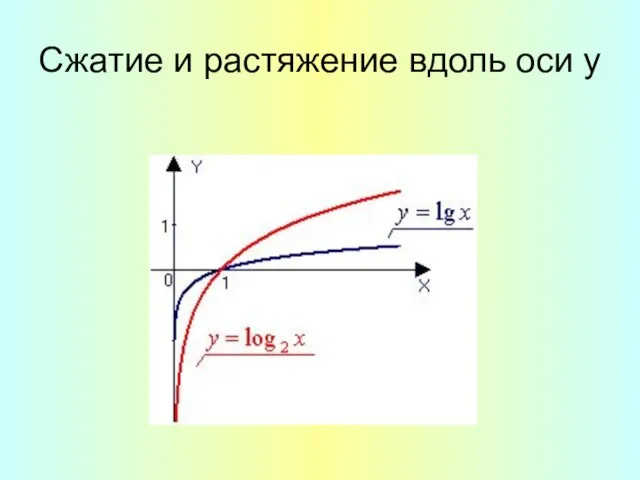
- 12. Сжатие и растяжение вдоль оси y
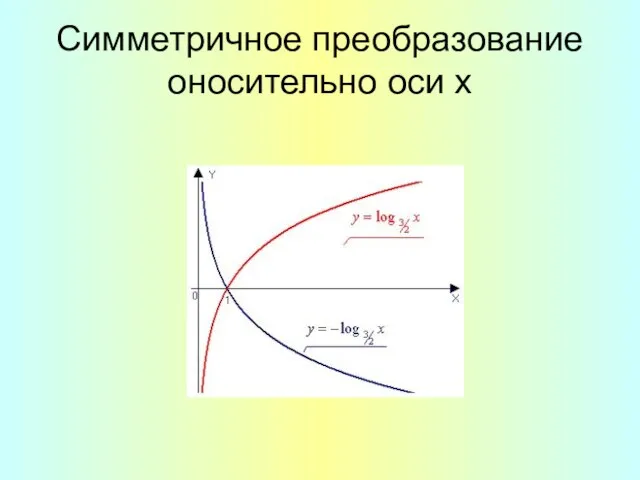
- 13. Симметричное преобразование оносительно оси х
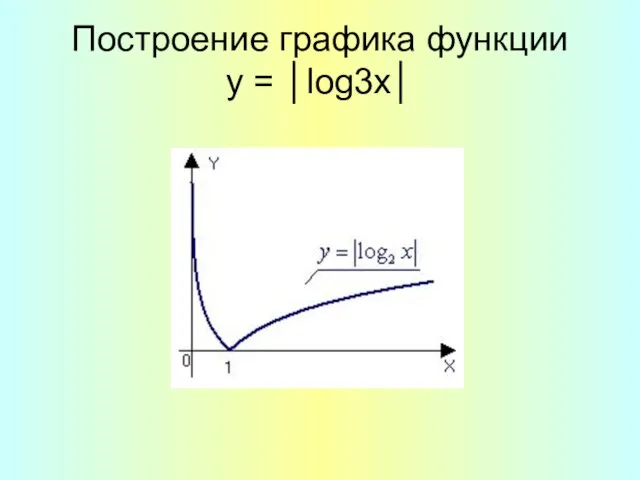
- 14. Построение графика функции y = │log3х│
- 16. Формула натурального логорифма:
- 17. Десятичные логарифмы Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений.
- 18. Логарифмическая функция Функция вида f(x) = logax, определённая при График любой логарифмической функции проходит через точку
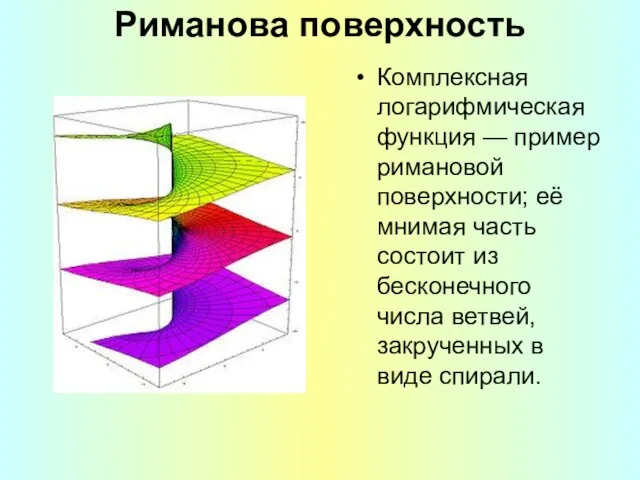
- 19. Риманова поверхность Комплексная логарифмическая функция — пример римановой поверхности; её мнимая часть состоит из бесконечного числа
- 20. Применение логарифма Астрономия-величина блеска звёзд
- 21. Логарифмическая спираль Форму логарифмической спирали имеют не только объекты астрономии, но и например: ракушки многих улиток,
- 22. Выводы: Логарифмической функцией называется функция вида f(x) = logax, определённая при
- 23. Свойства функции: Область определения (0; ) Область значений R Чётность /нечётность: функция не является ни четной,
- 24. Применение логарифмической функции Логарифмическая функция крайне важна в экономике, физике, при проведении научных, экспериментальных расчетов, астрономии
- 26. Скачать презентацию







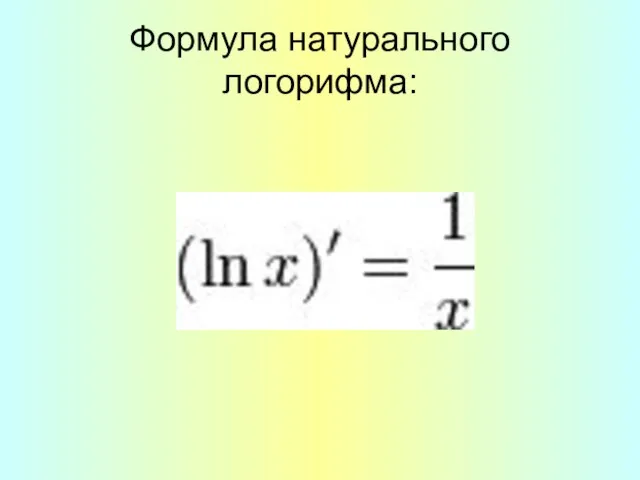







 Занятость и социальная защита населения
Занятость и социальная защита населения Дополнительный флакон с жидкостью от комаров на 45 ночей (без запаха) Эффективно уничтожает комаров в помещении в течение 45 ночей. В
Дополнительный флакон с жидкостью от комаров на 45 ночей (без запаха) Эффективно уничтожает комаров в помещении в течение 45 ночей. В 1929г
1929г ЧЕКАНКА ( тиснение по фольге)
ЧЕКАНКА ( тиснение по фольге) Тип Губки. Тип Кишечнополостные
Тип Губки. Тип Кишечнополостные Российские и международные гранты для молодых ученых:
Российские и международные гранты для молодых ученых: Основы философии
Основы философии Рейтинг надежности страховой компании: возможности и преимущества
Рейтинг надежности страховой компании: возможности и преимущества Командировка в восточное Оренбуржье
Командировка в восточное Оренбуржье Датчик
Датчик Копия Первые механизмы 4 года
Копия Первые механизмы 4 года Презентация на тему Советские деньги
Презентация на тему Советские деньги «О стратегии опережающего развития российской экономики в условиях глобальной нестабильности»19 марта 2012москва
«О стратегии опережающего развития российской экономики в условиях глобальной нестабильности»19 марта 2012москва Побег. Строение и значение
Побег. Строение и значение ОАО Туймазинский мясокомбинат
ОАО Туймазинский мясокомбинат Понятие о пищевых цепях и сетях. Экологические пирамиды
Понятие о пищевых цепях и сетях. Экологические пирамиды 1. Какой многоугольник называется правильным?
1. Какой многоугольник называется правильным? Организация системы управления предприятием ООО Автокрот+ в условиях неопределенности
Организация системы управления предприятием ООО Автокрот+ в условиях неопределенности Управление надежностью как инструмент достижения долгосрочных целей ОАО «ОГК-1»
Управление надежностью как инструмент достижения долгосрочных целей ОАО «ОГК-1» Монументальная скульптура и образ истории народа
Монументальная скульптура и образ истории народа Экслибрис. Виды экслибрисов
Экслибрис. Виды экслибрисов Анри Мари Раймон де Тулуз-Лотрек - французский живописец и график, один из ярчайших представителей постимпрессионизма
Анри Мари Раймон де Тулуз-Лотрек - французский живописец и график, один из ярчайших представителей постимпрессионизма НЕСТИ ДОБРО И РАДОСТЬ ДЕТЯМ!
НЕСТИ ДОБРО И РАДОСТЬ ДЕТЯМ! Программа обновления информации на сайте из файлов excel
Программа обновления информации на сайте из файлов excel ОМСКАЯ ОБЛАСТЬ
ОМСКАЯ ОБЛАСТЬ Оценка - aertalcream.ru
Оценка - aertalcream.ru Операції Європолу
Операції Європолу Языки программирования. Язык Паскаль.
Языки программирования. Язык Паскаль.