Содержание
- 3. Отгадайте ключевое слово урока 1) С ее появлением математика перешагнула из алгебры в математический анализ; 2)
- 4. Исторические сведения Производная – одно из фундаментальных понятий математики. Оно возникло в XV11 веке. Независимо друг
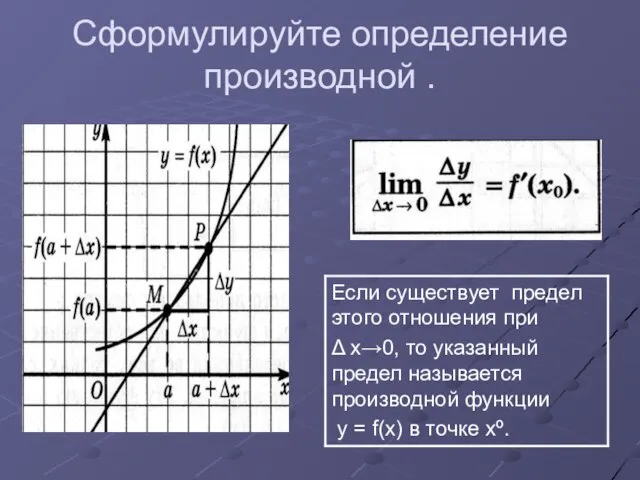
- 5. Сформулируйте определение производной .
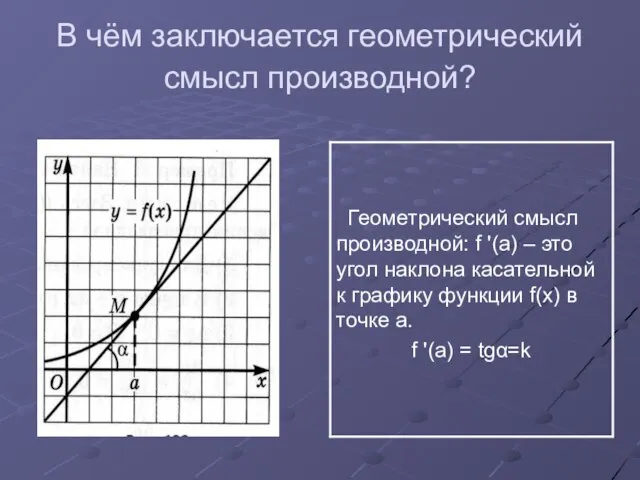
- 6. В чём заключается геометрический смысл производной?
- 7. Правила дифференцирования (u+v)' = u'+v' (ku)' = ku' (uv)' =u'v+uv' (u/v)' =(u'v-uv') / v²
- 8. Уравнение касательной
- 9. Алгоритм нахождения наименьшего и наибольшего значения функцииy=f(x) на отрезке [a; b] 1. Найдите производную. 2. Найдите
- 10. При исследовании свойств функции следует найти Область определения функции Производную Критические точки функции (производная равна 0
- 11. Найти производную
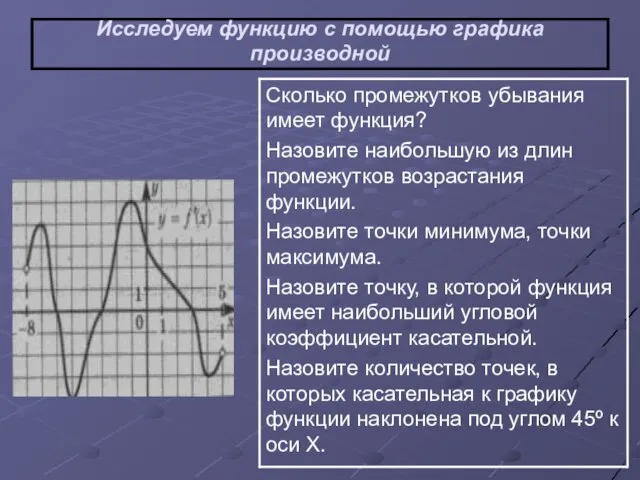
- 12. Исследуем функцию с помощью графика производной
- 13. «Что бы это значило?»
- 14. «Что бы это значило?»
- 15. Приложения производной Применении производной в геометрии(касательная к графику функции). Применении производной в физике и технике. Применение
- 16. Построение касательной и нормали к графику функции у = f(x) в точке Мٍ(а ٍ;f (аٍٍ))ٍ y
- 17. Групповая работа
- 18. Задание 1 группы Задача №1. Тело массой m кг движется по закону х(t) ( х –
- 19. Задание 2 группы Составить уравнение общих касательных к кривым f(x)=х² +4х +8 и g(x) = х²
- 20. «Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы: движение». Ф.Энгельс
- 21. Задание для всех групп Что вы можете сказать о производной функции, которую описывает поговорка «Чем дальше
- 23. Скачать презентацию





![Алгоритм нахождения наименьшего и наибольшего значения функцииy=f(x) на отрезке [a; b] 1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/469026/slide-8.jpg)











 Правонарушения в среде несовершеннолетних
Правонарушения в среде несовершеннолетних портфолио учителя начальных классов МБОУ СОШ №12 Сеногноевой Елены Александровны
портфолио учителя начальных классов МБОУ СОШ №12 Сеногноевой Елены Александровны Типы алгоритмов.
Типы алгоритмов. «Оккупационные деньги»
«Оккупационные деньги» МИРОВАЯ ЭКОНОМИКА начала 21 века
МИРОВАЯ ЭКОНОМИКА начала 21 века Семейный фотоальбом или история компьютерной мышки
Семейный фотоальбом или история компьютерной мышки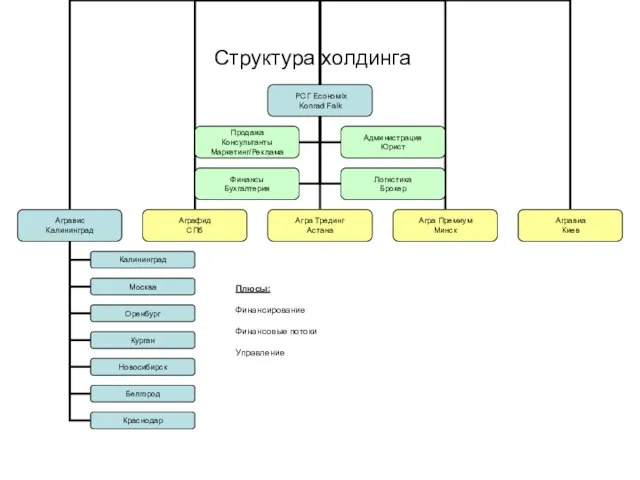 Структура холдинга
Структура холдинга Философия проекта Fc Goodness
Философия проекта Fc Goodness 1711-2011
1711-2011 Сложное дополнение (Complex Object)
Сложное дополнение (Complex Object) Как работать над лингвистическим сочинением?
Как работать над лингвистическим сочинением? Достопримечательности стран мира
Достопримечательности стран мира  Урок русского языка в 1-м классе по теме: "Слова с сочетаниями "жи, ши"
Урок русского языка в 1-м классе по теме: "Слова с сочетаниями "жи, ши" Образовательная политика в России. Принципы государственной политики в образовании
Образовательная политика в России. Принципы государственной политики в образовании Müzi̇k ve güzel sanatlar ensti̇tüsü
Müzi̇k ve güzel sanatlar ensti̇tüsü Унификация учетных процедур и создание цифровой среды учетных данных
Унификация учетных процедур и создание цифровой среды учетных данных Собака – друг человека
Собака – друг человека Установка на проектно-аналитическую сессию №4
Установка на проектно-аналитическую сессию №4 The shops of the world
The shops of the world Рынок денег. Банковская система. Тема 7
Рынок денег. Банковская система. Тема 7 Горные породы 5 класс
Горные породы 5 класс Зимующие птицы хутора Добринка
Зимующие птицы хутора Добринка Интерактивные методы обучения
Интерактивные методы обучения Управление материальными и информационными потоками
Управление материальными и информационными потоками Системы бизнес-планирования
Системы бизнес-планирования Область применения печатных плат с металлическим основанием
Область применения печатных плат с металлическим основанием Теорема Виета
Теорема Виета Роль МИ в принятии управленческих решений
Роль МИ в принятии управленческих решений